2018年全国数学高考卷Ⅰ文科第21题探究*

●

(宿城第一中学,安徽 宿州 234000)

1 试题展现

例1已知函数f(x)=aex-lnx-1．

1)设x=2是f(x)的极值点，求a，并求f(x)的单调区间；

(2018年全国数学高考卷Ⅰ文科试题第21题)

点评本题是2018年全国数学高考卷Ⅰ文科试题的压轴题.试题的命制严格遵循《普通高中数学课程标准(2017年版)》《2018年普通高等学校招生全国统一考试大纲》《2018年普通高等学校招生全国统一考试说明》(以下分别简称《课程标准》《考试大纲》《考试说明》)的要求，体现了素养导向，展现了数学的科学价值和人文价值，同时兼顾试题的基础性、综合性和应用性．第1)小题考查导数极值的判断、单调区间的求法，注重基础，学生容易得分；第2)小题注重对学生能力的考查，以不等式证明为载体，考查学生灵活运用导数知识分析问题、解决问题的能力,有一定的广度和深度，入口较宽，解法多样，有利于对学生进行多层次、多角度的考查，作为压轴题起到了把关作用．

2 解法探究

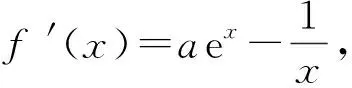
下面对第2)小题进行探讨.

2.1 分离参数,转化化归

从而φ(x)在(0,+∞)上单调递减，又φ(1)=0，于是当x∈(0,1)时,φ(x)>0，故h′(x)>0，h(x)单调递增；当x∈(1,+∞)时,φ(x)<0，故h′(x)<0，h(x)单调递减，因此

故

2.2 带参求导,设而不求

证法2由f(x)=aex-lnx-1，知

从而f′(x)在(0,+∞)上单调递增.因为

f′(1)=ae-1≥0，

又

f(x)min=f(x0)=aex0-lnx0-1.

lna+x0=-lnx0，

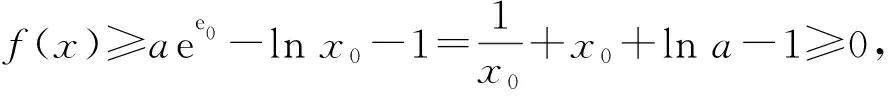
2.3 参数放缩,巧解问题

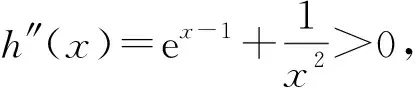
h(x)min=h(1)=0，

故

h(x)≥0．

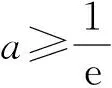
2.4 变量放缩,分类讨论

证法4记φ(x)=x-1-lnx(其中x>0)，则

从而当x∈(0,1)时，φ′(x)<0，φ(x)单调递减；当x∈(1,+∞)时，φ′(x)>0，φ(x)单调递增，于是

φ(x)min=φ(1)=0，

因此

φ(x)≥0，

故当x>0时，x-1≥lnx,即欲证aex-lnx-1≥0，只需证aex-x≥0.记h(x)=aex-x，则

h′(x)=aex-1，

令h′(x)=aex-1=0，即

②当a>1时，h′(x)>0，从而

h(x)>h(0)=a>0,

得证．

点评证法4是对变量进行放缩，根据“当x>0时，x-1≥lnx”把要证明的不等式转化为证明其成立的充分条件“aex-x≥0”，然后对a进行分类讨论，进而原不等式得证．证法4虽很繁冗，但是把解题思路打开了，给后面的方法提供了更多思考的空间，要证明不等式，根据分析法可以证明使它成立的充分条件成立．

2.5 参变同缩,“秒杀”问题

证法5记h(x)=ex-1-x(其中x>0),则

h′(x)=ex-1-1，

从而h(x)在(0,1)上单调递减，在(1,+∞)上单调递增，进而

h(x)≥h(1)=0，

于是当x>0时，ex-1≥x，两边取自然对数可得

x-1≥lnx．

因此aex-lnx-1≥ ex-1-lnx-1≥

x-(x-1)-1=0，

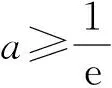
3 追本溯源,揭示本质

3.1 几何视角

3.2 代数视角

泰勒公式：f(x)=ex在x=0处的泰勒展开式为

即

因此

ex≥x+1[1].

用x-1代换不等式ex≥x+1中的x，可得ex-1≥x.当x>0时，对ex-1≥x两边取自然对数可得

x-1≥lnx，

从而

ex-1≥1+lnx，

即

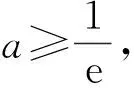
从代数的角度来理解试题命制的本源，结合几何的感性直观，有利于建立形与数的联系，提高直观想象能力，培养学生的数学核心素养,有利于从广度和深度两个层次对问题进行理解和剖析．

3.3 同源探究

例1与2013年全国数学高考卷Ⅱ理科试题第21题(例2)同根同源.

例2[1]已知函数f(x)=ex-ln(x+m)．

1)设x=0是f(x)的极值点，求m，并讨论f(x)的单调区间；

2)当m≤2时，证明:f(x)>0．

首先从试题形式来看,两者相似度极高;再从解题方法看，在例2第2)小题中证明f(x)>0，可以使用:

①参数放缩，只需证

ex-ln(x+2)>0，

借助设而不求，不等式得证，参见例1第2)小题的证法3；

②参变同时放缩，只需证

ex≥x+1≥ln(x+2)，

从代数、几何视角均可证明，又因两个等号不同时成立，不等式得证，参见例1第2)小题的证法5．

4 解后反思

4.1 重视教材,抓“四基”

《课程标准》要求通过高中数学课程的学习，学生能获得进一步学习以及未来发展所必需的“四基”(数学基础知识、基本技能、基本思想、基本活动经验)．《课程标准》是教材编制的依据，教材是课程标准的具体体现．抓“四基”，就要重视教材．例1植根于教材，在《数学(必修1)》对数函数的图像与性质中，明确要求学生了解同底的指数函数和对数函数互为反函数，图像关于y=x对称，在2018年的《考试大纲》中也有要求．学生扎实的“四基”是分析问题的根基,是解决问题的保障，因此高三复习要重视教材．重视教材不是把学过的教材拿过来重新学一遍，而是要对教材进行挖掘，科学整合教材中的例题、习题，发挥教材的最大效益．

4.2 高于教材,抓“四能”

高三复习中“四基”固然重要，但也不能仅局限于教材，故步自封，忽视学生的认知和发展规律．通过高中课程的学习还要构建(提高)学生的“四能”(从数学角度发现和提出问题的能力、分析和解决问题的能力)．“四基”是知识的内化于心，“四能”是知识的外化于行．“四能”的培养需要根据最近发展区理论，创设高于教材的教学内容．新高考强调以数学知识为载体，从问题入手，考查学生的个体理性思维的广度和深度以及进一步学习的潜能．例1考查由指数函数y=ex与对数函数y=lnx平移之后的指数、对数型函数，这样的函数源于教材，但又高于教材要求．因此要提高“四能”，就要在高三复习时，适切讲授高于教材的知识，比如常见的泰勒展开式、洛必达法则、拉格朗日中值定理等，既能拓宽学生的知识面，又可以开阔学生的解题视野．

4.3 关注素养,抓“创新”

2018年的高考命题强调以素养为导向，考查学生创造性的探究能力．《考试大纲》要求：对创新意识的考查是对高层次理性思维的考查，在考试中创设新颖的问题情境，构造有一定深度和广度的数学问题时，要注重问题的多样化，体现思维的发散性；精心设计考查数学主体内容、体现数学素质的试题；也要有反映数、形运动变化的试题以及研究型、探索型、开放型等类型的试题．例1考查学生直观想象、逻辑推理、数学运算等数学核心素养，是对学生创新意识和能力考查的最好体现．苏霍姆林斯基说过：“在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者、探索者．”因此在高三复习中，教师更应关注学生数学核心素养的提升，狠抓创新教育，让学生能以一个发现者、研究者、探索者的身份引领新时代创新的发展．