技法诚可贵 思想价更高*——2018年浙江省数学高考第8题解析

●

(温州市第十四高级中学，浙江 温州 325000)

2018年的浙江高考落下帷幕，一年一度的高考题总会引起一线教师的关注、研究，各种解法琳琅满目.但是作为教师应清醒地认识到解题技法固然重要，但解题思想更为重要.正所谓“技法诚可贵、思想价更高”，解题只有探源思想，解法才能源源不断地浮现.笔者以2018年浙江省数学高考第8题为例，和大家分享从解法探究到思想探源，再纵向联系浙江历年高考中类似的试题，并在此基础上总结基于学科核心素养的教学启示，欢迎同行批评指正.

1 高考真题

例1已知四棱锥S-ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点(不含端点)，设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3，则

( )

A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1

C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1

(2018年浙江省数学高考试题第8题)

这是一道考查空间角(线线角、线面角、二面角)的小题，反映了在点、线、面动态变化过程中的空间角大小顺序的不变性,以能力立意，切入口宽，内涵丰富，值得研究.

2 解法探究

我们常常发现教师苦口婆心地介绍一题多解，然而学生除了崇拜似乎很难学会，究其原因是只讲技法，没有思想.于是解题方法变成了“无根之水”，方法越多越糊涂，这是值得我们深思的.因此，解法探究的核心是解题思想的提炼.

2.1 解析思想——建立函数模型

分析本题中四棱锥是动态的，对每一个给定的四棱锥，棱AB上的点E也是动态的，对于动态的量我们最先想到是借助什么工具来描述呢？自然想到空间直角坐标系的解析思想.

图1

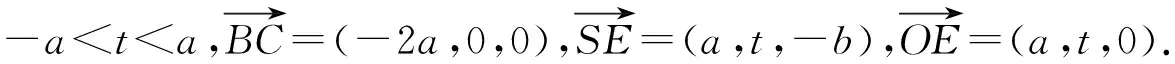
因为cosθ1≤cosθ3,又

所以

cosθ3≤cosθ2.

综上可知，cosθ1≤cosθ3≤cosθ2,即θ2≤θ3≤θ1.

2.2 数形结合思想——数学直观

分析对于动态对象的描述，除了解析表示外还能从几何直观方面加以考虑吗？引导学生思考：动点成线，动线成面，动面成体.本题要比较的对象是什么？关于这些空间角你知道哪些性质？启发学生注意线面角的最小性、二面角的最大性.此外，要比较大小，还要关注变化中的不变量.基于以上思考，得到如下解法：

解法2当点E在棱AB上运动时，SE的轨迹是平面SAB的一部分，根据二面角的最大性，知θ2≤θ3.如图2，记棱AB中点为E0，O为底面中心，易知BC∥OE0，故二面角θ3即为BC与平面SAB所成角，而SE是平面SAB内的一条线，根据线面角的最小性，知θ3≤θ1.综上所述,θ2≤θ3≤θ1.

直观想象是数学的六大核心素养之一，笔者猜测解法2可能是本题的立意——数学是直观的、数学是好玩的、数学也是深刻的.只有看透本质，方能凸显实质.

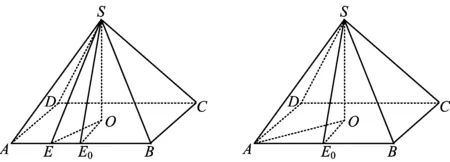
图2 图3

2.3 特殊化思想——数学直觉

分析如图3，如果对于动态问题把握不好，是否可以充分利用选择题的特点，化动态为静态呢？因为结果都反映了动态变化中的角度大小顺序的相对不变性，所以可以特殊化正四棱锥，还可以特殊化点E的位置，于是形成下面的解法.

解法3将正四棱锥特殊为所有棱长均相等的正四棱锥，将点E无限接近于端点A，则易知

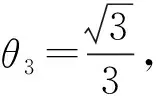
θ2≤θ3≤θ1.

有些师生对特殊化思想存在误解，感觉纯属投机，实则不然.这一思想的背后包含着合情推理、逻辑论证、转化化归，乃至辩证分析的综合素养，也反映了学生看待数学问题的眼光和思维方式.但命题者似乎并不希望学生用特殊法，故意表明不含端点，意在告诉学生此法有风险，后果自负.但是只要有极限思想的学生，照样可以取端点，从而获得结果.

追寻向量思想、竞赛化思想，还能发现基向量分解、三面角公式等不同解法，在进行解法探究的时候，应该基于学科核心素养帮助学生形成解题思想.“问渠哪得清如许，为有源头活水来”，源源不断的解法好比是“术”，而背后的解题思想就是“道”，只有悟“道”之“术”，方能应对高考，笔者认为这也是浙江高考卷希望传达的信息之一.笔者继续探源思想，发现本题实际上是考查空间角的概念、空间问题的降维思想，也蕴含着传播数学文化的意向，展现了“平凡中见神奇”的成效.

3 思想探源

3.1 考查空间角概念，彰显降维思想

本题将空间中的3个角放在一起考查，足见命题者的良苦用心.笔者猜想命题者希望传达“回归教材，重视概念”的强烈信息.根据空间角概念，所有空间角最后都降维成线线角，因此只要在正四棱锥内作出θ1,θ2,θ3即可.于是又得一解法.

解法4如图4，记E0为棱AB的中点，顶点S在底面的射影为O(易知O为底面正方形的中心)，过点O作OO1∥AB，过点E作EO1∥E0O，则易证EO1⊥SO1.联结SE，SE0,则

∠SEO1=θ1, ∠SEO=θ2, ∠SE0O=θ3,

从而

于是

θ1≥θ3,

又

即

θ3≥θ2,

综上可知，θ2≤θ3≤θ1.

“看似平凡最崎岖，成如容易却艰辛”,笔者认为解法4看似平常，却是凸显本质的解法.

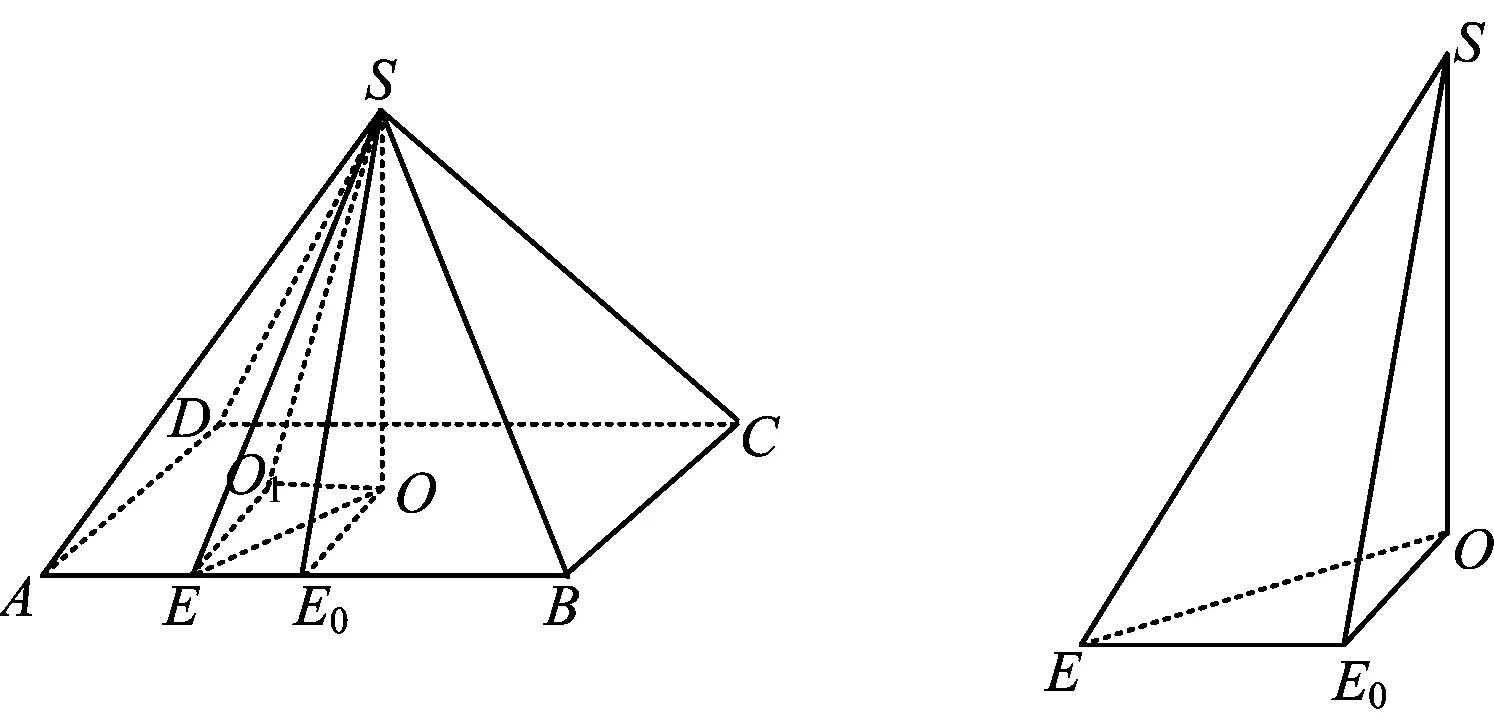
图4 图5

3.2 传播数学文化，追求文化育人

笔者还发现，例1的3个空间角θ1,θ2,θ3分别是图5中异面直线SE,OE0所成的角、SE与平面EOE0所成的线面角、二面角S-EE0-O.

题目中的3个空间角恰好包含在一个4个面均为直角三角形的三棱锥内，这种几何体在中国古代称为三角锥体，又称鳖臑.命题者通过本题巧妙而委婉地表达了对数学文化的关注与传播，真可谓“用心良苦”！

4 高考链接

笔者进一步查阅近几年浙江省数学高考题，发现“空间角”是浙江省数学高考的常考内容.而且从2014年开始基本是考查动态变化中角的大小比较或最值问题，但3个空间角一起考查，2018年尚属首次.下面让我们纵向联系、细细品味近几年高考中类似的试题，正所谓“横看成岭侧成峰”，换个角度看问题，相信会有意外收获.

( )

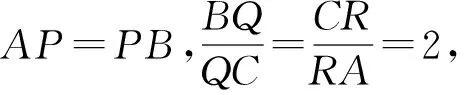
A．γ<α<βB．α<γ<β

C．α<β<γD．β<γ<α

(2017年浙江省数学高考试题第9题)

答案B.

点评考查形式与例1相似，都是考查变化过程中角的大小相对不变性.确定和变化是相对的，面对变化的问题需要在变化中寻求不变量.比如3个二面角的高就是相对确定的，考生只要掌握二面角的概念和立体几何中的降维思想，就可以转化为△ABC中心O到PQ,PR,RQ的距离比较.

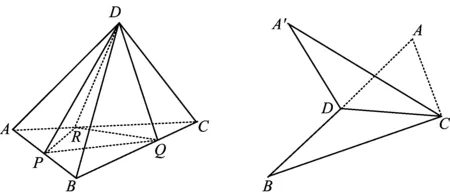
图6 图7

例3如图7，已知△ABC，D是AB的中点，沿直线CD将△ACD翻折成△A′CD，所成二面角A′-CD-B的平面角为α，则

( )

A．∠A′DB≤αB．∠A′DB≥α

C．∠A′CB≤αD．∠A′CB≥α

(2015年浙江省数学高考理科试题第8题)

答案B.

点评本题考查折叠过程中的线线角与二面角的大小相对不变性，形式与例1、例2大致相似.本题解法多样，可以将空间角转化为平面角，通过解三角形、余弦定理比较角的余弦值;也可以用特殊位置法解决；还可以转化为求直线A′A与平面ABC所成角的大小和直线A′A与平面ABC内的直线BD所成角的大小比较，其实质是线面角的最小性.

图8

例4如图8，某人在垂直于水平底面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面的射线CM移动，此人为了准确瞄准目标点P，需要计算由点A观察点P的仰角θ的大小.若AB=15 m,AC=25 m,∠BCM=30°,则tanθ的最大值为______(仰角θ为直线AP与平面ABC所成角).

(2014年浙江省数学高考理科试题第17题)

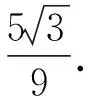
点评这是一道动态变化中角的最值问题.本题解法也不唯一，比较典型的有两大类：一类是函数思想，关键是寻找自变量，比如可以先作出线面角θ，将tanθ表示为以CQ为变量(点Q为点P在平面ABC的射影)的函数，再求出最大值.还有一类是动态分析、数学直观想象——动点成线，动线成面，直线AP与平面ABC所成角的最大值即是二面角M-AC-B的大小，即二面角的最大性.

仔细品味发现近几年浙江省数学高考关于“空间角”的试题存在千丝万缕的关系，都关注空间角的概念，关注空间角转化为平面角的降维思想，都注重能力立意，渗透素养考查；关注函数思想，凸显数学直观.尽管现在看来似乎是“事后诸葛”，但为我们指明了如何备考复习的一条路径——数学教师要善于研题，尤其是研究高考题.研题既是高中数学教师必备的素养与能力，也是教学研究的重要组成部分.研题的最终目的是为了学生的学，帮助学生走出题海，提高效率，减轻学生的学习负担.

5 教学启示

5.1 回归教材，重视概念教学

曾几何时，数学课堂中经常找不到数学课本了，抽屉里充斥着各种教辅用书，师生遨游在茫茫题海中.高中数学课堂教学渐渐演变为“题型教学”，题型教学又进一步蜕化为“刺激—反应”训练的状况[1].笔者认为2018年的高考题比较清晰地传达了回归教材、重视概念教学的信息，笔者统计了一下，2018年的浙江卷除了第8题，还有第7，18，20等题也体现了类似的命题意图.

基于数学学科核心素养，回归教材，重视概念教学，如何把知识的学术形态转化为教育形态？如何挖掘数学内部资源实现数学的育人？是值得每一位数学教育工作者不懈探究的课题.

5.2 解题教学要关注解题思想

数学离不开解题，考试更离不开解题，但缺乏解题思想引领的解题技法应当摒弃，就好比失“道”之“术”，容易走火入魔；也正如萤火虫，有耀终非火.而且，这种解题教学并非只用于高三复习阶段，更应该内化于每一节新课教学中.

5.3 数学教学也要关注文化育人

浙江师范大学张维忠教授一直强调数学教师要有文化情怀，呼吁：以文化情怀去教学，做数学文化的传播者[3].既传播我国古代数学文化，激发民族自豪感，也能通过学习发现数学的和谐美、对称美、简洁美，还能培养从直观猜想到严格论证的数学理性精神，实现数学地育人.事实上，那些值得学生终身追忆，给学生留下深刻印象，真正开启学生心智的事件，往往发生在偏离主题的云游中[4].

6 结语

如果说高考是“指挥棒”，那么笔者对2018年浙江省数学高考第8题的解析表达了对解题研究的观点,技法诚可贵，思想价更高.而解题思想的培育又指向了基于核心素养的课堂教学，因此“回归教材，重视概念教学，关注数学育人”也是2018年浙江高考卷对课堂教学的“指挥导向”.