穿插故事情节 生动数学课堂*——将数学课堂“故事化”的初探

●

(太湖高级中学,江苏 无锡 214125)

数学是研究空间形式和数量关系的科学，是刻画自然规律和社会规律的科学语言和有效工具，是一门逻辑性较强的自然科学.由于高中数学知识概念抽象、思维要求高、习题类型多、解题技巧灵活多变、计算复杂等原因，导致部分学生学习数学的热情不高.为了改变这种状况，寻找可突破的途径，笔者做了大胆的尝试，在课堂教学中穿插故事情节，激发学生学习数学的兴趣[1].在观看电影时，生动的故事情节往往能使我们产生强烈的好奇心，让我们全神贯注，当我们回忆的时候，很多情节都能记忆犹新.如果教师的课堂教学也有此属性，那么学生定能对数学学习充满兴趣.现以“极大值与极小值”为例撰写成文，与同行交流.

1 故事情节构思

1)故事的设想是：在教师的带领下，全体学生向新知领域前进，在探索的过程中定会遇到艰难险阻，需细心谨慎，迎难而上，才能突破重重阻碍，到达成功的彼岸.

2)故事的情节发展的关键词：①回首：回首瞭望所走过的路(复习旧知)；②撤步：从所熟悉的地方(知识)出发；③前行：遇见新东西(新知)；④慢步：走慢一些，观察了解周围的环境(感悟新知)；⑤遇水：前行过程中遇到了险阻(困难)；⑥轻舟：为了成功到达彼岸，必须制造渡河工具(求函数极值的方法)；⑦击水：有了渡河工具，便可去中流击水(掌握函数极值的求法)；⑧逐浪：在击水过程中，遇到风浪当迎难而上(掌握“f′(x0)=0”与“f(x0)是函数的极值”之间的关系)；⑨破浪：冲破险阻(运用知识解决问题)；⑩弄潮：顺利到达成功的彼岸，让学生谈谈本节课的收获.

2 教学流程简介

2.1 回首

师：同学们，上节课我们利用导数来研究函数的单调性问题，请大家回顾一下：用导数求函数y=f(x)单调递增区间的基本步骤是什么？

生1：1)明确函数的定义域；2)求出导函数f′(x)；3)解不等式f′(x)>0；4)由函数定义域与不等式f′(x)>0解集的交集，可得函数的单调递增区间.

师：很好！同样，令导函数f′(x)<0，由函数定义域与不等式f′(x)<0解集的交集，可求出函数的单调减区间.

2.2 撤步

生2：先求函数f(x)的导函数f′(x)=x2-1，再令f′(x)>0，得x<-1或x>1，因此该函数的增区间为(-∞,-1)，(1,+∞)，同理可得该函数的减区间为(-1,1).

师：很好！请大家思考，当自变量x变化时，函数值y是怎样变化的？

(教师通过投影展示学生所作图像，如图1).

生3：当x∈(-∞,-1)时，y随x的增大而增大；当x∈(-1,1)时，y随x的增大而减小；当x∈(1,+∞)时，y随x的增大而增大.

图1

师：很好！从函数单调性的变化情况来看，自变量x在哪些位置是特殊的？

生4：当自变量x=±1时，可能有些特殊.

师：请你说说当自变量x=-1时，为什么是特殊的？

生5：函数f(x)在x=-1的左侧是单调递增的，在x=-1的右侧是单调递减的，故x=-1是函数f(x)单调性的分界点.

师：“分界点”这一词说得很好.还有其他看法吗？

生6：它是函数单调性的转折点，在这一点函数的单调性出现反转，由递增变递减.

师：“转折点”这一词说得也很好，两位同学都是从“形”的角度思考的，能否从“数”的角度思考呢？

生7：这一点的函数值比它附近点的函数值都大.

师：是函数的最大值吗？

生8：不是.

师：那是什么呢？这就是我们今天学习的新知识——极大值.本节课我们主要来研究可导函数的极大值与极小值.

苏教版《数学(选修1-2)》第76页明确指出：如无特殊说明，本章所涉及的函数都是可导函数.

2.3 前行

图2

师：结合图2，谁能给出极大值的定义呢？

生9：函数在点P处从左侧到右侧由“上升”变为“下降”，这时在点P附近，点P的位置最高，也就是说f(x1)比它附近点的函数值都要大，可称f(x1)为函数f(x)的一个极大值.

师：谁能给出极小值的定义呢？

生10：函数在点Q处从左侧到右侧由“下降”变为“上升”，这时在点Q附近，点Q的位置最低，也就是说f(x2)比它附近点的函数值都要小，可称f(x2)为函数f(x)的一个极小值.

师：函数的极大值与极小值统称为函数的极值.

2.4 慢步

图3

师：如图3，观察函数f(x)的图像，请你说出图中的极大值和极小值.

生11：极大值是f(x1)与f(x3)，极小值是f(x2)与f(x4).

师：可见函数f(x)的极大值(极小值)不一定是唯一的，函数f(x)的极大值一定大于它的极小值吗？

生12：不一定，由图3可知极大值f(x1)小于极小值f(x4).

师：由此可见，一个函数的极大值与它的极小值之间没有必然的大小关系.这是因为极值是一个局部的概念.

2.5 遇水

师：前面我们研究了函数单调性与导数值的正负之间的关系，现在请大家思考函数极值与导数值之间又有什么关系呢？

生13：由图3可知，若f(x1)为函数f(x)的一个极大值，则f′(x1)=0;若f(x2)为函数f(x)的一个极小值，则f′(x2)=0.

师：为什么呢？

生14：因为x1的左侧函数递增，导数值为正，右侧递减，导数值为负，导数值由正到负，故f′(x1)=0.

师：很好！还有其他的解释吗？

生15：因为在x=x1处切线平行于x轴，其斜率为0，故f′(x1)=0.

师：很好！同样，在x2的左侧函数递减，导数值为负，右侧递增，导数值为正，导数值由负到正，故f′(x2)=0.你能用自己的语言总结一下函数极值与导数值之间的关系吗？

生16：如果f′(x0)=0，且在x0的两侧导数值为左正右负时，那么f(x0)是函数的极大值；如果f′(x0)=0，且在x0的两侧导数值为左负右正时，那么f(x0)是函数的极小值.

师：很好，可简记为口诀：左正右负，函数取得极大值；左负右正，函数取得极小值.

2.6 轻舟

师：如何求函数y=f(x)(其中x∈(a,b))的极值？

生17：1)先求方程f′(x)=0的根x0∈(a,b)；2)再利用口诀求极值.

2.7 击水

例1求函数f(x)=x2-x-2的极值.

师：请大家思考例1.

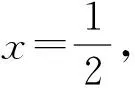
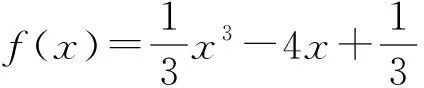
2.8 逐浪

师：由以上可知，若f(x0)是函数f(x)的极值，则必须满足两个条件：1)f′(x0)=0；2)在x0的左右两侧导数值是异号的.问：若f′(x0)=0，则f(x)在x0处一定取得极值吗？

生20：不一定！如函数f(x)=x3，其导函数为f′(x)=3x2，在x=0处导数值为0，但其左右两侧导数值均为正，显然f(0)不是函数y=x3的极值.

师：那么“f′(x0)=0”是“f(x0)是函数f(x)的极值”的什么条件？

生21：必要不充分条件.

师：事实上这样的函数太多啦，形如f(x)=ax3(其中a≠0)，其导函数为f′(x)=3ax2.当a>0时，在x=0左右两侧导数值均为正；当a<0时，在x=0左右两侧导数值均为负，因此f(0)不是函数y=ax3的极值.

2.9 破浪

师：请大家思考例3.

例3已知函数f(x)=x3-ax2-bx+a2在x=1处有极值为10，求实数a，b的值.

生22：因为f′(x)=3x2-2ax-b，由题意可得

代入得

从而

a2-a-(3-a)-9=0,

即

a2+a-12=0，

解得a=3或a=-4.因此当a=3时，b=-3；当a=-4时，b=11.

师：对此结果大家有何看法？

生23：要检验.

师：为什么？

生24：由f′(1)=0不一定能得到函数在x=1处有极值.

师：很好，因此要增加检验环节.当a=3，b=-3时，f′(x)=3x2-6x+3=3(x-1)2，在x=1的左右两侧导数值同正，因此在x=1处无极值，舍去；当a=-4，b=11时，

f′(x)=3x2+8x-11=(x-1)(3x+11)，

此时在x=1的左右两侧导数值是异号的，符合题意.

综上可知：a=-4，b=11.

2.10 弄潮

师：通过本课的学习，谈谈你的收获.

生(众)：一方面掌握了求函数的极大值与极小值的方法；另一方面，从“回首→撤步→前行→慢步→遇水→轻舟→击水→逐浪→破浪→弄潮”这些环节感受到了一个故事：当一个人在未知领域中探索、前进时，肯定会遇到一些困难，面对困难，我们要迎难而上，寻求解决困难的方法，树立信心，最终定能取得成功.

师：总结得很好！

3 教学体会

新学期开学后笔者任教高二文科班的数学，学生对数学学习普遍缺乏信心和兴趣，导致学生成绩不够理想，课堂教学氛围比较沉闷.为了激发学生的兴趣，笔者在课堂教学中实施穿插故事情节，通过两个多月的实践，课堂教学面貌发生较大变化，教学体会如下：

3.1 穿插故事情节，能使学生学习兴趣更高

为了更好地展现故事情节，可在每张幻灯片的关键词旁边适当配置一张紧扣主题的图片，这样可让学生更有画面感，使学生在上课时能感受到故事情节在一幕幕的推进，从而激发了学生的好奇心，使学生对数学学习产生了浓厚的兴趣，上课时学生的注意力更集中，目光更有神，坐姿更端正，回答问题的声音更响亮.每当显示出下一张幻灯片的时候，总能吸引学生的目光，激发学生对问题的思考.

3.2 穿插故事情节，能使教师教学效果更好

对于数学基础薄弱的学生，因学习成绩不够理想，从而对自己的能力产生消极的认识，学习兴趣不足，学习的情绪和行为变得消极，成绩不够理想,进入一个恶性循环的怪圈.在课堂教学中实施穿插故事情节以后，正是在这个恶性循环的怪圈中打开了一个缺口，让学生体验到课堂的乐趣，学习的热情逐渐提高，开始愿意与教师互动，或与自己周围的学生交流，学生的课堂参与度显著提升，形成良好的课堂氛围[2].由于故事情节与教学内容的交织，使教学内容结构清楚,层次分明.关键词对每一部分知识具有点题的作用，使学生更容易理解每一部分知识，且便于记忆.通过长期练习，学生已经知道关键词可以连成一个故事，只要记住故事情节就可以记住课堂所学内容，因此当学生回顾课堂所学内容时，学生已能像讲个故事一样，将本课堂的知识娓娓道来，课堂教学效果得到显著提高.

3.3 穿插故事情节，能使数学课堂意境更深

为了让学生更能投入课堂，故事情节的设置应有所选择[3].人的内心都对真理充满渴望，对真理的寻找是不会停止的.若能让学生在数学课堂接受新知的同时，从所穿插的故事中领悟一番人生道理，数学教学的育人功能就能得到充分体现.本课设计的故事包含学生探索、求知的心路历程，为了让学生体验到数学课堂的意境美，可以考虑在每张幻灯片的标题栏写一个具有诗意的关键词，或者写一句诗词，用来给数学课堂增添诗情画意，意义深远.关键词“轻舟”出自李白的《早发白帝城》，“击水”出自毛泽东的《沁园春·长沙》，“破浪”出自李白的《行路难·其一》等.数学源于自然，有自然的美，本身也是诗，因此在数学教学中可以通过“诗化”，让学生的数学学习充满诗情画意.