基于目标意识 回归本原问题*

●

(南京师范大学附属扬子中学,江苏 南京 210048)

高三解题教学的首要任务是教会学生如何解题，进而提升学生的数学素养.实践表明，要使学生真正学会解题，需从数学本质出发，深究解题策略.常规的解题是按照由条件出发到思考目标问题进而解决问题.但由于学生认知的局限性，抓不住问题的本质，往往不能直接根据已知条件，将要求的问题化归为已解决的本原问题，进而形成问题的解决策略.另外，由于课堂教学时间紧、任务重，教师仅仅关注内容或方法有没有讲清楚或透彻，很少深挖问题的源与流,学生往往不能从问题的本原考虑，形成解题的基本思路，从而造成只要问题条件稍作变化，就不会解的困境.本原思想是相对学生而言的最朴素、最本质的想法[1].

从问题的本原考虑就是以认清问题的本原为基础，探寻解决问题的基本方法与规律，达到善于解题的目标.笔者借助一道高考模拟试题的评讲过程，让学生基于目标解题意识，回归到本原问题考虑，奠定融会贯通的基础，形成良好的解题思维习惯，实现高效解题.

1 学习过程

(2016年5月江苏省南京、盐城数学高考模拟试题第14题)

对于该题笔者所在学校学生做得很不理想，全校共560人参与此题，仅有42人做对.后期笔者在对答对的学生访谈时，发现他们虽然做对了，但过程千奇百怪，而且复杂，带有很多偶然的因素，大多数学生根本没有把握问题的本原.

环节1基于目标， 探寻本原.

师：例1是什么问题？以前有没有遇到过类似的问题？

生1：与2011年浙江省数学高考理科试题第16题(即例2)类似.

例2若实数x，y满足4x2+xy+y2=1，则2x+y的最大值为______．

师：分析很到位，以“形异神似”的高考题作为本原，非常符合模拟试题的特点，那么解决例2有哪些方法？

生1：由已知条件知道x，y的关系，于是，联想利用基本不等式来解决它.

4x2+xy+y2= (2x+y)2-3xy≥

即

得

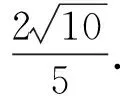
师：非常好！还有其他方法吗？

则

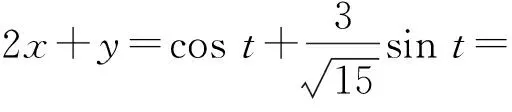
师：太棒了!生2思路清晰、自然，别的同学还有不同想法吗？

生3：对所求式子平方得(2x+y)2=4x2+4xy+y2，因此我联想到了三角函数求值中的齐次式处理方法，即

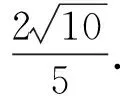
生4：整体思想是解决多元问题的常用策略.令2x+y=t，则y=t-2x,将其代入方程4x2+xy+y2=1,得

6x2-3tx+t2-1=0，

可将其看成是关于x的一元二次方程且该方程有解，从而

Δ=-15t2+24≥0，

于是

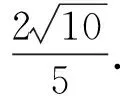
生5：例2的本质是动点P(x,y)在曲线4x2+xy+y2=1上移动.令2x+y=t，则直线y=t-2x与曲线4x2+xy+y2=1有交点，得

Δ=-15t2+24≥0，

从而

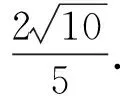
师：让我给大家对比、分析一下.生1是利用不等式法处理的，需要适当变形，更要注意使用基本不等式中等号取得的条件；生2从已知条件结构入手，使用消元法，借助三角换元法，将问题转化为三角函数求最值，思路较为顺畅；生3受到三角函数中齐次式求值的启发，也将问题转化为三角函数求最值，值得学习；生4使用方程法，整体思想应用很恰当，生2、生3和生4的策略都达到了消元的目的；生5采用的是线性规划策略，其本质可看作直线(或曲线)与曲线有交点的问题.

设计意图通过熟悉的高考题作为本原，驱动课堂教学的进行，将本原问题融入到揭示、探究数学本质的活动过程中，实现一题多解，多解归一，形成解决一类本原问题的基本方法.

环节2基于目标，回归本原.

师：同学们，根据例2的研究，我们归纳出多种解决策略，现在能否利用这些方法来解决例1？

生6：目标问题比较繁琐，分子是一次式而分母却是二次式，不知道该怎么做，如果分子、分母次数都是一次或二次，就可以用齐次式处理了.

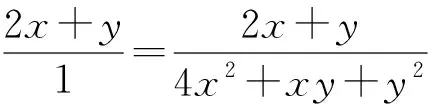
5x2-2xy+2y2=(x-2y)2+2,

从而

师：太棒了！其他同学听明白了吗？

(学生们纷纷点头.)

师：请用生7提供的思路解出答案.

师：当思路不“通畅”时，自然需要调整，向已经解决的本原问题靠拢，正可谓“山穷水尽疑无路，柳暗花明又一村”.

生8：我试图将目标问题转化为关于x(或y)的一元函数，但没能成功.于是，调整了思路，选用生2的方法，也没成功，但得到了

(2x-y)(x+y)=1.

令2x-y=m，x+y=n，则mn=1,且

师：太棒了!从本原高考题出发，提炼方法，运用于新题之中，实现了“解一题，通一类”，这才是真正的数学解题学习.基于目标意识，回归到问题的本原，从而奠定融会贯通的基础，形成良好的解题思维习惯，实现高效解题.

设计意图模考题(文首例1)经过包装，将其本原隐藏起来，进而达到考查学生转化问题和解决问题的能力；从问题的结论深入，发现其中与本原问题的联系，在“形异神似”中实现方法的正向迁移，达到“解一题，通一类，带一串，提一片”的目的.

环节3链接高考，强化本原.

师：江苏省数学高考题中也有此类问题的影子，比如下面两道题，同学们课后可以尝试着用本节课学到的方法解决它.

(2012年江苏省数学高考试题第14题)

例4在锐角△ABC中，若sinA=2sinBsinC，求tanAtanBtanC的最小值.

(2016年江苏省数学高考试题第14题)

设计意图链接高考题，提升学习兴趣，发展学生的思维，实现对知识方法的深层次理解和灵活应用等目的.

2 几点思考

2.1 注重目标意识

数学解题正是在问题的初始状态和目标状态之间进行比较、分析、消除差异，最终找到达到目的的最佳路径的过程.基于目标意识解题，就是首先根据目标任务弄清“要什么”，清楚问题的特点，然后理清“有什么”，选择方法，缩小“有什么”和“要什么”之间的距离，进而尝试怎样缩小．“目标意识”和“正难则反”的解题思想也是中学生应该具备的基本数学素养.解题教学中，教师应多关注、培养学生基于目标的解题意识，当学生遇到复杂问题、由条件到结论的常规解题思路受阻时，就会主动尝试从结论出发，寻求解决问题的突破口，这样有助于培养学生思维的敏捷性和发散性.

2.2 注重问题本原

项武义教授曾说：“必须要对基础数学的本质和基本思想下一番深切的方璞归真.”这正是要让学生养成将复杂问题退到最简单、最原始问题的思维习惯最好的诠释.“本原思想”是指将一个数学问题的要素和基本结构作为思考的始点，是相对学生而言的最朴素、最本质的想法.回归本原问题，驱动解题教学，能够充分发挥教师的主导作用.解题教学应引导学生探寻问题的本原，让学生“跳一跳”就能够到；应抓住问题的本原，弄清问题的源与流，有意地将问题回归为已解决的“本原问题”，自然生成解题思路.

2.3 注重通性通法

章建跃博士认为：“注重通性通法才是好数学教学.”解题需要基于目标，回归本原问题发现一类问题的方法结构，然后进行辨识，找共性，获得一般结论、想法，形成一类问题的通性通法；让学生掌握“一招一式”的通性通法，明确方法的普遍性，具有回归问题本原、联想通性通法的意识，具有一双透过现象看本质的慧眼，才是解题教学追求的长远利益[2].

2.4 注重联想能力

数学家波利亚说：“货源充足和组织良好的知识仓库是一个解题者的重要资本．”数学解题，更多的是在新情况和条件下去寻求未知的东西[3].数学解题思路寻求应该基于已有的认知结构进行思维方法联想.作为教师，要根据学生的实际状况选择恰当的题，选择恰当的讲题方法，最大限度地培养学生解题的能力.笔者认为，至少在还没有找到更好的方法之前，“基于目标，将新问题表征为自己头脑中所熟悉的‘本原问题’，进而联想问题解决的方法”是一个可行的好方法.

总之，解题的首要目的是巩固概念，最终目的是学会思考，过程中要培养良好的解题习惯，发展分析和解决问题的能力.基于目标，依据结论的形式，回归本原问题的解题思维，才能使学生真正学会思考.