一道湖北省预赛试题的多视角解答*

●

(合肥市第一中学,安徽 合肥 230601)

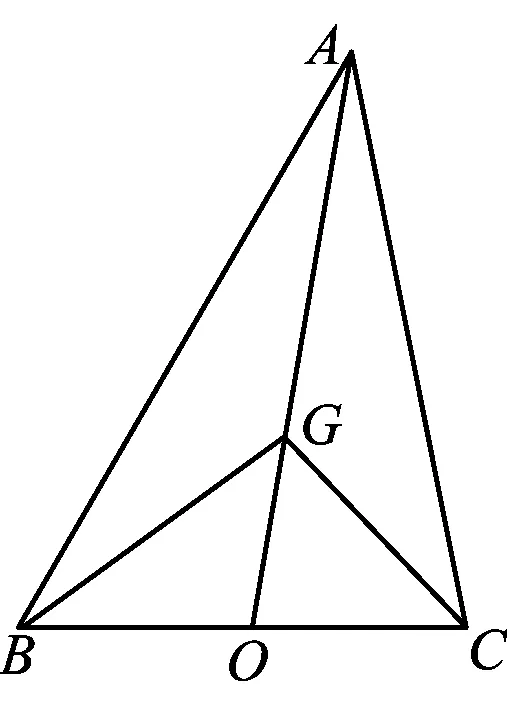
图1

(2018年全国高中数学联赛湖北省预赛试题第5题)

分析本题以解三角形为载体，利用重心性质和位置关系，最终确定三角形另外两边之和的最大值.题目短小精炼，条件也不是很多，但是在解题的过程中还是会遇到一些阻碍.笔者特将自己答题的4个视角7种解法记录下来，以飨读者.

视角1坐标.

由均值不等式,得

评注将几何问题代数化是常见的方法，此视角下将点的坐标用参数表示出来，最后利用均值不等式解之.

视角2几何.

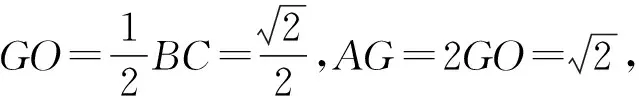
即

于是

解法3在解法2中，若不用中线定理，则在△ABO中，由余弦定理得

同理，在△ACO中，由余弦定理得

两式相加得

x2+y2=10,

因此

解法4设∠AGB=α,∠AGC=β，由S△GBC=S△GBA=S△GAC，得

从而

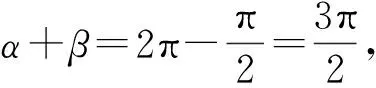
于是

(1)

同理，在△AGC中,

(2)

式(1)+式(2)，得

x2+y2=10，

下同解法3.

评注几何问题几何解，注意到底边及底边上的中线长已知，求两腰长的和的最大值，自然想到中线长公式，如果不知道公式也没关系，利用余弦定理可证之.

视角3向量.

即

于是

又

2xycos∠BAC=x2+y2-BC2=x2+y2-2,

故

x2+y2=10,

下同解法3.

(7)

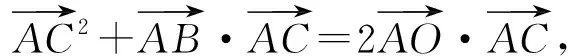
(8)

式(7)+式(8),得

下同解法5.

评注向量是联系几何与代数的纽带，三角形中也经常有一些经典的向量结论，一些常见的结论很多是用向量证出来的，此题用向量求解过程简洁、自然.

视角4猜想.

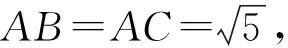
评注猜想，因为没有给出严格的证明，从某种意义上来说不能算一种解题方法，最多是一种“投机”的思路，但不可否认的是在解决一些选择题和填空题时，猜想能带来意想不到的效果.

波利亚说：“掌握数学就意味着善于解题.”本题解题思路明确，学生很容易从这4个视角找到突破口，这就需要我们在日常教学中让学生彻底理清楚常见的解题思路，即“什么时候用，什么条件下用，怎么用”[1].本题的诸多解题视角启示我们:教师要改变传统教育观念，重视教学本质的挖掘，重视对学生数学素养的培养，针对数学解题教学，更应该围绕数学基础知识的合理组织与运用、基本方法的不断深化展开，而不能仅仅是题目类型、解题技巧的归纳和训练.