多种视角 精彩纷呈*——2018年江苏省高三六市联考填空压轴题的多解

●

(侯集高级中学,江苏 徐州 221121)

2018年3月江苏省徐州、淮安、宿迁、南通、扬州、泰州六市高三学生进行了联考.笔者所在学校(江苏省首批四星级高中)高三共有学生905人，其中第14题(填空压轴题)仅有4人做对.经调查，90%的学生看完题目略作尝试就放弃了，可见此题难度较大.该题主要考查函数的最值问题，在知识的交会处命题，构思新颖、设计简洁.笔者给出5种解法，以飨读者.

1 试题回放

2 不同视角下的解法

恒成立，且能取得等号，于是

225x4-72(a+1)x2+16(a-1)2≥0

恒成立，且能取得等号，其判别式

Δ=722(a+1)2-4×225×16(a-1)2=0，

即

3(a+1)=±5(a-1)，

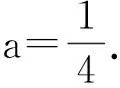
说明将函数的最值问题转化为恒成立问题，通过一步步变形，转化为二次函数恒成立问题，利用判别式进行处理，思维量不大，计算量不小，算出来需要勇气.

解法2(柯西不等式法)

从而

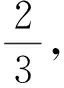
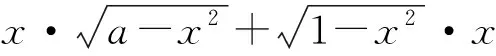
解法3(导数法)

依题意得

说明通过导数研究最值是最保底的方法，在没有使用导数之前都不能说已经尽力了.事实上这道题算到最后发现求导其实并不难算，学生最缺乏的是勇气！

图1

另一方面,

解法5(轨迹视角)由于f(x)为奇函数，现仅考虑当x>0，a>1时的情形：

再令

则

m2+1=an2+a，

即

图2

此时Δ=0，即

化简得

4a2-17a+4=0，

说明将本题的分式函数中的变量相对集中到分母上，再通过换元转化为直线与圆锥曲线的位置关系，利用规划知识求解，不失为一种常规手段，体现了通性通法.

3 解后反思

此题立足函数和不等式的基本概念和性质，涵盖知识面广，难度较大.笔者从不同视角思考，产生了判别式法、不等式法、导数法、几何法、解析法等方法，涉及了函数与方程、数形结合、转化与化归及分类讨论等数学思想.

多视角解题可以对某一问题从不同方位、不同侧面、不同层次进行全面的探讨，拓宽学生的视野，培养学生的发散思维.但一题多解不是终点，教师还应该引导学生对多种方法进行对比分析、适当筛选，从中择优，达到弄通一题而旁通一批，让学生有“会当凌绝顶，一览众山小”的探索勇气，达到举一反三、事半功倍的教学效果.