能用拉格朗日中值定理解决不等式恒成立问题吗
云南师范大学数学学院 孔德宏 龚 珏 (邮编:650092)
不等式的恒成立问题一直是高考数学的热点,大致可以分为两种类型:一是含参不等式恒成立,求参数的取值范围;二是证明不等式成立.
用拉格朗日中值定理来解决不等式的恒成立问题具有高等数学背景,通常情况下解题过程简洁,解题方法新颖.但这样做对吗?如果对,其依据是什么?如果不对,那问题又出在哪里?下面来研究这一问题.
1 含参不等式恒成立,求参数的取值范围
例1 已知函数f(x)=ex+x-1,若对任意x∈(0,+∞)都有f(x)>kx恒成立,求k的取值范围.
解法1 (分类讨论)
令g(x)=f(x)-kx,则g(x)=ex+(1-k)x-1>0对x∈(0,+∞)恒成立.
易知g(0)=0,g′(x)=ex+1-k,且g′(x)是增函数,所以g′(x)>g′(0)=2-k.
(1)当k≤2时,g′(x)>0,所以g(x)在(0,+∞)内是增函数.从而g(x)>g(0)=0,即k≤2满足题意.
(2)当k>2时,令g′(x)=0,即ex=k-1,易得x=ln(k-1)>0.
因为g′(x)是增函数,所以当x∈(0,ln(k-1))时,g′(x)<0,g(x)是减函数.
所以当x∈(0,ln(k-1))时,g(x) 综上,得k≤2. 显然f′(t)在(0,+∞)内单调递增.所以k≤f′(0)=2,故k≤2. 说明 两种解法,答案相同.其中解法2使用了拉格朗日中值定理,避免了分类讨论,从而简化了解题过程.由此似乎可得出:求含参不等式恒成立问题中参数取值范围的问题,用拉格朗日中值定理是一个较好的解题方法. 事实真的是这样吗?我们试着用同样的方法解决例2. 例2 已知函数f(x)=ex-x2-1,若对任意x∈(0,+∞)都有f(x)>kx恒成立,求k的取值范围. 因为当x∈(0,+∞)时,ex-x-1>0,所以当x∈(0,1)时,g′(x)<0,g(x)单调递减;当x∈(1,+∞)时,g′(x)>0,g(x)单调递增.所以k 故k的取值范围为(-∞,e-2). 令g(t)=et-2t,则g′(t)=et-2. 令g′(t)=0,得t=ln2,易知g(t)在(0,ln2)内单调递减,在(ln2,+∞)内单调递增.所以g(t)min=g(ln2)=eln2-2ln2=2-2ln2. 故k<2-2ln2,即k的取值范围为(-∞,2-2ln2). 说明 两种解法,答案不同.经认真检查,可以确认解法1是正确的,从而,这里的解法2肯定就出错了,可究竟错在哪里?特别地,例1中的解法2(拉格朗日中值定理法)为什么算出的答案又是正确的呢? 而例1和例2的解法2却都把问题转化为k 例3 已知函数f(x)=ex+x-1,x∈(0,+∞),求证:f(x)>2x. 证明 (拉格朗日中值定理) 又因为f′(t)=et+1在t∈(0,+∞)内单调递增,所以f′(t)=et+1>2. 例4 已知定义在(0,+∞)内的函数f(x)=xe-x. 结论1 已知含参数k的不等式对x∈D恒成立,求参数k的取值范围的问题(如例1、例2),若能用拉格朗日中值定理,把问题转化为k


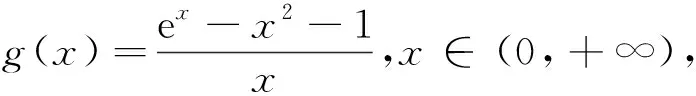


2 错因分析


3 用拉格朗日中值定理证明不等式



4 关于D*⊆D的典型例子

5 结论


