关于正比例函数、一次函数和反比例函数教学的几点思考
上海市岭南中学 刘华为 (邮编:200435)

1 关于四种典型教材不同处理方式的思考
笔者认真研读了人教版、北师大版、华师大版和上教版教材,对比各版本不同的处理方式,真切地感受到编者在进度安排、内容取舍和细节处理等方面的精心雕琢与匠心独运,也对三个函数的教学有了全面的理解和深度的思考.
从进度安排上来看,人教版教材把正比例函数和一次函数的教学安排在八年级《数学》下册(第19章“一次函数”),反比例函数安排在九年级《数学》下册(第26章“反比例函数”)学习,期间还穿插学习了二次函数;北师大版教材把正比例函数和一次函数的教学安排在八年级《数学》上册(第4章“一次函数”),反比例函数安排在九年级《数学》上册(第6章“反比例函数”)学习;华师大版教材则把这三个函数的教学均安排在八年级《数学》下册(第17章“函数及其图象”);上教版教材把正比例函数和反比例函数的教学安排在八年级《数学》下册(第18章“正比例函数和反比例函数”),一次函数则安排在八年级《数学》下册(第20章“一次函数”)学习.单就进度安排而言,笔者更欣赏华师大版教材把三个函数安排在同一章节的处理策略,减少了由于跨时段学习引起的知识遗忘而造成的长时间旧知复习环节,既突出三者之间的关联性,又使教学一气呵成,更有利于知识迁移和新知的有效生成;人教版教材把二次函数的学习放在反比例函数之前,使学生对函数图象有了直线和抛物线两种认识,为画反比例函数图象时需用光滑曲线连接相邻两点埋下了伏笔,降低了难度.特别是从函数解析式的特征来看,沿袭了从整式到分式的学习习惯,尊循了认知规律,注重了学情发展;上教版教材把反比例函数教学穿插在正比例函数和一次函数之间,意在突出正比例函数和反比例函数在认知方式的相似度和性质学习的对比度,虽有一定的创新,但却有违认知规律之嫌,毕竟从正比例函数到一次函数的迁移更自然,两者联系也更紧密,尤其学生在掌握一次函数图象也是一条直线后,更易理解画反比例函数图象时为什么相邻两点之间需用光滑曲线连接(后文将详细阐述);相比较而言,北师大版教材却显得中规中矩,沿袭了传统的进度安排,自然也就缺少了创新味.
从内容取舍来看,单就性质而言,相同的是上述四个版本教材均把函数的单调性和反比例函数所在的象限与k的符号关系作为教学重点,无论是新知生成还是性质应用都作了精心安排,以突出其重要性.不同的是,对于“正比例函数图象与比例系数k的符号关系”和“一次函数图象所经过的象限与k和b的符号关系”,上教版教材均把二者归纳为性质,并作为教学重点以突显其重要地位;人教版教材只把前者作为性质,至于后者则通过一道习题(配套教材99页第12题)引导学生自我归纳整理,重要性自然也就打了折扣;而北师大版教材和华师大版教材对二者均淡化处理,不仅没有作为性质,而且只是通过一道习题(分别见北师大版配套教材第99页第8题和华师大版配套教材习题17.5第1题)对其中一两种情形偶有涉及,学生能否全面掌握要取决于教师对教材的处理能力和学生的感悟与迁移能力,其重要性自然也就更加逊色了.那么学生掌握这两个性质究竟有没有积极意义呢?首先有助于学生对函数单调性的理解与认识.试设想一下:当k>0时学生脑海里浮现一次函数的图象必经过第三、第一象限,并自左至右逐渐上升,那自然就能理解函数值y是随着x的增大而增大了;其次有利于对函数及其图象的全面认识.众所周知,研究图形主要包括形状、大小和位置,对于函数图象当然也不例外,更何况让学生了解k决定一次函数图象的形状(即变化趋势)且b决定图象的位置,还为高中学习直线的斜率与截距奠定了坚实的基础;最后有利于学生能力的发展.在探究图象位置与k和b的符号关系时,对培养学生观察能力、分析能力和归纳能力都大有裨益,特别是关于“若直线y=kx+b不经过第一象限试确定k与b的取值范围”这类逆向思考的问题,无疑就是训练学生思维严谨性的绝好素材.更何况增加这两个性质的学习并未过重增加学生的负担,反而为解决类似问题提供了知识基础、思路引领和方法指导,实乃有利无害也!
从细节处理来看,人教版教材关于性质“k>0时正比例函数图象经过第三、第一象限”的表述就比上教版教材的“k>0时正比例函数图象经过第一、第三象限”的表述更为精妙与科学,虽然有违数字从小到大的表达习惯,但却与“图象从左至右逐渐上升”及“y随着x的增大而增大”性质中关于x的变化趋势的表述高度吻合,便于学生理解与掌握性质;北师大版教材非常注重知识生成过程的精心设计,每条性质的形成都要经过“做一做”“想一想”和“议一议”等环节,让学生在动手操作、独立思考、相互讨论和归纳完善后才逐步掌握.换言之,学生是性质的建构者,全程参与了知识的生成过程,自然对性质的理解与应用也就更加得心应手;华师大版教材在注重知识生成过程的同时还更加注重生本互动环节的精心设计,每条性质都没有直接显现在教材中,而需要填写关键词甚至关键句.这就有效避免了只重结果的走马观花式教材阅读方式,促成学生要想得到性质就必需完成教材设计的探究过程.特别是,学生独立思考总结的性质未必科学与完善,但经历与教师提供的标准答案对比反思后,必然能强化思维的严谨性和语言的规范性,从而提升归纳整理能力,可谓一举多得也.
基于以上分析,笔者依托所执教的上教版教材涵盖内容最为全面的特征,优化整合其他版本教材的科学处理方式,围绕“图象所经过象限与k和b的符号关系——单调性——平行性(两个一次函数图象的位置关系)——直线的倾斜度(或反比例函数图象与两坐标轴的趋近度)与k的绝对值的大小关系”等性质,大胆设计出“正比例函数——一次函数——反比例函数”的一体化教学流程,采用“做一做——想一想——议一议”的互动式学习模式,以促进学生在参与性质建构的过程中认识性质理解性质用好性质,也取得了不错的效果,但究竟是否科学还有待专家进一步指正.不过,身为一线教师当然更加期待能有一套能集众家之长的完善教材为己所用,以求在教学实施中水平自然上升到一定的高度,从而大大提高课堂效率,造福学生,毕竟个人对教材的研究水平和处理能力皆十分有限.
2 关于课堂教学热点的思考
2.1 由实际问题引入真的那么重要么?
据笔者调研,皆由实际问题引入三个函数的概念是所有教材(不仅局限于本文所涉及的四种教材)的共同处理方式,也是广大同仁的统一授课模式,变化仅局限于所选取的背景材料不同而已.不过2017年5月8日在黄山市举行的以“创新”为主题的第三届全国名师展示课活动中,笔者所执教的“一次函数(第一课时)”却从平移入手,借写出由正比例函数y=kx的图象向上和向下平移后所对应的函数解析式引入一次函数的概念(详细过程请参考文),以突出了两个函数间的本质联系,促成由正比例函数到一次函数各性质的纵向迁移,体现了由旧知到新知的递进式发展模式(而教材均由实际问题引入却是一种独立的平行关系,未能很好地反映两个函数之间的本质联系),创新味浓厚,也得到了观摩老师和与会专家裴光亚教授的充分肯定(见文).
但笔者在参加区职称评审时,同样的设计却受到某位评委的“质疑”:如此设计难道不会给学生造成一次函数是由正比例函数图象平移而来的误解吗?该专家指出一次函数就是来源于实际生活,课堂教学务必要尊重教材的处理方式,切不可随意设计.且不说一次函数是否一定由实际问题衍生而来,单就学生的认知方式而言可谓是丰富多彩千变万化,完全没有必要被“数学来源于生活又服务于生活”的理念套死,更何况形式是为内容服务的,无论一次函数是来源于生活提炼也好,还是来源于旧知迁移也罢,只要教学设计能引导学生主动参与建构,凸显知识间的本质联系,便于理解、掌握与运用新知,推动能力的发展,就不失为一种成功的创新设计,完全不必刻意追究其源于何处成于何方.否则,就有固步自封甚至舍本逐末之嫌了,毕竟教材是用来用的而不是用来套的.
2.2 仅观察图象是否为学生获取性质的完善方式?
毫无疑问,先描点画出函数图象,再通过观察图象得出函数相关性质是初中生学习函数的主要认知方式,意在借助形的直观性强化学生对函数性质的认识与理解,以突出数形结合思想,特别是用形研究数的优越性.但笔者在教学实施中发现一个奇怪的现象:总有学生在运用性质处理问题时犯了“反用”的低级错误(如对于正比例函数y=kx而言,常把k<0与k>0的结果相混淆),虽然经过大量习题反复操练后似乎达到熟能生“巧”了,但随着时间的推移这类错误往往又会在部分学生中死灰复燃.
那么这类错误形成的根源究竟何在?解决问题的突破口又在哪里?笔者经过大量的调研后发现,其根本原因在于学生对两个函数性质的学习只关注了记忆没有注重理解,这当然与教师对图象与性质的教学方式密不可分.首先,通过观察图象得出性质就是一种典型的记忆性学习,只不过突出了直观性,便于加深印象而已;其次,教师的口诀式教学也对记忆性教学有推波助澜之效.如口诀“撇大捺小吃定k、上正下负锁死b;增大增大线为撇、增大减小线为捺(意思是指:直线为撇k为正,直线为捺k为负;直线与y轴交点在x轴上方时b>0,直线与y轴交点在x轴下方时b<0;函数值y随着自变量x的增大而增大直线为撇,函数值y随着自变量x的增大而减小直线为捺)”虽然言简意赅生动形象,但只加深记忆,根本无助于学生对性质的理解;最后,大量重复操练的配套习题也只是发挥培养熟练工的“特”效,本质上还在加强记忆,无法真正期待由量变引起质变.总之,这些强化记忆性的教学策略,无论怎么挖掘抑或创新,都不能加深学生对性质的理解,一旦出现记忆紊乱,即使面对经过一三象限的一次函数图象学生也想不起k>0了.
那么如何才能加深学生对性质的理解呢?笔者的体会是对函数性质教学切忌过于依赖形的直观而忽视对数的分析,务必要加强“以式析性”(即根据解析式剖析性质的理论依据)研讨,引导学生不仅经历“由形到数”的观察,还体会“由数到形”的演绎,才能成“数形结合”两全之美也(“数无形少直观,形无数难入微”).具体地说,如对于正比例函数y=kx而言,由图象得出“当k>0时图象经过第三、第一象限和y随着x的增大而增大”后,再从数的角度深入分析,引导学生理解:正是由于k>0,所以y与x同正同负,对应点的横纵坐标同号,因此图象必然经过三一象限;同样正是由于k>0,当x1 众所周知,用描点法画反比例函数图象是教学的一大难点,基于正比例函数与反比例函数的相关性,课堂教学往往通过回顾用描点法画正比例函数图象的基本步骤,引导学生仿画反比例函数图象.遗憾的是,学生画出的反比例函数图象往往错误百出,如光滑曲线变成折线、两支变一支、图象与坐标轴相交和图象在无限趋近两坐标轴时突然转向等.而造成上述错误的“罪魁祸首”正是教师所设计的由画正比例函数向画反比例函数图象迁移情境,由于两个图象差异较大(形状由直到曲、数量由一条到两支、与坐标轴交点从有到无等),根本无法直接迁移,学生依葫芦画瓢,出错自然也就在所难免了. 对照问题3,可放手让学生自己分析归纳,再次体验“由式想形”的过程,逐步归纳出:当x逐渐减小时y的值逐渐增大,且越来越接近于0但始终小于0,所以图象越来越接近于x轴(但始终在x轴的下方)且向左无限延伸;当x值越来越接近于0(始终小于0)时,y的值越来越小,所以图象越来越接近于y轴(但始终在y轴的左侧)且向下无限延伸. 描点法画反比例函数图象时,学生常常把相邻两点用线段连接(即把图象画成折线).针对这一现象一般认为是学生缺少由直线到曲线的必要迁移经验所致,即在画反比例函数图象之前,学生只画了直线型的一次函数图象,因而不可能想到要用光滑的曲线连接.不过笔者对此却有不同的思考,认为缺乏对一次函数(含正比例函数)图象的深度解读才是学生犯错的根本原因之所在.如果在学习一次函数时不只是让学生掌握一次函数y=kx+b(k≠0)的图象是一条直线,而且还了解常函数y=b的图象是一条平行于x轴的直线、x=a表示的是一条垂直于x轴的直线;反之,平面直角坐标系内任一条不平行于坐标轴的直线对应的解析式只能是一次函数y=kx+b(k≠0),平行于x轴的直线的解析式只能为常函数y=b,垂直于x轴的直线只能表示为直线x=a,且线段和射线的表达式也只能是这三者之一,不同的是变量的取值范围不再是一切实数,而是其一部分.有此铺垫,学生在画反比例函数图象时,至少相邻两点不可能再用线段(或折线)连接了(也正因为如此,上教版教材把一次函数的教学安排在反比例函数学习之后就略显不妥).至于为什么一定要用光滑曲线,不妨作如下解读:由横坐标x的从小到大(或从大到小)依次取值排除了左右起伏的波浪线(其实,这种图形也不可能作为函数图象,否则一个x值对应多个y值,与函数的定义相矛盾),而根据函数值y随着x的增大而减小(或增大)又可排除上下起伏的波浪线,故而只能用含一定变化趋势的光滑曲线连接了. 有同仁担心:常规的处理策略(即教材的处理方式)是引导学生先用描点法画出反比例函数的图象,再观察图象得性质,而“由式想形”的处理策略却是先依据解析式得出性质再画图象,是否违背了学生的认知规律?其实这就是“由形到数”和“由数到形”的问题,而这是“数形结合”的两个方面,都是学生的认知方式,并没有违背认知规律之嫌.更何况著名数学家华罗庚教授强调“数无形少直观”且“形无数难入微”,只有把两者有机地融合才是完善的认知方式.但问题在于“先形后数”时,由于学生缺乏必要的作图经验和认知基础,无法独立画出图象(除非事先知道形状),只能依赖教师逐步纠错“引导”,强加味浓厚,可信度却淡了不少.大有明知不可为却偏为之的悲壮,意在让学生体验作图的操作过程,获得的却是错误百出的尴尬.而且由于受前摄抑制的影响,这些先入为主的错误往往会对学生后续学习造成不少负迁移.而“先数后形”却不同,学生不仅易于接受由解析式剖析性质的切入点,还能获得描点法正确作图的成就感,最后体验由图形观察性质的直观感受,岂不两全齐美?特别是“由式想形”的处理策略有利于培养学生“先理性分析再动手操作”的良好思维习惯和处事习惯,对其后续发展更有深远的意义.更何况,先画图再纠错是强塞,而“由式想形”则基于理解,熟优熟劣一目了然. 当然,关于课堂教学的思考可谓“仁者见仁智者见智”,也很难有个统一标准或完美的答案.但不管怎样,加强对不同版本教材和相关论文的研究,集百家教研成果之精华,并结合教学实践大胆探索与反思,在基于知识理解和能力之上积极寻求突出重点的设计和突破难点的对策,不断提高课堂效率,也许是每一位执教者走向成熟并不断提升的有效途径.2.3 画反比例函数图象的切入点究竟在哪里?
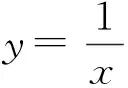
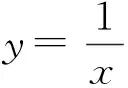
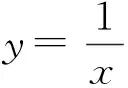
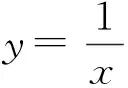
2.4 学生错把反比例函数图象画出折线的根源在何处?
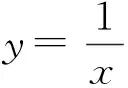
2.5 “由式想形”画图象是否有违学生的认知规律?

