2018年高考数学阅卷有感——兼谈文科生的现状及教学启示

安徽省砀山中学 盖传敏 (邮编：235300)

笔者有幸参加了2018年安徽省高考数学网上阅卷工作，面对学生的数学试卷及其出现的问题，感触颇多，下面笔者根据2018年全国卷(I)文科数学第19题的阅卷情况，谈谈文科生的现状及教学启示.

1 试题再现

(2018年全国卷I文科数学第20题)设抛物线C:y2=2x，点A(2,0),B(-2,0)，过点A的直线l与C交于M、N两点.

(1)当l与x轴垂直时，求直线BM的方程；

(2)证明：∠ABM=∠ABN.

2 试题综述

此题是一道以抛物线为背景的解析几何问题，知识上主要考查直线方程、抛物线性质、直线与抛物线的位置关系等，思想上主要考查转化化归与数形结合等思想，常见的背景、简单的问题、基本的方法，笔者认为绝大部分考生拿到该考题都会倍感“亲切”，获得不错的分数，但获得阅卷统计结果后笔者大呼意外，此题全省平均分为5.12(含0分) ，6.23( 不含0分) ，如此结果，反映了当今文科生数学素养的严重缺失，同时也反映了平时教学中教师对解析几何问题只重视“解”与“析”，而轻视解题过程的具体运算与算理的揭示，忽视学生核心素养提升的结果，这不得不令人反思.

3 考生解法赏析

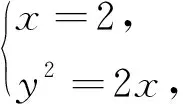
(2)思路1 利用斜率求证

解法1 设直线点斜式方程求解

当直线l斜率不存在时，由抛物线的对称性易知∠ABM=∠ABN；

则直线BM、BN的倾斜角互补，所以∠ABM=∠ABN；综上所述∠ABM=∠ABN.

解法2 设直线方程x=ny+m求解

思路2 利用角平分线性质求解

解法3 由题意可知，直线l斜率不为0，可设直线l的方程为x=ny+2，

则y1+y2=2n,y1·y2=-4，由直线的两点式方程可得，lBM:y1x-(x1+2)y+2y1=0，lBN:y2x-(x2+2)y+2y2=0，记点A(2,0)到直线BM、BN的距离分别为d1、d2，则

思路3 利用几何性质求解

解法4 由题意可知，直线l的斜率不为0，设直线l的方程为x=ny+2，不妨设M(x1,y1),N(x2,y2)(y1>0,y2<0)，

4 失分原因剖析

4.1 书写不规范导致失分

有些考生字迹不清，书写不工整，版面布局不合理，导致阅卷教师不好辨认，从而导致考生得分点被遗漏，导致失分.

4.2 解题片面不完整导致失分

许多文科考生由于基础薄弱，基本功不扎实，卷面上出现大量的“会而不对，对而不全”的情况，如对于第(1)问，好多同学只求出了一条直线方程，忽略了另外一条直线；对于第(2)问，部分同学在设直线方程点斜式时，忽略了对斜率不存在时的讨论.

4.3 化归意识差，转化能力弱导致失分

对于问题(2)求证∠ABM=∠ABN可转化为直线的倾斜角互补，即斜率(存在)之和为0，可转化点到直线的距离相等，也可转化为平面几何问题，可谓思路开阔，但部分同学不能将问题合理转化，出现了不少0分试卷.

4.4 运算不准确导致失分

对于问题(2)的解法1和解法3，考生在代换、求值、化简等解题过程中出错的情况非常严重，考生即使在解题思路和选用公式都正确的情况下，仍然无法得到正确的答案，有些考生的解题过程戛然而止，这些都是计算能力弱造成的.

5 教学启示

5.1 培养规范答题的习惯

今年高考阅卷对解题规范的要求较高，考生答题的语言叙述必须规范，语言叙述应正确、完整、详略得当，言必有据.教学中，教师应帮助学生明确得分点，哪些可以省略，哪些必不可少，要适时地就典型试题分析评分细则，明确主要步骤，教师要注重板书示范，并在平时练习时，应要求学生按得分点、按步骤书写.

5.2 回归本质，夯实基础

在阅卷中发现，部分文科生的基础知识不扎实，公式记忆不清晰，计算丢三落四，在教学中，我们必须踏实做好数学教学，夯实基础，以不变应万变，只有这样才能在高考中获得成果.

5.3 善于反思，勤于总结

在阅卷中发现，部分文科生思维混乱，不知所出.对于数学能力的提高不仅在于解题的数量，更在于解题的质量，通过反思总结，明确解题思路、数学方法等，通过比较，明确问题的一般思维出发点和问题的不同切入点，最终达到从“做快题”到“做好题”，真正做到举一反三，提高解决新问题的能力.

5.4 注意试题引申和变式练习

笔者发现，该试题与2015年福建卷文科19题背景相同，解法相似，在平时教学中，要认真研究高考真题及大型模拟考试试题，分析试题时不能只就题论题，还应对试题进行适度探究引申，从而提高学生的数学素养.