找寻那最初的“模样”——绝对值函数最值问题的探讨

浙江省上虞中学 李益锋 (邮编：312300)

摘 要 含绝对值的函数在中学数学中是一种较常见的函数,其最值问题在习题和高考中也是屡见不鲜.然而学生遇到这类问题时,往往无从下手,仔细研究后并不是无章可循.笔者对一类含绝对值函数最大值中的最小值从绝对值几何意义角度进行了研究,得出了一个简单、实用的结论,值得推广,以慰读者.

关键词 数形结合;绝对值函数;最值互嵌

含绝对值的函数通常是指有自变量或关于自变量的代数式包含在绝对值符号之内的一类函数,简称绝对值函数. 纵观近几年的高考试卷，有关含绝对值函数的问题呈现出综合性强、立意新颖、难度大等特点.如果绝对值函数再加上求最值，就使题目难度更加大了，让人感到无从下手.其实，这类含有绝对值最值问题，也并非没有规律可循.我们只要找准做题的切入点，就能把绝对值这层保护膜打开，找到题目最初的模样，顺利地找到思路并解决问题.下面就2016年浙江学考第18题的讲解，来探求这一类绝对值函数最值问题简捷解法.

1 考题呈现

C.(-∞,1〗 D.(-∞,2]

这是2016年4月浙江学考第18题，下面通过三个不同的视角来剖析此题.

视角一 转化为求函数的最值

此题本质为最值互嵌问题，所以可转化为求函数最值.因为存在x0∈2〗，使得f(x0)≥m成立，所以可将此题转化为求M(a,b)=f(x)max≥m,在∀a>0,b∈R成立，进而转化为求M(a,b)min≥m.

视角二 利用绝对值三角不等式

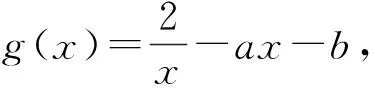
因为f(x)max=max{f(1)，f(2)}=M(a,b)≥m恒成立，

视角三 利用数形结合

图1

2 解法拓展

对此类含绝对值函数最大值中的最小值问题，我们可从绝对值几何意义角度进行研究,把视角三的解法推广成一般情况，可得到如下定理：

定理 设f(x)在闭区间[m,n]上连续，则

这个式子的含义即在数轴上的点f(x)∈[f(x)min,f(x)max]与b之间的距离的最大值的最小值是在当b落在区间[f(x)min,f(x)max]中点时取得的，且此时这个最大值的最小值等于区间长度的一半.

特别地当f(m)=f(n)时，我们还可以得到如下的推论：

3 解法应用

利用以上定理与推论，我们就可以快速地求解以下题目：

例3 设函数f(x)=|x2-ax-b|,x∈[0,1],其中a、b∈R.记f(x)的最大值为M(a,b),则M(a,b)的最小值为______.

思路分析1 构造“平口单峰函数y=x2-x.

思路分析2 设g(x)=x2，h(x)=ax+b，则f(x)=|g(x)-h(x)|,再利用实数之差的绝对值的几何意义求解.

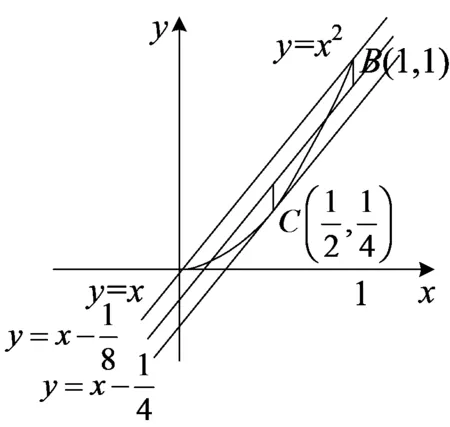
图2

4 解法延伸

例4 设f(x)=4x+1+a·2x+b,(a、b∈

通过上面的几个问题，我们不难发现，通过实数之差的绝对值的几何意义解题，使一些比较复杂的绝对值问题得到巧妙解决，避免了烦琐的分类讨论.这正体现了一个重要的数学思想——数形结合思想，用“形”的直观启迪“数”的计算．我们抓住数形转化的策略，不仅沟通了知识的联系，而且也能激发学生学习的兴趣，从而使学生对数学思想方法有较深刻的理解和掌握.