例谈含参数的绝对值不等式问题及其解法
福建师范大学数学与信息学院 王沛钰 (邮编:350117)
自2017年起,高考数学全国卷的选做题由三选一改为二选一,去掉了选修4-1的几何证明选讲,保留了选修4-4的坐标系与参数方程和选修4-5的不等式选讲.对于不等式选讲的这道选做题,通常设置两问, 每小问5分,总计10分,并且文理同题.纵观近几年高考全国卷不等式选讲的题目,不难发现出题模式以绝对值不等式问题为主.如下表1所示,对2013年―2017年高考全国卷不等式选讲的题目类型统计,可以看出全国I卷近5年有4年考了绝对值不等式问题,全国II卷近5年有3年考了绝对值不等式问题,全国Ⅲ卷自启用连续2年考了绝对值不等式问题.如果对这些绝对值问题进行分析,还可以得到:第(I)问主要考查绝对值不等式的解、画绝对值函数的图象等,此问比较容易;第(II)问多涉及含参数的绝对值不等式问题,题 型灵活,且常考查化归与转化、分类讨论、数形结合等数学思想.通过分析含参数的绝对值不等式问题,总结出了三种常考题型:求参数的值或范围、不等式证明以及绝对值不等式的应用,并结合例子给出了三种常考题型的一般解法,希望对广大的高中师生有所帮助.

表1 2013年―2017年高考全国卷不等式选讲的题目类型统计(全国Ⅲ卷于2016年启用)
1 求参数的值或范围
1.1 已知不等式的解集


例2 已知函数f(x)=|x-a|(其中a>1),若关于x的不等式|f(2x+a)-2f(x)|≤2的解集为x|1≤x≤2,求a的值.
解析 设h(x)=f2x+a-2f(x),则
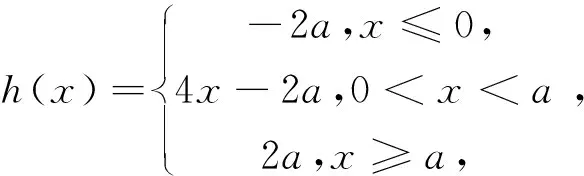

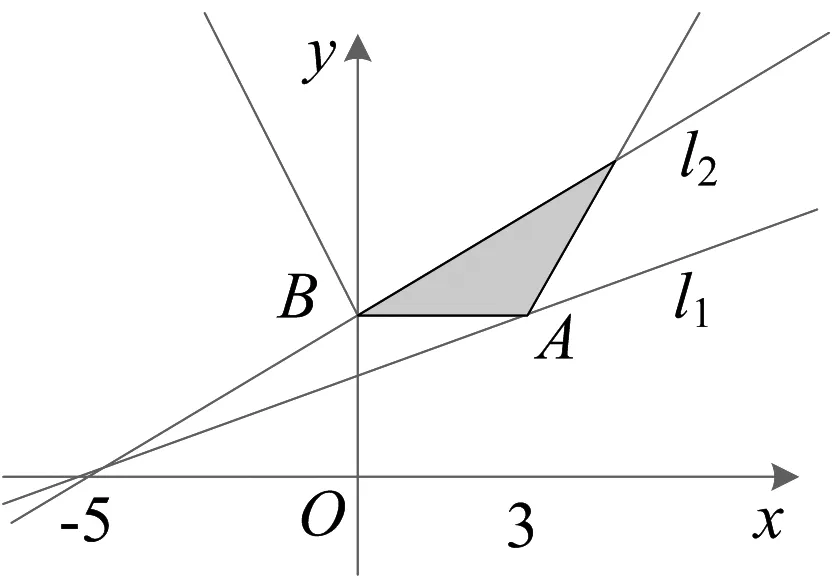
点评 已知含参数的绝对值不等式的解集,如果不等式中只有一个绝对值,我们通常利用|f(x)|>g(x)⟺f(x)<-g(x)或f(x)>g(x),|f(x)| 先求出该不等式的解集,再根据题设列方程(组)或不等式(组)求出参数的值或范围;如果不等式中含有两个绝对值,我们可以考虑分段去掉绝对值来求解集,其中可能会涉及分类讨论,操作起来会稍微复杂一点,需要确保分类讨论的情况不重复、不遗漏. 例3 (2017年高考数学全国卷I·文理23)已知函数f(x)=-x2+ax+4,g(x)=x+1+x-1. (I)当a=1时,求不等式f(x)≥g(x)的解集; (II)若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围. 解析 (I)略. (II)方法一 化归转化思想 方法二 数形结合思想 由于不等式f(x)≥g(x)的解集包含[-1,1],等价于f(x)≥g(x)在[-1,1]内恒成立.又因x∈[-1,1]时,g(x)=2,故可得f(x)≥2⟺-x2+ax+4≥2⟺x2-2≤ax在[-1,1]内恒成立.作出y=x2-2在[-1,1]上的图象,如图1所示,函数y=ax必须落在l1、l2之间,此时kl1=-1、kl2=1.因此a的取值范围为[-1,1]. 图1 例4 已知关于x的不等式|x-a|+|x+a| 解析 因为|x-a|+|x+a|≥|x-a-x-a|=|2a|,且不等式|x-a|+|x+a| 点评 已知恒成立或存在性条件,求参数的值或范围,可以利用化归与转化思想分离参数变成最值问题考虑,也可利用分类讨论思想去绝对值符号直接计算,还可利用数形结合思想画出图象直观观察. 比如,利用化归转化思想分离参数后,若a>f(x)在x∈D恒成立,则a>f(x)max;若a 例5 (2015高考高考卷I·文理24)已知函数f(x)=x+1-2|x-a|,a>0. (I)当a=1时,求不等式f(x)>1的解集; (II)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围. 解析 (I)略. (II)由题设可得f(x)=x+1-2|x-a| 所以a的取值范围为(2,+∞). 例6 已知函数f(x)=x+x-3的图象与直线y=ax+5a(a>0)的图象可以围成一个三角形,求a的取值范围. 解析 图2 点评 已知两个函数图象围成的区域大小或形状求参数的值或范围,关键先要确定围成的区域,再用区域大小或区域形状联系参数,得到满足题意的式子,解出参数的值或范围.如例5中关键是确定三角形区域,进而求出三角形三个顶点的坐标, 其中两点显然是函数f(x)的图象与x轴的交点, 方法一用零点分区间结合图象求交点坐标;方法二是用方程思想求出函数f(x)的图象与x轴的两个交点坐标, 用绝对值三角不等式求出函数最大值继而求出另一点的坐标,等三角形三个顶点坐标求出后,联系面积求参数的范围就变成水到渠成的事情了. 例7 (2015高考数学全国卷II·文理24)设a、b、c、d均为正数,且a+b=c+d.证明: 解析 (I)略. (II)① 若|a-b|<|c-d|,则(a-b)2<(c-d)2,即(a+b)2-4ab<(c+d)2-4cd. 于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.因此|a-b|<|c-d|. 例8 已知函数f(x)=x-2,若a>2,求证:∀x∈R,fax+af(x)>2恒成立. 证明 因为f(x)=x-2,所以f(ax)+af(x)=|ax-2|+a|x-2|=|ax-2|+|2a-ax|≥|ax-2+2a-ax|=|2a-2|,当且仅当(ax-2)(2a-ax)≥0时,等号成立.又因a>2,所以2a-2>2,即fax+af(x)>2,因此,∀x∈R,fax+af(x)>2恒成立. 点评 不等式的证明方法有很多,如比较法、综合法、分析法、反证法、放缩法等,证明时需灵活选择,才能收到事半功倍的效果.绝对值不等式的证明还需联系不等式的性质和绝对值三角不等式(|a+b|≤a+b、a-b≤a±b≤a+b),但要注意取等条件是否满足. 解析 因为f(x)=|x+a|+|x-b|≥(x+a)-(x-b)=|a+b|, 又因a、b∈R+,所以 例10 已知函数f(x)=2x-1,若实数a,b满足a+b=2,求fa2+fb2的最小值. 解析 由f(x)=2x-1,可得fa2+fb2=|2a2-1|+|2b2-1|≥|2(a2+b2)-2|,因a+b=2,利用柯西不等式可得2a2+b2=12+12a2+b2≥(a+b)2=4,当且仅当a=b=1时等号成立,从而2a2+b2-2≥2,即fa2+fb2≥2,故fa2+fb2的最小值为2.1.2 已知恒成立或存在性条件





1.3 已知两个函数图象围成的区域大小或形状
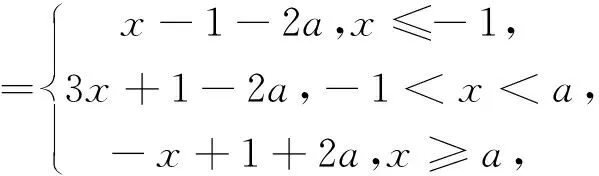

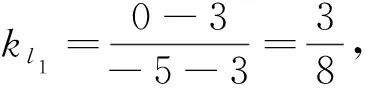
2 不等式证明






3 绝对值不等式的应用:求函数的最值