错在哪里

1 江苏省海州高级中学

佟成军 (邮编：222062)

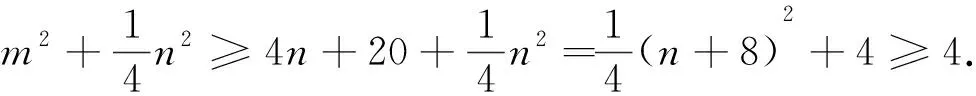
解答错了！错在哪里？

本题是本校编的一道高三练习题，学生给出的基本是这种做法，几乎没人做对．实际上当n=-8时，m2≥4n+20=-12中的等号取不到，所以以上解法是错误的．

正解1 由题设知，x2+mx+n+5=0有实根，所以△=m2-4(n+5)≥0，即有m2≥4n+20．

图1

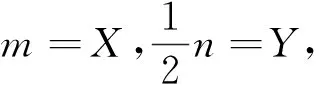
“那里每一样东西都能说出长长的故事来。实习的时候，我最开心的就是去看展，听老师们说故事！”一次，在协助老师撤展时，老师随手指着金丝楠木的展台告诉她，这是由著名文物专家王世襄先生监制的。这种惊喜，在故宫博物院里不胜枚举。也正是在这众多的瑰宝之中，在卧虎藏龙的研究学者之间，宴姝确定了今后的方向——钻研历史，为今后能真正进入故宫博物院工作打好基础。

2 新疆生产建设兵团第二中学

张国治 马士驿 纪 娜 (邮编：830002)

题目 (2017年全国高中数学联赛新疆维吾尔自治区预赛高一试题第8题)

已知数列an首项为2,且满足6Sn=3an+1+4n-1.则Sn的最大值为______.

解析 (标准解答：详见中国数学会普及工作委员会及数学奥林匹克委员会.2018高中数学联赛备考手册(预赛试题集锦).上海：华东师范大学出版社，2018.)

①

解答错了!错在哪里？

错误剖析 事实上,当n=1时,12=6S1=3a2+4-1,得到a2=3,而在上述解答中求出数列an通项an=3n-4n-1中,a2=32-42-1=5≠3,显然上述解答有误.

分析 事实上,此题考查Sn与an的关系,常见的策略是“减元”，即化为只含Sn或an的式子.然后利用等式的基本性质求解.而求解Sn的最值问题,常见的有两个策略：一是从通项an入手,二是直接求出Sn后分析求解.

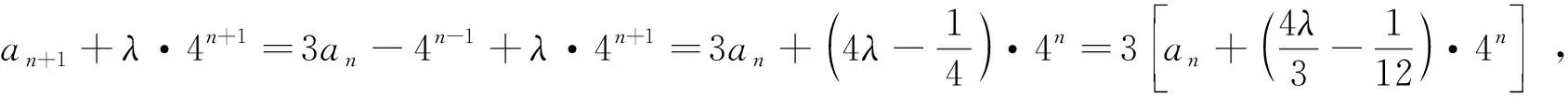
总之,从函数观点看,数列an的本质是定义在正整数集N*上的一个函数,而定义域则为函数的“灵魂”,处理数列问题时刻谨记其本质是函数,若将数列通项公式比作“躯体”,则“定义域”实为数列的“灵魂”.学习数列当务之急是对数列“定义域”深刻理解和把握,否则会陷入“定义域”的误区还自以为是.事实上，通过正本清源发现本质的错误在于命题者忽视了数列的定义域这一隐含条件.