四个有趣的不等式问题的简证

天津水运高级技工学校 黄兆麟 (邮编：300456)

安振平老师在文中提出了三十个有趣的不等式问题,本文对其中的第15号、23号、26号及27号题分别给出简证,供读者参考.

15号题 设a、b、c是实数,求证

≥2(ab+bc+ca)

①

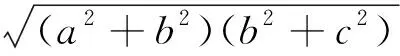
那么①式左边≥(b2+ca)+(c2+ab)+(a2+ca)≥2(ab+bc+ca)=①式右边.

即不等式①成立.以上证明用到了熟知的不等式a2+b2+c2≥ab+bc+ca.

以上根号下局部放缩的技巧还可用到文第23号题的证明之中.

23号题 已知a>0,b>0,c>0且a+b+c=3,n≥2,n∈N,求证

②

本文利用权方和不等式给出一个有趣的证明,供参考.

证 为了能利用权方和不等式求解,特将原不等式②恒等变形为含下界的如下不等式③:

③

从而我们可得

又注意到有幂平均不等式

即不等式③成立,从而不等式②成立.

26号题 设△ABC的三边分别为a、b、c,求证

④

由于不等式④是完全对称不等式,不失一般性,可设a≥b≥c，那么此时易知有

且有2a-b-c≥0,2c-a-b≤0，又设不等式①的左边为M，那么

即不等式④成立,从而原不等式成立.

以上方法亦可解轮换对称不等式问题,即文中的第27号题.

27号题 设△ABC的三边长为a、b、c,则有

a2b(b-c)(a+b-c)+b2c(c-a)(b+c-a)+c2a(a-b)(c+a-b)≥0

⑤

证 由于不等式⑤是轮换对称不等式,不失一般性,可设a最大,那么

当a≥b≥c时,有a+b-c≥c+a-b≥b+c-a，设⑤式左边为M，则

M≥a2b(b-c)(b+c-a)+b2c(c-a)(b+c-a)+c2a(a-b)(b+c-a)

=(b+c-a)[a2b2+b2c2+c2a2-abc(a+b+c)]

欲证M≥0，只需证明a2b2+b2c2+c2a2≥abc(a+b+c)

⑥

⑦

由二元均值定理,容易得出

以上三式相加整理立得不等式⑦成立,从而M≥0成立.

即此时不等式⑤成立.

当a≥c≥b时,有c+a-b≥a+b-c≥b+c-a，设①式左边为M，则

M≥a2b(b-c)(c+a-b)+b2c(c-a)(c+a-b)+c2a(a-b)(c+a-b)

=(c+a-b)[a2b2+b2c2+c2a2-abc(a+b+c)]≥0，

从而M≥0成立,即此时不等式⑤也成立.

综上,知不等式⑤成立.