对一道竞赛试题的探究
2018-08-23 06:11安徽省枞阳县宏实中学江保兵邮编246700
中学数学教学 2018年4期
安徽省枞阳县宏实中学 江保兵 (邮编:246700)

这是2018年全国高中数学联赛湖北省预赛第11题,这是一道条件最值问题,题面简洁,结构工整,但所涉及的数学知识和蕴含的数学思想方法非常丰富,值得深入探究.首先考虑利用柯西不等式化去根号,从而得到最值.
1 柯西不等式
解 由柯西不等式,
考虑到a+b=1,结合柯西不等式等号成立的条件,有


144b4-288b3+263b2+50b-25=0,
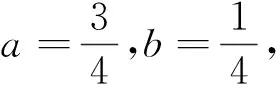

整理得到:


2 函数的观点


解f′(x)=
令f′(x)=0,得到
144x4-288x3+263x2+50x-25=0,
144x4-288x3+263x2+50x-25=(4x-1)(36x3-63x2+50x-25)=0,
h(x)=36x3-63x2+50x-25,h′(x)=108x2-126x+50>0,h(x)>h(0)>0,
3 切线的方法
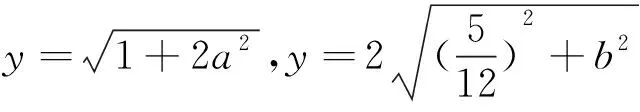
由下凸函数的性质知:k(x)≥k′(x0)(x-x0)+k(x0)=k′(x0)x+k(x0)-x0k′(x0),


144b4-288b3+263b2+50b-25=(4b-1)(36b3-63b2+50b-25)=0,

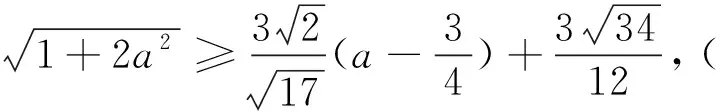

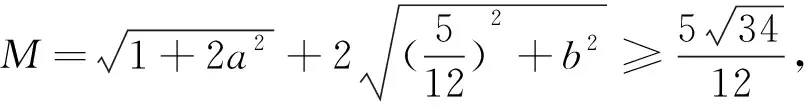
怎么求函数的最大值呢?结合下凸函数的图象,考虑利用闭区间上下凸函数的两个端点所在的直线方程来求凸函数的最大值.
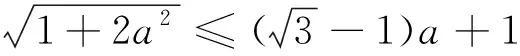


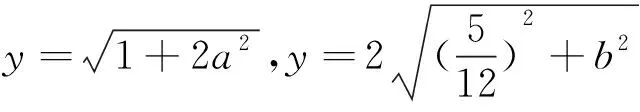
猜你喜欢
语数外学习·高中版中旬(2020年2期)2020-09-10
中学生数理化·七年级数学人教版(2020年3期)2020-08-10
河北理科教学研究(2020年1期)2020-07-24
高中生学习·高三版(2017年6期)2017-06-12
中学生数理化·高二版(2016年5期)2016-05-14
中学生数理化·八年级数学人教版(2016年1期)2016-03-16
安徽农学通报(2015年10期)2015-06-15
中学生数理化·七年级数学人教版(2014年1期)2014-06-20
安徽农学通报(2014年7期)2014-04-29
知识力量·教育理论与教学研究(2013年11期)2013-11-11

