直觉权与直觉模糊子群之间的关系
付云鹏,王利香,袁学海
(1.辽宁大学 经济学院,辽宁 沈阳 110036 ;2.潍坊学院 数学与信息科学学院,山东 潍坊 261061;3.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024 )
自1965年L. A. Zadeh提出模糊集概念以来,以现实世界广泛存在的模糊性为研究对象、模糊集合论为基本工具的新兴学科得到了迅速发展.
Rosenfeld[1]在模糊集的理论基础上提出模糊群的概念. Suzuki[2]引入了权的概念,从另一个角度刻画了模糊子群.付云鹏等[3-4]研究了权与模糊化拓扑、权与反模糊子群之间的关系.Atanassov[5]引入了直觉模糊集的概念.林梦雷[6]给出一个直觉模糊集为直觉模糊群的充要条件,引入直觉模糊群关于它的正规子群的诱导商集的概念.班喜光等[7-8]通过经典集合上的模糊二元运算定义了直觉模糊群并给出其两种等价定义,讨论直觉模糊群的性质.李选海等[9]研究直觉模糊群之间的关系,在直觉模糊群之间引入了同态的概念.李晓萍等[10]研究了关于T-S模的直觉模糊正规子群、超直觉模糊群,并在同态的意义下,得到了关于超直觉模糊群之间同态和同构的结果. 付云鹏等[11]通过在模糊化拓扑上定义直觉权的概念,研究了该定义下直觉权的性质,并且证明该直觉权可以导出一种直觉模糊化拓扑,进而证明了该直觉权与其所导出的直觉模糊化拓扑之间的一一对应关系.
作者在前人研究成果的基础上,以直觉模糊子群为研究对象,并以直觉模糊子群为定义域给出直觉权的定义,讨论了论文定义下的直觉权和直觉模糊子群之间的一一对应关系.
1 引理及预备知识
定义1[5]设X为一个非空经典集合,形如
A={
的3重组称为X上的一个直觉模糊集.其中:μA:X→[0,1] ,νA:X→[0,1]均为普通的模糊集;μA(x),νA(x)分别表示x属于A的隶属度和非隶属度.
令IFS(intuitionistic fuzzy set)[X]表示X上所有直觉模糊集构成的集合.
定义2[5]设X是一个非空经典集合,A,B∈IFS[X],且有下面的形式
A={
规定序及其运算如下
(1)A⊆B⟺μA(x)≤μB(x)且νA(x)≥νB(x),x∈X.
(2)A=B⟺μA(x)=μB(x)且νA(x)=νB(x),x∈X.
(3)A∩B⟺{
(4)A∪B⟺{
若{Aj|j∈J}⊆IFS[X],J为指标集,Aj={
定义3[2]设G是经典群,G上的一个直觉模糊子集A={〈x,μA(x),νA(x)〉|x∈G},如果满足
(1)μA(xy)≥min{μA(x),μA(y)},νA(xy)≤max{νA(x),νA(y)},∀x,y∈G;
(2)μA(x-1)≥μA(x),νA(x-1)≤νA(x),∀x∈G.
则称A为G上的一个直觉模糊子群.
令IFG(intuitionistic fuzzy group)[G]表示群G上的所有直觉模糊子群所构成的集合.
定理1设G是经典群,若A,B∈IFS[G],则A∩B∈IFS[G].
证明设A={〈x,μA(x),νA(x)〉|x∈G},B={〈x,μB(x),νB(x)〉|x∈G},由定义2知
A∩B={〈x,min{μA(x),μB(x)},max{νA(x),νB(x)}〉|x∈G}.
令σA∩B(x)=min{μA(x),μB(x)},τA∩B(x)=max{νA(x),νB(x)},则∀x,y∈G,有
σA∩B(xy)=min{μA(xy),μB(xy)}≥min{min{μA(x),μA(y)},min{μB(x),μB(y)}}=
min{min{μA(x),μB(x)},min{μA(y),μB(y)}}=min{σA∩B(x),σA∩B(y)}.
同理,τA∩B(xy)≤max{τA∩B(x),τA∩B(y)}.
又因为
τA∩B(x-1)=min{μA(x-1),μB(x-1)}≥min{μA(x),μB(x)}=τA∩B(x),
τA∩B(x-1)=max{νA(x-1),νB(x-1)}≤max{νA(x),νB(x)}=τA∩B(x),
因此A∩B∈IFS[G].
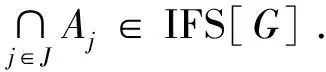
2 直觉权与直觉模糊子群
2.1 直觉权

注:定义4中直觉权的定义与文献[11]中直觉权的定义其定义方式类似,都是从一个集合到L={(α,β)∈[0,1]×[0,1],0≤α+β≤1}上满足一定条件的映射.但是定义4中映射的定义域是直觉模糊子群的集合,文献[11]中映射的定义域是模糊化拓扑的集合.另外,模糊化拓扑本质上也是一种映射,见定义5.
定义5设J:2X→[0,1],若满足
(1)J(X)=J(∅)=1;
(2)J(A∩B)≥J(A)∧J(B);
则称J为X上的模糊化拓扑.
定义6设G是经典群,G上的一个直觉模糊子集A={〈x,μA(x),νA(x)〉|x∈G},如果满足
(1)μA(xy)≥min{μA(x),μA(y)},νA(xy)≤max{νA(x),νA(y)},∀x,y∈G;
(2)μA(x-1)≥μA(x),νA(x-1)≤νA(x),∀x∈G.
则称A为G上的一个直觉模糊子群.
从定义5、6的对比可以看出直觉模糊子群并非一个模糊化拓扑.
引理1设w是G上的直觉权,∀H,K∈φ,若H⊆K,则w(H)≥w(K).
证明∀H,K∈φ,若H⊆K,则w(K)=w(〈H∪K〉)=inf{w(H),w(K)}≤w(H).
设φ={H|H≤G},A为G上的直觉模糊子群,L={(α,β)∈[0,1]×[0,1],0≤α+β≤1},定义映射wA如下
wA:φ→L,

引理2wA为直觉权.
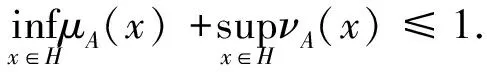
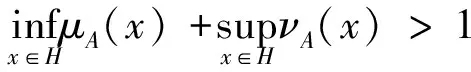
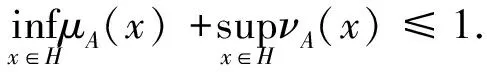
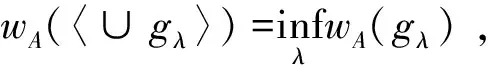
(1)
(2)
欲证(1)、(2)式相等,只需证
事实上,对于(a):∀{∪gλ}⊆φ, 则
x∈〈∪gλ〉⟹x=xλ1…xλn,xλi∈gλi,

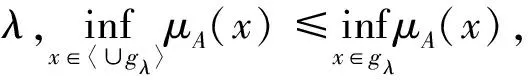
对于(b):∀{∪gλ}⊆φ,则x∈〈∪gλ〉⟹x=xλ1…xλn,xλi∈gλi,有
所以,有
所以,有
又因为
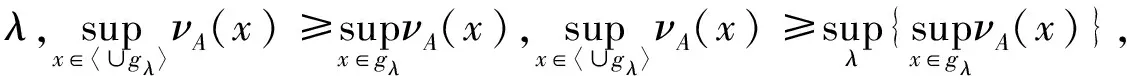
所以,有
从而wA是直觉权.
2.2 直觉模糊子群
引理3令w:φ→[0,1]×[0,1],H令则Aw={〈x,μAw(x),νAw(x)〉|x∈G}为G的直觉模糊子群.
证明(1) 0≤μAw(x)+νAw(x)≤1(显然).
(2) 往证μAw(xy)≥min{μAw(x),μAw(y)}.
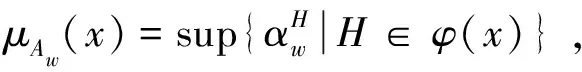
同理,∃K∈φ(y),使得μAw(xy)<α2,w(K)=(α2,β2),于是μAw(xy)<α1∧α2.

(3) 往证νAw(xy)≤max{νAw(x),νAw(y)}.
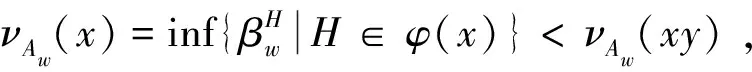
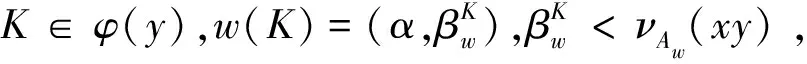
另一方面,〈H∪K〉∈φ(x)∩φ(y)⊆φ(xy),而

2.3 直觉权与直觉模糊子群的一一对应关系
定理2设A是G上的直觉模糊子群,w是G上的直觉权,则
(1)wAw=w;
(2)AwA=A.
证明(1) ∀H∈φ,往证wAw(H)=w(H).令wAw(H)=(α1,β1),w(H)=(α,β),往证α1=α,β1=β.
对∀


∀

(2) ∀x∈G,往证AwA(x)=A(x),即证μAwA(x)=μA(x),νAwA(x)=νA(x),有
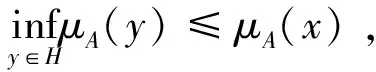
若″<″成立,则∃t∈[0,1],使得
(3)
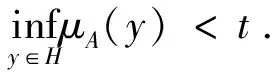
令Ht={y∈G|μA(y)>t},则Ht为G的子群.
事实上,∀x,y∈Ht,则μA(x)>t,μA(y)>t.由A为G上的直觉模糊子群,则μA(xy)≥min{μA(x),μA(y)}>t,故xy∈Ht;又因为μA(x-1)≥μA(x)>t,故x-1∈Ht.从而Ht为G的子群.
由(3)知x∈Ht,则Ht∈φ(x),所以,∃y∈Ht,使得μA(y)

