无粒子损失的W态融合研究综述

杨 名，丁成赟，臧学平

(1．安徽大学 物理与材料科学学院， 安徽 合肥 230601；2．池州学院 机电工程学院，安徽 池州 247000)

量子纠缠[1-2]是量子力学中最重要的概念之一，是实现量子信息处理不可或缺的重要物理资源，广泛应用于量子隐形传态[3]、量子超密编码[4]、量子密钥分配[5]、量子安全直接通信[6]等.两粒子纠缠态的研究已臻完善，对多粒子纠缠态(如GHZ态[7]、W态[8]等)，由于其比两粒子纠缠态有更为复杂的纠缠结构和特性，因而研究进展缓慢.同时，相对于两粒子纠缠态，多粒子纠缠态有更强的量子非局域关联[7]，在量子信息处理中更具优势.作为一类特殊的多粒子纠缠态，W态抵抗粒子损失的能力比GHZ态强大[9]，而且在量子网络匿名传输[10]和最优量子普适克隆机[11]构建中扮演重要角色.此外，由于不同多粒子纠缠态间的不等价性[8]，无法仅通过局域操作和经典通讯(LOCC)实现将某一多粒子最大纠缠态转化为不同类型的多粒子纠缠态，因此简单高效制备大规模纠缠W态显得尤为重要.

2011年，Özdemir等[12]首次提出W态的融合思想，为制备大规模的纠缠W态提供了有效途径.其基本原理为：2个或者多个小规模的纠缠W态，在只能获取每个W态中1个粒子的前提下，使这2个或多个粒子经过融合装置得到1个更大规模的纠缠W态.例如，2个任意粒子数目的最大纠缠W态为

(1)

(2)

当粒子A和B局域地经过某个融合装置后，通过选择这2个粒子的状态概率得到1个更大粒子数目的最大纠缠W态|WN+M-k〉(k=0,1或2).可以发现，若k=1或2，输出纠缠W态总粒子数目小于2个最初资源纠缠W态总粒子数目之和，称此类融合为有粒子损失的W态融合.与之相对，若k=0，目标纠缠W态总粒子数目恰好等于两个最初资源纠缠W态总粒子数目之和，称此类融合为无粒子损失(qubit-loss-free，简称QLF)的W态融合.另外，制备大规模纠缠W态的另一途径是W态的扩展[13-15]，相对于融合，W态的扩展指的是通过扩展装置将某个初始纠缠W态粒子数每次增加1个或2个，可得到1个更大规模的纠缠W态.但是，融合技术能实现多个小规模纠缠W态的同时融合，而且步骤较少，因此现阶段的大部分研究均聚焦于W态的融合.尽管很多有关W态融合的理论方案已在光学系统[12, 16-21]、腔QED系统[22-25]等量子系统中陆续提出，但目前这些W态融合方案中都存在一个问题——粒子损失，即输出纠缠W态总粒子数目小于两个最初资源纠缠W态总粒子数目之和.存在粒子损失就无法实现W态的完美融合，也导致融合效率的降低及融合步骤的增加.因此，该文将简要介绍几类重要的有粒子损失的W态融合方案及其相互关系，着重对无粒子损失的W态融合方案及其物理原理进行讨论，并给出该方向研究的总结与展望.

1 有粒子损失的W态融合

1.1 有粒子损失的光子W态融合

早期的W态融合方案多在光学系统中实现.文献[12]首次提出利用光学融合门实现W态融合的物理方案，其融合装置由1个偏振分束器(PBS)、1个半波片(HWP)和2个光子探测器组成，最终将2个光子纠缠W态|WN〉和|WM〉概率融合为1个|WN+M-2〉(N,M≥3)态.在此基础上，Bugu等[16]引入1个水平偏振的辅助光子并实施1次Fredkin门操作，最终得到的光子纠缠W态为|WN+M-1〉(N,M≥2), 减少1个粒子损失，提高了融合效率.文献[17-18]利用类似的方法分别提出了同时融合3，4个光子纠缠W态的物理方案.但这些方案均存在一定的局限性，如文献[12]的方案需最初资源纠缠态为|W3〉, 即融合之前必须通过其他方案制备这些资源；其他方案则均应用了复杂的量子逻辑门(如量子Fredkin门、量子Toffoli门等)，这些控制逻辑门在实验上很难实现，从而大大降低了方案的实验可行性.

为了克服上述方案存在的不足，研究人员提出了一些新的融合方案.2015年，Han等[19]利用弱交叉克尔非线性和线性光学元件组成的新融合装置来替代基于复杂量子逻辑门的融合装置，提高了融合方案的实验可行性，最终以较高效率制备了光子纠缠W态|WN+M-1〉.2016年，安徽大学杨名课题组[20]提出了一个基于偏振依赖分束器(PDBS)的光子纠缠W态的融合方案，该方案可以将2个W态|WN〉和|WM〉融合为1个|WN+M-1〉态，以及将3个W态|WN〉,|WM〉，|WT〉融合为1个|WN+M+T-2〉态；同时，该方案由于只涉及PDBS和光子探测器，相比较而言更加简单可行.虽然这些方案均成功规避了量子控制门，提高了实验可行性，但粒子损失问题依然存在，而存在粒子损失就无法实现W态的完美融合，导致融合效率的降低以及融合步骤的增多.

1.2 有粒子损失的原子W态融合

随着固态量子计算和量子通信的发展，原子纠缠吸引了越来越多研究人员的关注.Zang等[22-23]利用腔QED系统提出了原子纠缠W态的融合方案，其本质是用腔模和原子的大失谐相互作用代替控制门操作，而这种大失谐相互作用已被实验实现，因此提高了融合方案的可行性.Ji和Han等[24-25]分别利用量子Zeno动力学、连接氮空位(N-V)色心的微环形谐振腔(MTR)制备了|WN+M-2〉和|WN+M-1〉.同样地，虽然这些方案均提高了融合的可行性，但粒子损失问题依然存在.

2 无粒子损失的W态融合

2.1 无粒子损失的W态融合机制

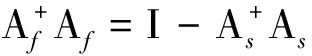
(3)

完整的2值POVM测量为联合幺正变换

UABC(|WN〉⊗|WM〉⊗|0〉C)=Af(|WN〉⊗|WM〉⊗|0〉C)+As(|WN〉⊗|WM〉⊗|1〉C)，

(4)

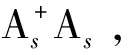
(5)

若|a0|=|a1|，则式(5)变为1个(N+M)粒子的最大纠缠W态|WN+M〉，其最大成功概率Ps=(N+M)/2NM.通过与有粒子损失的W态融合方案[12，16-18]比较，该无粒子损失的W态融合方案的资源消耗较少(见图1).

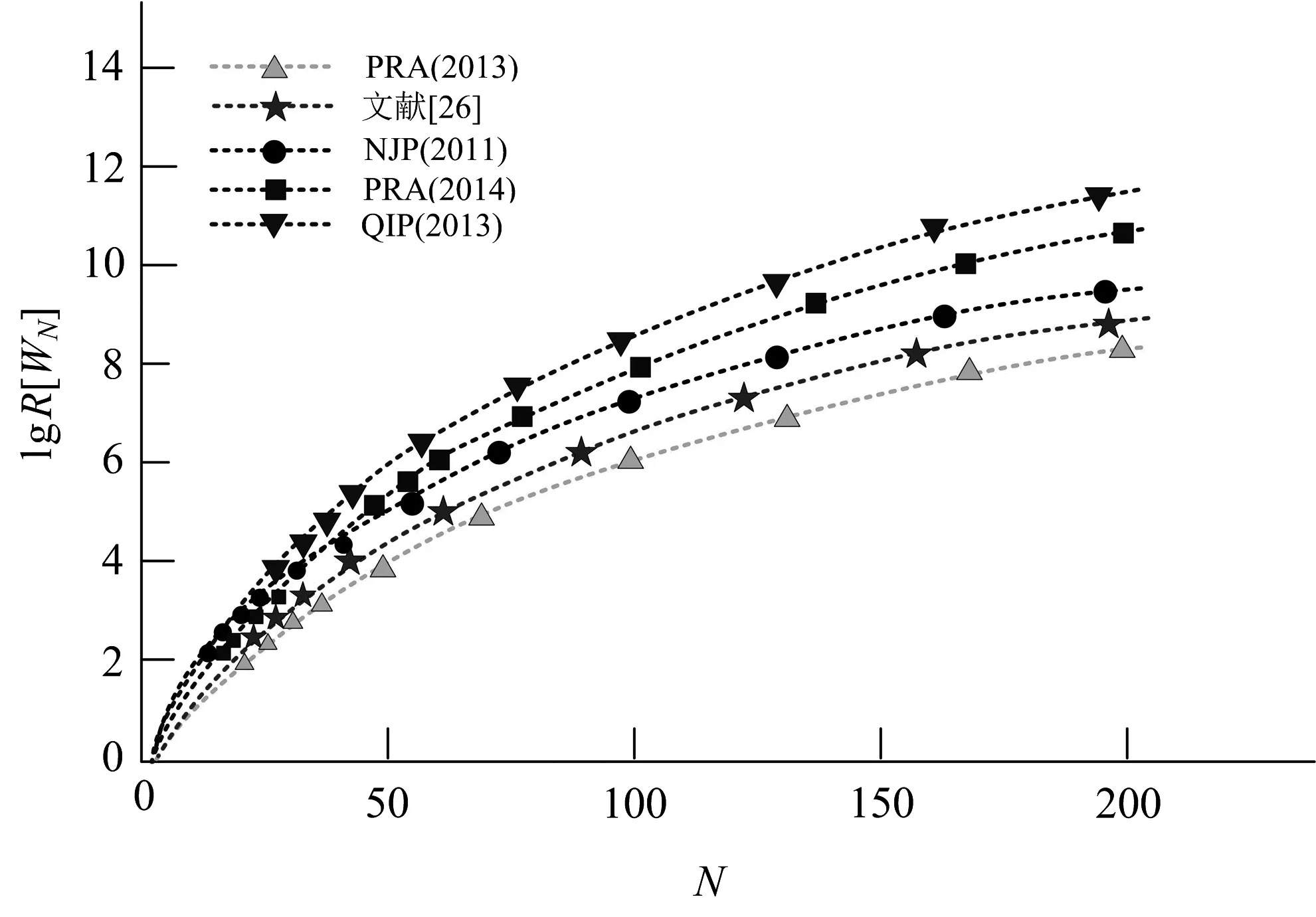
图1 文献[26]方案与其他纠缠W态融合方案的资源消耗比较

另外，上述无粒子损失的融合机制仅适用于2个小规模的纠缠W态的融合，那么3个及其以上的纠缠W态QLF融合是否也可通过类似的方案实现呢？最近，已经有研究人员提出了可融合3个W态的QLF融合机制，并在光学系统中给出了相应的物理实现方案，此方案将在下文详述.

2.2 无粒子损失的光子W态融合

基于杨名课题组提出的2个纠缠W态的无粒子损失(QLF)融合机制， Wang等[27]提出了可同时融合3个纠缠W态的无粒子损失融合机制，并在光学系统中设计了相应的物理实现方案.该方案的核心物理思想与2个W态QLF融合的基本相同，均是对从待融合的2个或3个W态中摘取的2个或3个粒子执行1个2值的POVM测量，且设计一个适当的联合幺正操作，来实现3个纠缠W态的无粒子损失融合.其成功的POVM元及幺正变换U矩阵分别为

As=a0|HHH〉〈W|+a1|W〉〈HHH|，

(6)

(7)

同理，完整的2值POVM测量为联合幺正变换

(8)

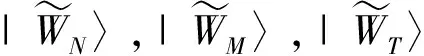
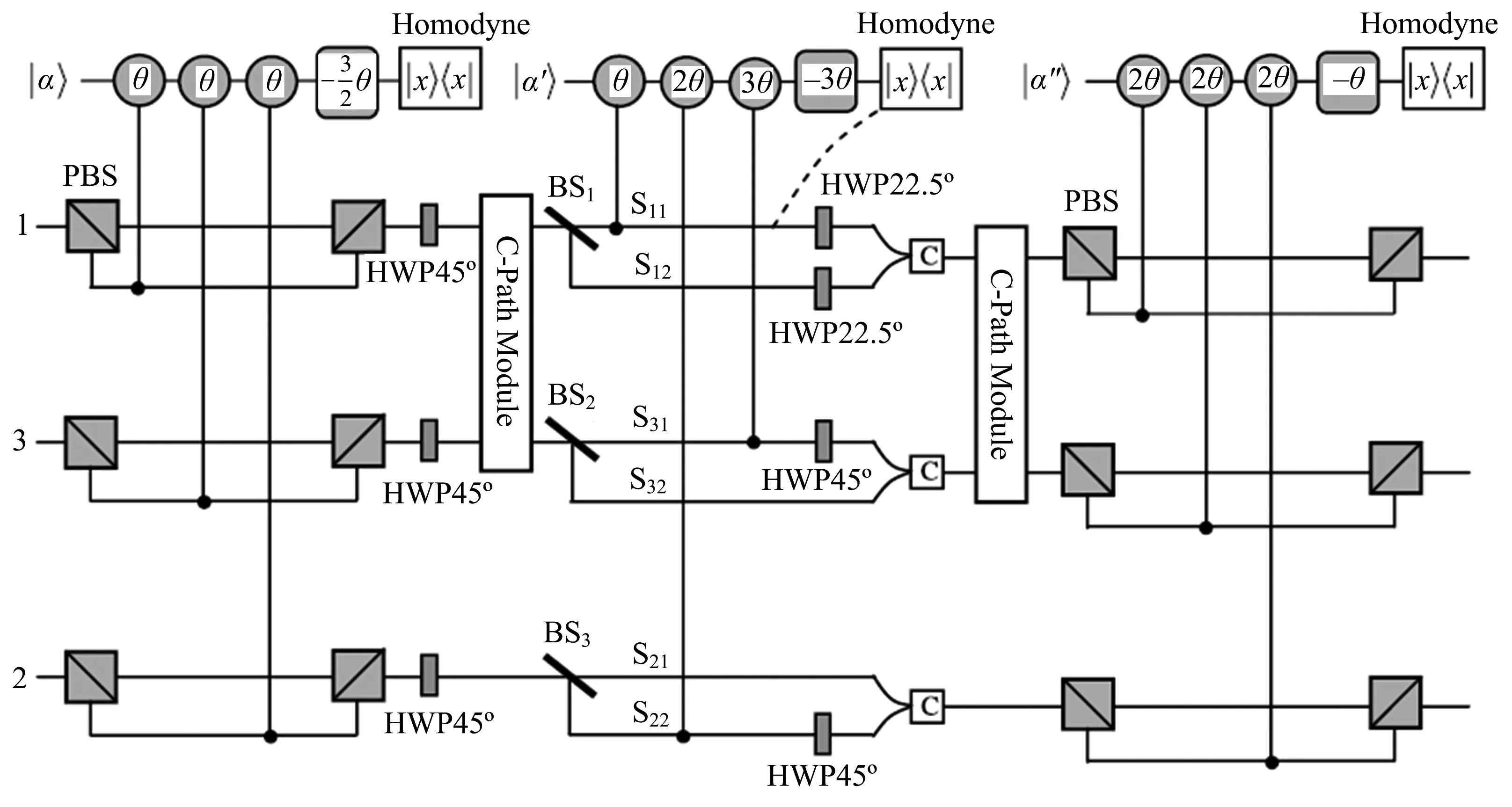
图2 文献[27]方案中3个光子纠缠W态QLF融合的光学实现过程

2.3 无粒子损失的原子W态融合

尽管杨名课题组在文献[26]中提出的2个纠缠W态的QLF融合机制可在腔QED系统中实现，但其中的辅助系统还是原子系统，并且需要测量辅助原子的状态以完成整个融合过程，而原子状态的探测在实验上较为复杂.因此，杨名课题组在文献[28]中提出了一个通过探测光子状态来实现原子纠缠W态的QLF融合物理方案.该方案的物理实质是利用原子与腔模共振相互作用及腔模状态探测，来实现无粒子损失的2个和3个原子纠缠W态的融合.该融合机制的核心为如下的原子与腔模共振相互作用

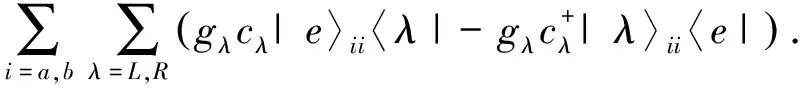
(9)

利用该相互作用哈密顿量，分别得到4个初态|R,R;R〉,|R,L;R〉,|L,R;R〉，|L,L;R〉的演化结果.每个待融合W态中只能摘取1个粒子的情况下，通过探测腔模光子状态实现原子纠缠W态的QLF融合，得到|WN+M〉，|WN+M+T〉的概率分别为4(N+M)/9NM，16(N+M+T)/81NMT.文献[28]方案与其他纠缠W态融合方案资源消耗比较如图3所示.通过资源消耗和实验可行性分析可知，该方案在当前的实验条件下是可实现的.

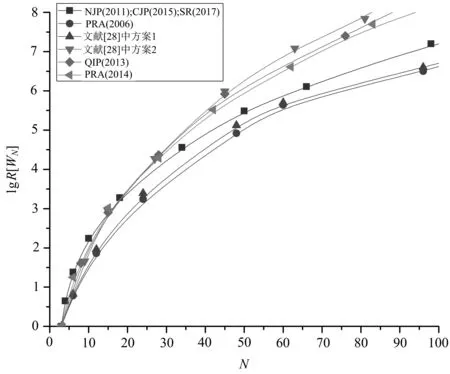
图3 文献[28]方案与其他纠缠W态融合方案资源消耗比较

3 总结与展望

纠缠W态作为一类特殊的多粒子纠缠态，是量子信息处理中的重要物理资源.由于其复杂的纠缠结构和特性，其制备进展缓慢.直到量子态融合和扩展技术出现，大规模纠缠W态制备的理论方案才被陆续提出.该文主要对W态的融合研究进行综述，着重阐述无粒子损失的W态融合.

当前的纠缠W态融合技术已取得较大发展，但有如下问题有待探索：(1)文献[26]提出的方案中，最终的成功概率为PN+M=(N+M)/2NM，但还没有达到最大概率PN+M=(N+M-1)/NM.(2)目前的所有融合方案的前提是只能从每个待融合W态中提取1个粒子，而随着实验技术的进步能够提取其中2个粒子，在此情况下，融合机制将会发生怎样的变化呢？对这2个问题的探索有可能进一步推动W态融合研究的深入.因此，后续的研究工作可围绕这2点展开.