基于扩展技术的大规模纠缠W态制备研究综述

臧学平,汪贤才

(1.池州学院 机电工程学院，安徽 池州 247000； 2.中国科学技术大学 材料科学与工程系，安徽 合肥 230026)

量子纠缠在量子通信和量子计算中有重要应用，因此量子纠缠吸引了越来越多科研人员的关注.纠缠的非局域性是量子纠缠态的典型特征，用于实现多种量子信息处理过程(如量子密集编码、密钥分配、量子密码系统等).两粒子纠缠是纠缠最简单的形式，性质也较为简单.多粒子纠缠的结构和性质较为复杂，相对两粒子纠缠其有更强的量子非局域性和稳定性，对于量子信息处理来说，多粒子纠缠更加重要.多粒子纠缠态常见的有：Greenberger-Horne-Zeilinger (GHZ)态[1]、W态[2]、Cluster态[3]等.研究表明，通过局域操作和经典通信不能实现不同类型纠缠态的相互转换，但量子信息处理过程中需要不同类型的多粒子纠缠态，如Cluster态是量子计算的基础资源[4]、GHZ态是量子隐形传态和量子密钥分配重要的传输信道[5-6]、W态对量子信息传输的安全性尤其重要等.在多粒子纠缠态中，W态具有很多特殊的性质，在量子信息处理中有广泛应用.相对于其他多粒子纠缠态，W态在对抗粒子丢失方面有显著优点[2]，在量子网络匿名传输中扮演重要角色[7].值得注意的是，通过局域操作和经典通信，可将最大纠缠两粒子态转化为任意纠缠大小的两粒子态；然而，对于多粒子纠缠，由于不同类别的多粒子纠缠态间的不等价关系，无法用同样方法将某一最大纠缠多粒子态转化为不同类型的多粒子纠缠态.因此，寻找简单有效的大规模纠缠W态的制备方法就显得格外重要.

大规模W态的制备多是通过融合与扩展技术来实现，实验已证明融合与扩展是多粒子纠缠态制备的有效途径[8-22].通过融合技术可实现从两个甚至更多个小规模的多粒子纠缠态到更大规模的多粒子纠缠态的转化，即从两个小规模的最大纠缠多粒子纠缠态中各取一个粒子，通过不同融合机制实现两个小规模多粒子纠缠态的融合[19].通过这种融合机制，还可实现从3，4个甚至更多个小规模多粒子纠缠态到大规模多粒子纠缠态的转化[20-22].

扩展技术也可制备多粒子纠缠态.扩展技术通过访问初始纠缠态的1个量子比特，且添加1个或多个量子比特，便得到更大规模的纠缠态[9-16].例如，任意粒子数目的最大纠缠W态

(1)

其中的粒子1和k个辅助粒子局域地通过扩展门相互作用后，可概率得到1个(N+k)粒子的最大纠缠W态|WN+k〉(k=1,2或n).

众所周知，多粒子的GHZ态和Cluster态原则上是通过在1个纠缠量子位和1个添加的新量子位间施加1个控制酉门而扩展得到的[23-24].W态扩展技术较复杂的原因如下：(1)通过访问N个量子位中的1个量子位来实现对N个量子位的W态扩展时，剩下的(N-1)量子位的状态必须变为适当的状态，而这取决于扩展输出的W态规模大小，因此原则上酉门不能用于W态的扩展.(2)W态的量子位两两纠缠，形成量子位的网状纠缠结构[2,25]，因此多体纠缠结构具有复杂性.为了在保持这种结构的情况下扩展为N量子位的W态，新添加的量子位不仅要与初始W态中被访问的量子位纠缠在一起，而且还必须与剩下未接触的(N-1)量子位形成独立的成对纠缠.由于原则上酉门不能用于W态扩展，故W态扩展是概率性的.该文将简要介绍几类重要的概率性的W态扩展方案及其关系，着重对W态的确定性扩展方案及其物理原理进行讨论，并给出W态扩展研究的展望.

1 W态的概率性扩展技术

1.1 从N粒子W态到(N+1)粒子W态的扩展

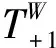
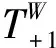
Heff=g[(a+|g1〉〈e1|+a|e1〉〈g1|)+(a+|g2〉〈e2|+a|e2〉〈g2|)].

(2)

通过控制原子飞行速度，在原子1和处于激发态的辅助原子2与真空态单模腔发生共振相互作用后探测腔场的状态，可概率实现原子W态的扩展.

1.2 从N粒子W态到(N+2)粒子W态的扩展

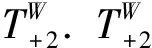
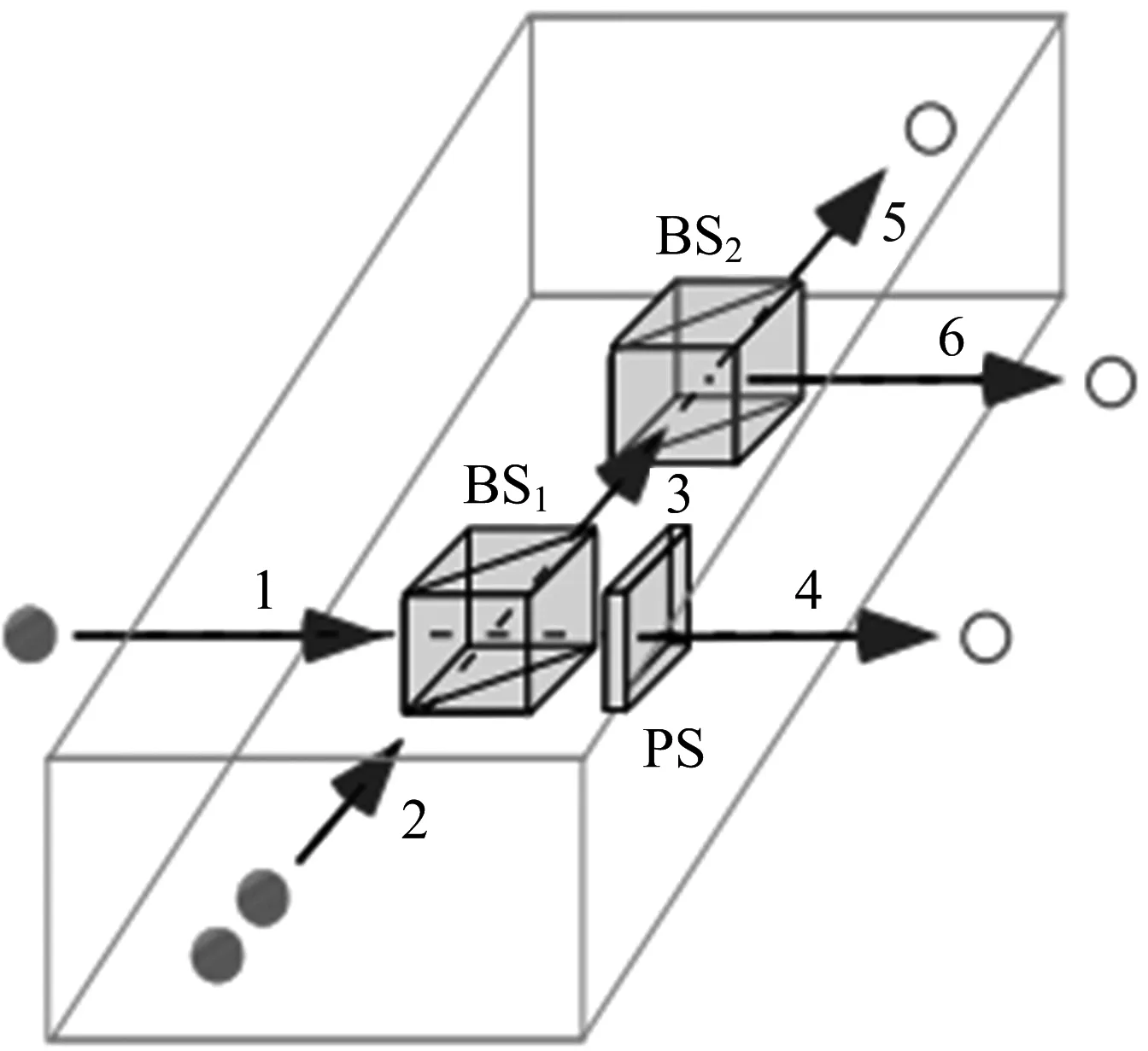
图1 文献[10]中的光子W态扩展门

图1中，式(1)中的光子1从模式1输入，并经过50∶50的分束器(BS1)与2个处于水平偏振的辅助光子混合.BS1的一个输出模式被另一个50∶50的分束器(BS2)进一步分成2种模式.当每个输出模式的4，5，6都有光子时，则扩展操作成功.相移器(PS)是在水平偏振和垂直偏振间引入π相位相移的半波片，其使输出的W态保持标准对称形式.

该扩展操作有2个基本特征：(1)输入光子和辅助光子之间是均衡的；(2)水平偏振光子从模式1进入的扩展成功概率(1/16)是垂直偏振光子从模式1进入的扩展成功概率(3/16)的1/3.利用该系统可实现从N光子W态到(N+2)光子W态的扩展.

1.3 从N粒子W态到(N+n)粒子W态的扩展

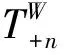
图2 文献[11]中的光子W态扩展门

图2中，在扩展方案中有由L个空间模式组成的2L输入和输出模式，每个模式有2个偏振(水平偏振和垂直偏振)模式.式(1)中光子1从空间模式1输入，n个水平偏振光子Fock态进入空间模式2，剩下的输入模式均处在真空态. 利用此扩展门能实现从N光子W态概率扩展到(N+n)光子W态.

虽然上述方案均能成功实现W态的扩展，但均只能以概率的方式得到W态 ，而概率性扩展的效率较低.因此，后续的研究工作主要集中于W态的确定性扩展技术.

2 W态的确定性扩展技术

Yesilyurt，Zang等[12，15]分别基于光学系统、腔QED系统提出了W态的确定性扩展方案. 确定性扩展包括以下几个阶段：(1)由2个独立粒子制备1个EPR态；(2)由EPR态和2个辅助粒子扩展为4粒子W态；(3)由此推广，可实现N粒子W态确定性扩展为2N粒子W态.

2.1 光子W态的确定性扩展

Yesilyurt等[12]提出了基于光学系统的W态确定性扩展方案，文献[12]中的光子W态确定性扩展门如图3所示.

图3 文献[12]中的光子W态确定性扩展门

由图3可知，此扩展门由1个controlled-Hadamard (CH)门和1个controlled-NOT (CNOT)门组成.从模1，2输入的态|a〉1|b〉2，通过扩展门后变为

(3)

其中：c=a⊕b.由式(3)知，如果输入态为|01〉12或|11〉12，则得到Bell态

或

而对于其他输入态，扩展门的变换可表示为

|00〉12→|00〉1′2′，|10〉12→|11〉1′2′.

当|0〉=|H〉，|1〉=|V〉，该扩展门可制备光子Bell态.基于光子Bell态和2个辅助水平偏振光子，利用2个扩展门可实现由光子Bell态到4光子W态的确定性扩展.依此类推可实现N光子W态到2N光子W态的确定性扩展.

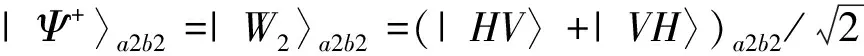
(4)

(5)

式(4)，(5)表明已实现确定性扩展.

2.2 原子W态的确定性扩展

光子W态的确定性扩展方案需要利用光学CH和CNOT门，这些光学门操作复杂，为解决上述问题，Zang等[15]提出腔QED系统W态的确定性扩展方案，该扩展方案基于原子与腔场之间的失谐相互作用，且无须测量.该确定性扩展方案中，2个全同2能级原子与单腔模发生大失谐相互作用，其哈密顿量为

(6)

图4为文献[15]中的原子W态确定性扩展门。

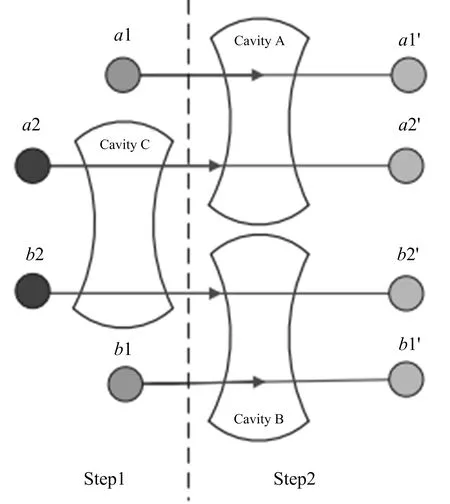
图4 文献[15]中的原子W态确定性扩展门

由图4可知，该确定性扩展的过程为：(1)将初始分别处于激发态和基态的原子a2和b2同时送入腔场C，同时控制2原子的飞行速度.基于原子与腔场的大失谐相互作用，制备的原子W态为

(7)

当原子a2和b2飞出腔场C时，执行下一步.(2)引入2个初始都处于基态的辅助原子a1和b1，并控制它们的飞行速度.原子a1，a2和原子b1，b2分别同时飞入单模腔场A和B，当4个原子飞出腔场A和B后，a1，a2、b1，b2确定性处于4原子W态

(8)

可以看出，该扩展过程无须任何测量.依此类推，相同的4个并行扩展门可将4原子W态确定性地扩展为8原子W态，原则上该方案可从分离状态的原子开始，确定性制备任何偶数个原子W态.

3 总结与展望

多粒子W态是量子信息处理重要的物理资源.由于W态纠缠结构的特殊性，其制备研究进展缓慢.直到量子态融合和扩展技术出现，大规模纠缠W态制备的理论方案才被提出.该文主要对W态的扩展技术研究进行综述，着重讨论W态的确定性扩展技术.

当前的W态扩展技术已经取得较大进展，但还有一些问题亟待深入研究：(1)目前已有的W态确定性扩展方案只能实现由N→2N粒子的W态扩展，如何实现确定性得到奇数粒子的W态值得进一步研究；(2)目前讨论的W态确定性扩展技术仅仅限于光学系统和腔QED系统，该W态确定性扩展技术能否在其他系统实现有待探索；(3)目前确定性扩展技术仅适用于W态，其他类型多粒子纠缠态是否也能确定性扩展有待研究.后续研究可围绕这几点展开.