基于Λ型原子的纠缠态融合研究综述

计彦强，赵艳君，邵晓强*

(1.东北师范大学 物理学院 量子科学中心,吉林 长春 130024；2.渤海大学 物理系，辽宁 锦州 121000)

量子纠缠是量子力学的精髓，在量子通信中处于重要位置.处于纠缠态的2个子系统无论相距多远，它们间的关联依然存在.当量子叠加态拥有2个及以上量子比特时，对其中任意一个量子进行测量，与其有关联的量子比特会塌缩到相应的状态，且测量结果与它们之间的距离无关.通过对量子纠缠态的操作，可以实现信息的存储、提取、编码、传递.因此，量子纠缠一直是量子信息研究的核心问题.纠缠态的非局域性广泛应用于量子信息中，如量子安全直接通信[1-5]、量子密钥分发[6-8]、量子隐形传送[9-11]、量子密钥共享[12-15]等.

多粒子纠缠态的量子非局域性比2粒子纠缠态的强，因此多粒子纠缠态在量子信息中应用更广.由于多粒子纠缠态的结构和特性比较复杂，随着粒子数增加，制备难度也相应增加.研究人员提出扩展和融合操作，这两种操作均能有效制备多体纠缠态.扩展操作每次使初态至多增加2个粒子，但对融合操作来说，其能使2个及以上的纠缠态进行融合，每次融合均使初始纠缠态的粒子数增加，因此，研究人员提出了一些基于融合机制制备大尺度纠缠态的方案[16-19].

原子处于激发态(高能级)是不稳定的，即使没有外界的影响，电子也会自发从激发态跃迁至低能态.原子自发辐射会降低融合方案的保真度，为了有效抑制原子的自发辐射，可以引入 Λ 型3能级原子.该文介绍纠缠态融合的概念，综述基于融合机制制备Λ型3能级原子纠缠态的几种方案，最后给出总结与展望.

1 融合机制

1.1 纠缠态融合

纠缠态的融合，是将2个大尺度的纠缠态融合产生1个更大尺度的纠缠态.例如，Alice和Bob均拥有1个大尺度多粒子的纠缠态，Alice把自身拥有的其中1个粒子A和Bob提供的粒子B均传至融合装置，融合过程只有A和B参与，剩下的粒子保持原始状态.经过一系列操作后，Claire通过测量A和B的态来判断融合是否成功.

迄今为止，研究人员在理论上已提出不同种类量子纠缠态的制备方案，如W态[20-23]、GHZ态[24-25]、EPR态[26-27]、Cluster态[28-30]等纠缠态制备方案.Özdemir 等[31]提出利用线性光学实现融合的方案，该方案能使单独的n个量子比特的W态(n≥2)和m个量子比特的W态(m≥2)融合，并产生(n+m-2)个量子比特的W态.Bugu等[32]在Özdemir等[31]提出方案的基础上，利用Fredkin门和单光子完成(n+m-1)个量子比特的W态(n≥2,m≥2)的融合.Yesilyurt等[33]提出融合4个W态的方案，利用3个CNOT门和1个Toffoli门产生(n+m+t+z-4)个量子比特的W态(n≥2,m≥2,t≥2,z≥2). Ozaydin等[34]利用1个Fredkin门和单光子融合产生(n+m+t+z-1)个量子比特的W态.

1.2 W纠缠态的融合

假设Alice有n个量子比特的|W〉A,Bob有m个量子比特的|W〉B,它们的初态分别为

(1)

整个系统的初态为

|φ0〉=|Wn〉A⊗|Wm〉B.

(2)

在|Wn〉A和|Wm〉B中分别提取1个原子，将这2个原子同时传至融合装置，经一系列操作后，Claire接收Alice和Bob传来的2个原子，这2个原子存在4种可能的状态(|0102〉，|0112〉，|1102〉，|1112〉),幺正演化后在输出装置中仍可探测到这4种状态.根据测量结果可判断纠缠态的融合是否成功.若测量结果为|0102〉,则融合过程失败，失败概率Pf(Wn,Wm)=P00=1/mn.若测量结果为|1112〉,则融合过程失败，失败的概率Pf(Wn,Wm)=P11=(n-1)(m-1)/mn.若测量结果为|0112〉或|1102〉,则融合过程成功，成功概率Ps(Wn,Wm)=(n+m-2)/mn.

1.3 GHZ纠缠态的融合

假设Alice拥有n个量子比特的GHZ态，Bob拥有m个量子比特的GHZ态，利用纠缠态|GHZm〉A和纠缠态|GHZn〉B融合产生1个更大的GHZ态.

Alice和Bob拥有的GHZ态分别为

(3)

整个系统的初态为

|ψ0〉=|GHZm〉A⊗|GHZn〉B.

(4)

Claire接收Alice和Bob传来的2个原子，这2个原子有4种可能状态(|0102〉，|0112〉，|1102〉，|1112〉),幺正演化后在输出的装置中仍然可以测量到这4种状态.通过测量结果可判断纠缠态的融合是否成功.|00〉或|11〉成功融合产生GHZ态的概率为1/4，|01〉或者|10〉成功融合产生GHZ态概率也是1/4.由于实际纠缠态融合过程中，需要对2个原子进行测量，所以最后融合产生的大尺度GHZ态中会少2个粒子.

2 基于Λ型原子的纠缠态融合

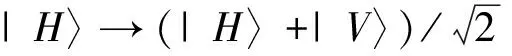
|1V〉1|1V〉2,|1H〉1|1V〉2,|1V〉1|1H〉2,|1H〉1|1H〉2.

测到它们的概率分别为

1/mn,(n-1)/mn,(m-1)/mn,(n-1)(m-1)/mn.

输出装置中测到的光子态为

HWP和PBS的联合作用使输入光子态产生如下转化

|1H〉1|1H〉2→|0〉3|1H1V〉4,|1V〉1|1V〉2→|1H1V〉3|0〉4,

|1H〉1|1V〉2→|1H〉3|1H〉4,|1V〉1|1H〉2→|1V〉3|1V〉4.

通过分辨光子1和2所处的纠缠态可判断融合过程是否成功.

下面介绍利用单腔、双腔实现Λ型原子W态的融合，以及利用Rydberg原子反封锁效应实现多粒子大尺度W态和GHZ态的融合[35-36].

2.1 基于单腔的W态融合

基于单腔的W态融合，主要利用2个束缚在光腔中的Λ型原子来实现.原子-腔系统模型和原子的能级结构如图1所示.

图1 原子-腔系统模型(A)和原子的能级结构(B)

图1B中，|g1〉和|g0〉为基态，|e〉为激发态.|g1〉↔|e〉由拉比频率为Ωj的经典场驱动，λj为原子与腔模耦合的强度.失谐量Δ远离共振时，原子与腔场及经典激光场无能量交换.相互作用绘景中，系统的Hamilton量(ћ=1)为

(5)

其中：a表示腔场的湮灭算符.

将量子比特信息编码在基态|g0〉和|g1〉上,得到4种状态(|g0g1〉,|g0g0〉,|g1g0〉,|g1g1〉).若腔场处于真空态，则4个初态的演化如下

(6)

基于量子Zeno动力学[37]可将|Wn〉A和|Wm〉B融合产生大尺度的WAB态.分别在|Wn〉A,|Wm〉B中提取的原子1，2的态为

(7)

将这2个原子同时放至真空腔进行融合，此时系统的初态为|φ0〉=|Wn〉A⊗|Wm〉B⊗|0c〉,t=Δπ/(2Ω2)时，系统演化为

(8)

Claire通过对这2个原子的测量结果来判断融合是否成功.若测量结果为|g0g0〉,则融合过程失败，失败概率Pf(Wn,Wm)=P00=1/mn.若测量结果为|g1g1〉,则这个融合还没有结束，由于Claire对原子的测量导致各自的W态粒子减少，剩下的W态会继续下一次融合，这种融合的失败概率为

Pf(Wn,Wm)=P11=(n-1)(m-1)/mn.

若测量结果为|g1g0〉,则剩下的原子态为

Alice对自己的1个原子进行单比特相位门操作

|g0〉→|g0〉,|g1〉→i|g1〉，

则剩余的原子态变为

这种融合的成功概率Ps(Wn,Wm)=(n+m-2)/(2mn).若测量结果为|g0g1〉,则融合的成功概率Ps(Wn,Wm)=(n+m-2)/(2mn).由上可知，融合的总成功概率为(n+m-2)/(mn).

2.2 基于双腔的W态融合

采用2个分离的腔，二者由光纤连接，其中一个腔控制m个Wm态原子，另一个腔控制n个Wn态原子，那么就可在这两个独立的腔中实现W态的融合.图2为基于双腔的W态融合过程.

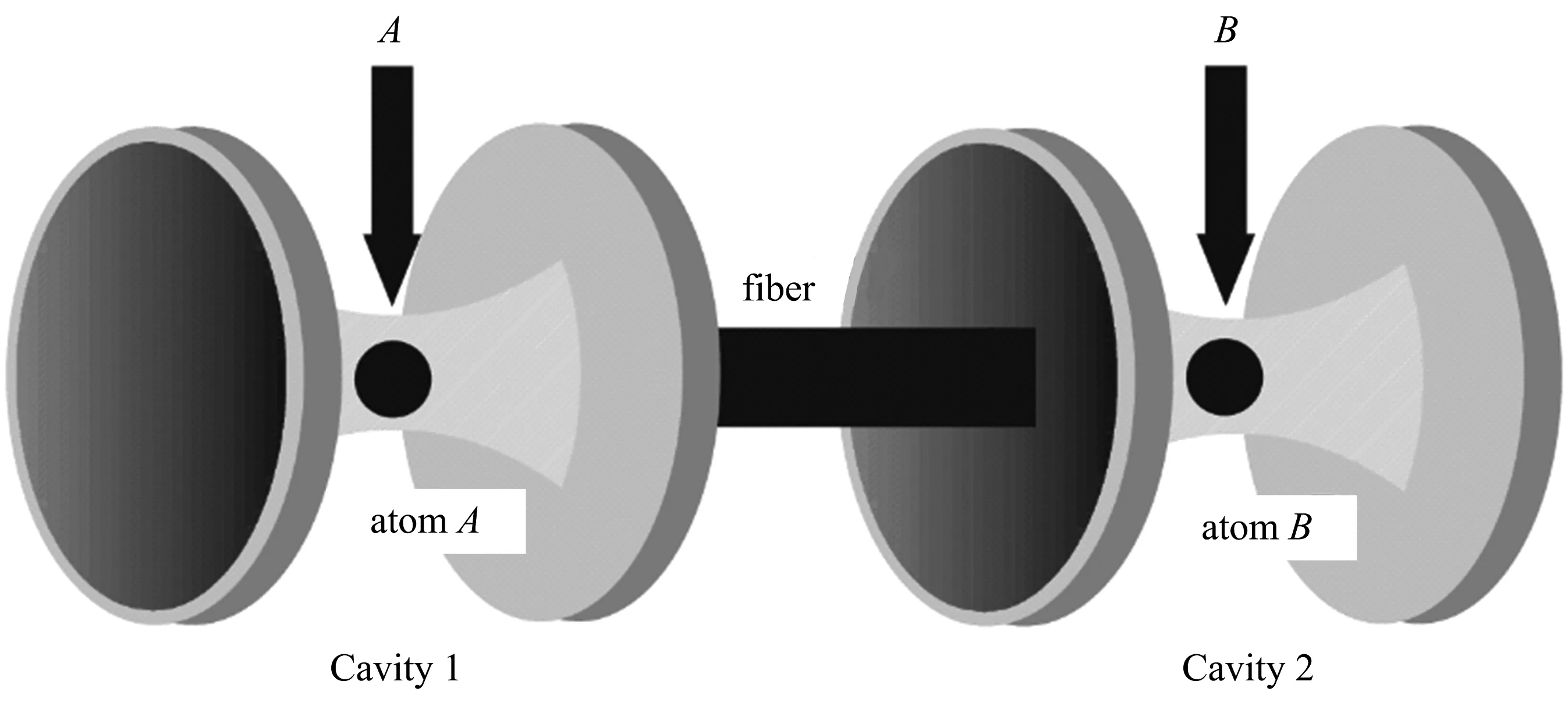
图2 基于双腔的W态融合

图2中，原子A束缚在腔1中，原子B束缚在腔2中, 腔1，2间用光纤耦合.在Lτ/(2πc)≪1[38-39]情况下，系统的哈密顿量(ћ=1)为

(9)

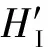
|g0g0〉|0c1〉|0c2〉|0f〉→|g0g0〉|0c1〉|0c2〉|0f〉,

|g1g1〉|0c1〉|0c2〉|0f〉→|g1g1〉|0c1〉|0c2〉|0f〉.

(10)

若测量结果为|g0g0〉,|g1g1〉,则融合失败，失败概率分别为Pf(Wn,Wm)=P00=1/mn,Pf(Wn,Wm)=P11=(n-1)(m-1)/mn.若测量结果为|g1g0〉或|g0g1〉,则融合成功，成功概率Ps(Wn,Wm)=(n+m-2)/(2mn).两个腔实现纠缠态融合的总成功概率为(n+m-2)/(mn).

实验中无论是双腔还是单腔， Λ 型原子W 态融合过程均受腔场的衰减(κ)和原子自发辐射(γ)的影响.利用 Lindblad 主方程[40]，可分析κ和γ对融合的影响.数值模拟结果表明t=Δπ/(2Ω2)时，保真度较高，且其对κ和γ的衰减具有鲁棒性.

2.3 基于Rydberg原子的 W 态融合

Rydberg封锁效应[41-42]是实现中性原子处理量子信息的机制之一.在特定条件下，即当驱动激光场频率与原子跃迁频率的失谐量与Rydberg相互作用强度满足一定的关系时，偶极封锁效应消失，这种现象被称为Rydberg 反封锁效应.Rydberg反封锁效应[43-47]在量子逻辑门实现及纠缠态制备中具有重要作用.

图3为2个Rydberg原子的能级结构，其中|r〉为Rydberg态，|0〉和|1〉为2个基态，Δrr为2个|r〉间的相互作用强度，|0〉↔|r〉间的跃迁由Rabi频率为Ωa的经典激光场驱动，|1〉↔|r〉间的跃迁由Rabi频率为Ωb的经典激光场驱动，Δa(b)表示相应的失谐量.

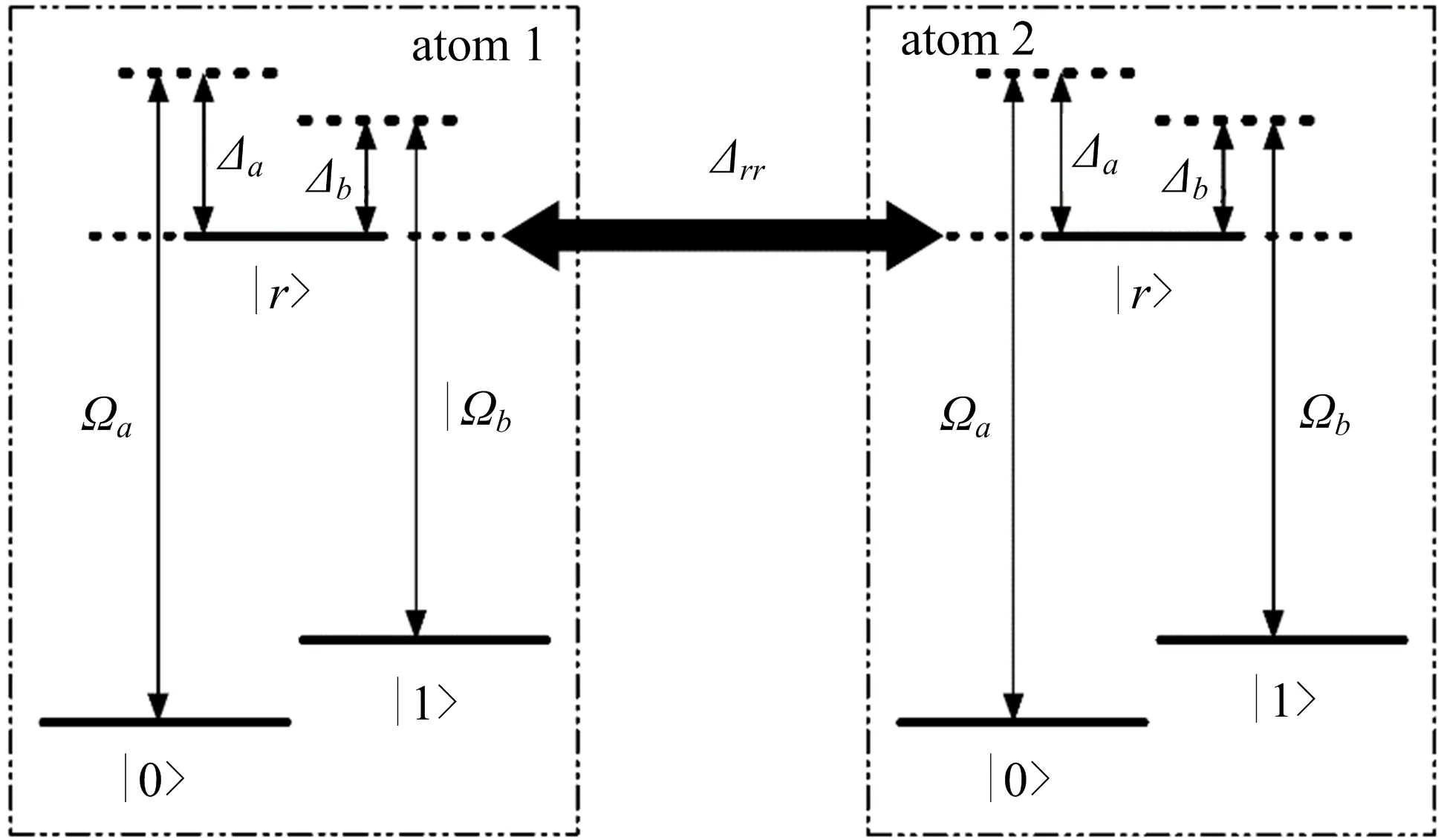
图3 2个Rydberg原子的能级结构

相互作用绘景下系统的哈密顿量为

(11)

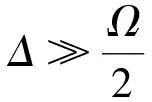
Alice和Bob拥有的多粒子态分别为

(12)

此时系统的初态为|Wm〉A⊗|Wn〉B,t=Δπ/Ω2时，Claire对原子进行测量，若测量结果为|00〉或|11〉,则融合失败，失败概率分别为Pf(Wn,Wm)=P00=1/mn,Pf(Wn,Wm)=P11=(n-1)(m-1)/mn.若测量结果为|10〉,则融合成功，成功概率Ps(Wn,Wm)=(m+n-2)/(2mn).若测量结果为|01〉,则融合成功，成功概率Ps(Wn,Wm)=(m+n-2)/(2mn).由上可知，融合的总成功概率为(m+n-2)/(mn).

2.4 基于Rydberg原子的GHZ态融合

Alice和Bob拥有的纠缠态 (m,n≥3)分别为

(13)

系统初态为|GHZm〉A⊗|GHZn〉B,在激光场驱动和原子间相互作用下，系统演化为

(14)

测量可能的结果为|00〉,|11〉,|01〉,|10〉,测量后系统状态分别塌缩为 |ψ2〉,|ψ3〉,|ψ4〉,|ψ5〉, 它们的表达式为

(15)

|ψ2〉，|ψ3〉，|ψ4〉，|ψ5〉均可通过执行单比特的相位门转变成标准的(m+n-2)个比特的GHZ态.Claire测得这4个态的概率均为1/4，因此GHZ态融合的总成功概率为1，此表明Rydberg原子反封锁效应在GHZ态融合过程具有不可替代的作用.利用Rydberg原子的反封锁效应实现GHZ态的融合，其保真度能达到99.4%.

3 总结与展望

该文综述了基于Λ 型原子实现大尺度 W 态和 GHZ 态的多粒子融合方案.利用单腔、双腔实现 Λ 型原子 W 态融合方案与利用 Rydberg 原子反封锁效应实现多粒子大尺度W 态和 GHZ 态的融合方案的保真度均超过 99%，且对κ和γ的衰减均具有鲁棒性.但是，融合方案存在不足之处：随着粒子数增加，W 态融合的成功概率降低.利用 Fredkin 同时对3个 W 态进行融合，可得到3量子比特的逻辑门，但3量子比特的逻辑门实验上并不容易实现.利用量子点-腔耦合系统实现了光子 W态的融合，由于融合操作复杂无法在实验上实现.采用腔 QED 技术实现纠缠态融合，只需控制系统的演化时间即可完成纠缠态的融合，遗憾的是该技术仅对2个纠缠态进行了融合.后续的研究目标可为：如何能同时融合多个纠缠态？通过引入什么样的辅助系统才能提高纠缠态融合的成功概率？