小R-投射模
王永铎,李 霞
(兰州理工大学 理学院,甘肃 兰州 730050)
在本文中,R都是有单位元的结合环,所有的模都是右R-模.设M和N是右R-模.称M是N-投射模,如果每个M到N的商模的右R-模同态可以提升到M到N的右R-模同态.称M是R-投射模,如果M是RR-投射的.称M是投射模,如果M对任意右R-模N是N-投射的.受到文献[1-5]的启发,本文很自然的引入小N-投射模和小R-投射模的概念.设M和N是右R-模.称M是小N-投射模,如果对于每个满同态f:N→N/N1(N1是N的任意小子模)和每个同态g:M→N/N1,存在同态h:M→N使得fh=g.称模M是小R-投射模,如果M是小RR-投射的.本文研究了小N-投射模和小R-投射模的基本性质,探讨了它们与已知模类的关系.证明了环R是半本原环当且仅当每个R-模是小R-投射模.本文也引入了小R-投射盖的概念.称满同态f:P→M或P是M的小R-投射盖,如果P是小R-投射模且f是小的满同态.证明了R是半完备环当且仅当R/J(R)是半单的且每个单R-模有小R-投射盖;R是右完备环当且仅R/J(R)是半单的且每个半单R-模有小R-投射盖.
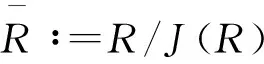
定义1设M和N是右R-模.称M是小N-投射模,如果对于每个满同态f:N→N/N1(N1是N的任意小子模)和每个同态g:M→N/N1,存在同态h:M→N使得fh=g.称M是小R-投射模,如果M是小RR-投射的.
例11) 设R是半本原环.则每个右R-模M是小R-投射模.
证明由R是半本原环知J(R)=0.对满同态f:R→R/0和同态g:M→R/0,考虑交换图,如图1所示.

图1 交换图Fig.1 Commutative diagram
因为R/0≃R是投射模,所以f可裂,即存在同态h:R/0→R使得fh=1R/0.因此存在同态hg:M→R,使得f(hg)=(fh)g=1R/0g=g.
2)Z-模Z/nZ(n≠0,1)是小Z-投射模但不是Z-投射模.
证明由J(Z)=0,知每个右Z-模M是小Z-投射模,因此Z/nZ(n≠0,1)是小Z-投射模.下证Z/nZ(n≠0,1)不是Z-投射模.因为nZ不是Z的直和项,所以短正合列0→nZ→Z→Z/nZ→0不可裂.故Z/nZ(n≠0,1)不是Z-投射模.
命题1设R是环,N是右R-模.则以下几条成立:
1) 若N是hollow模,则小N-投射模是N-投射模;
2) 若rad(N)≪N且N/rad(N)是小N-投射模,则N是半平坦模;
3) 若N是半平坦模,则每个R-模M是小N-投射模;
4)R-模⊕i∈IMi是小N-投射模当且仅当Mi(i∈I)是小N-投射模.
证明1) 根据hollow模的定义即知.
2) 由rad(N)≪N且N/rad(N)是小N-投射模,知存在同态h:N/rad(N)→N,使图2可换.
进而可知rad(N)是N的直和项,因此rad(N)=0,即N是半平坦模.
3) 因为N是半平坦模,所以rad(N)=0.再由文献[6]中命题16.7知要证M是小N-投射模,即
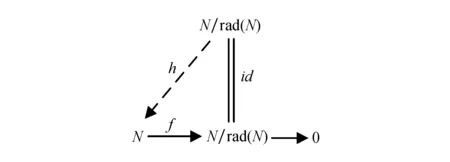
图2 交换图Fig.2 Commutative diagram
证每个同态h:M→N/0可通过自然满同态π:N→N/0分解.下证每个同态h:M→N/0可通过自然满同态π:N→N/0分解.因为自然满同态π:N→N/0是同构,所以存在同态g:N/0→N使得πg=1N/0.故存在同态gh:M→N使得π(gh)=(πg)h=1N/0h=h,即证.
4) “⟹”设右R-模M=⊕i∈IMi是小N-投射模.对满同态β:N→N/N1(N1是N的任意小子模)和同态φ:Mi→N/N1(i∈I),考虑交换图,如图3所示.
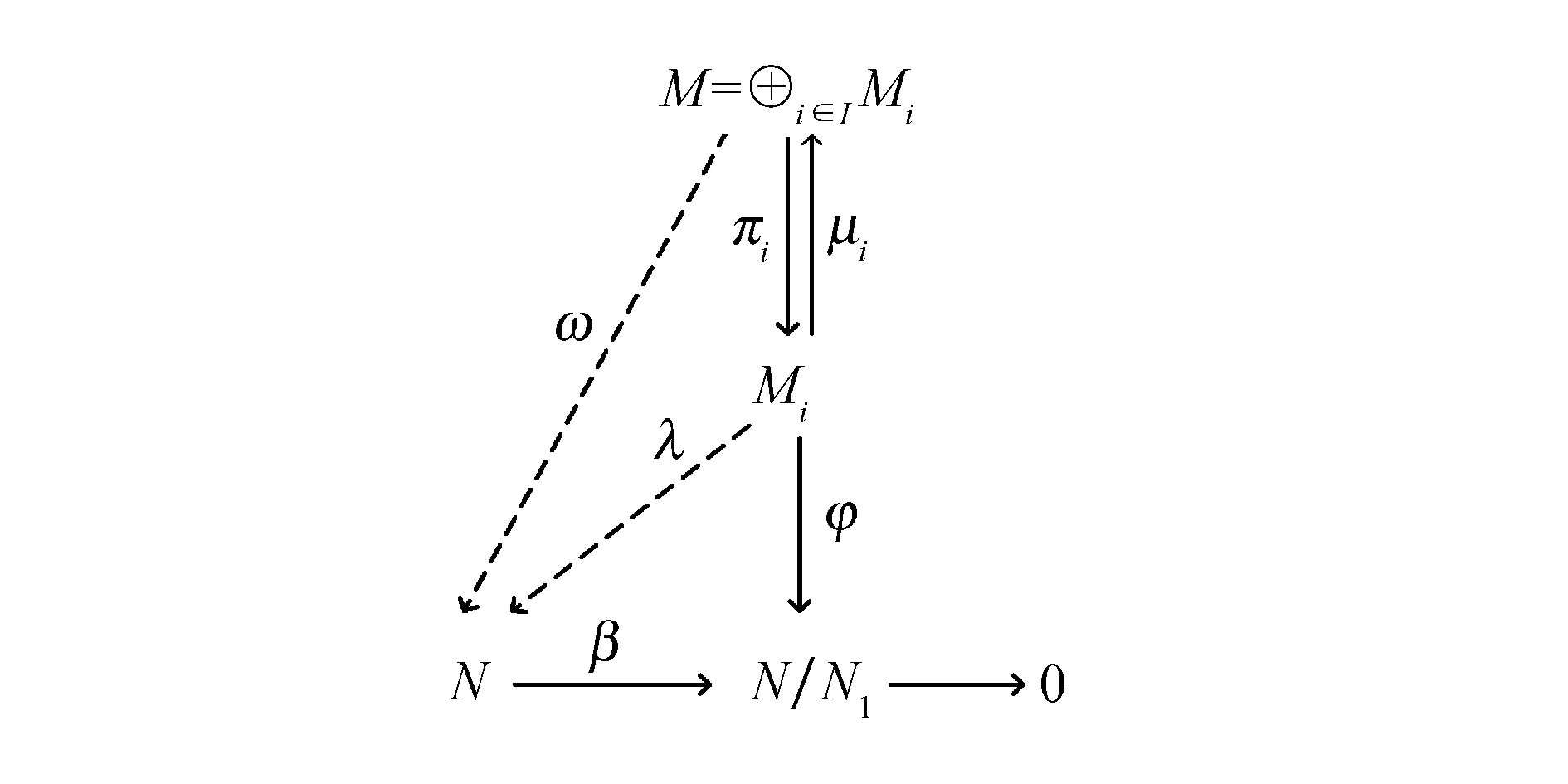
图3 交换图Fig.3 Commutative diagram

“⟸”设Mi(i∈I)是小N-投射模.对满同态β:N→N/N1(N1是N的任意小子模)和同态φ:M→N/N1,考虑交换图,如图4所示.

图4 交换图

命题2设R是环,M和N是右R-模.则以下两条等价:
1)M是小N-投射模;
2) 对N的任意小子模N1,由满态f:N→N/N1所诱导的同态f*:HomR(M,N)→HomR(M,N/N1)是满态.
证明1)⟹2) 设M是小N-投射模,N1是N的任意小子模,f:N→N/N1是满同态,g∈HomR(M,N/N1).因为M是小N-投射模,所以存在同态h:M→N,使得f*h=fh=g,故f*是满态.
2)⟹1)显然.
命题3局部环R上的右R-模M是小R-投射模当且仅当M是R-投射模.
证明“⟹”因为R是局部环,所以它有唯一极大理想J(R)且J(R)是R的小理想.由R是有限生成的,知R的每个真理想都包含在极大理想J(R)中,从而R的每个真理想都是小理想.因此小R-投射模M也是R-投射模.
“⟸”显然.
推论1局部环R上的有限生成的小R-投射模M是投射模.
证明由命题3和文献[8]中的定理2.1可知.
命题4设N是右R-模.若rad(N)≪N且N/rad(N)是半单的,则每个小N-投射模M是rad-N-投射模.
证明由rad(N)≪N且M是小N-投射的知每个同态f:M→N/rad(N)可提升到同态g:M→N.又因为N/rad(N)是半单的,由文献[5]中的命题3.14可知,M是rad-N-投射模.
推论2设R是半完备环.若右R-模M满足rad(M)≪M且M是小R-投射模,则M是投射模.
证明由R是半完备环,知R/J(R)是半单的.又因为J(R)≪R且M是小R-投射模,所以M是rad-投射模.再由rad(M)≪M和文献[5]中的定理4.7知M是投射模.
注1小R-投射模的子模不一定是小R-投射模.当环R=Z/p2Z时(其中p为素数),R是小R-投射模但它的非零理想pZ/p2Z≃R/pZ/p2Z不是小R-投射模.因为pZ/p2Z≪R不是R的直和项,所以不存在h:R/pZ/p2Z→R,使图5可换.
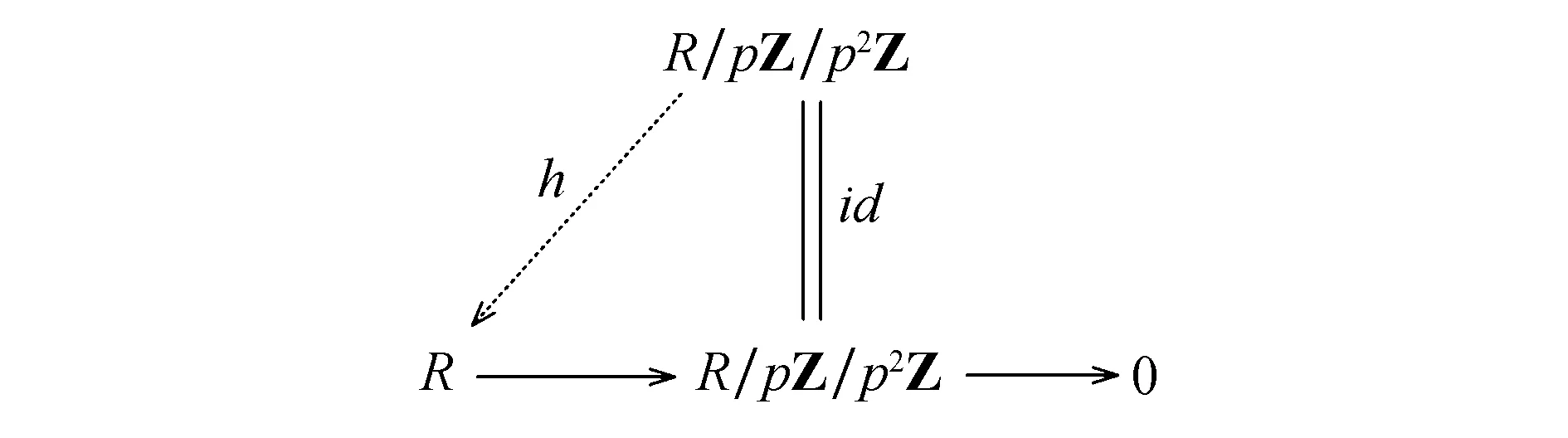
图5 交换图
定理1设R是环,M是右R-模.则以下几条等价:
1) 每个小E(M)-投射模的子模是小E(M)-投射模;
2) 每个投射模的子模是小E(M)-投射模;
3)R的每个右理想是小E(M)-投射模;
4)E(M)/E1(M)(E1(M)是E(M)的任意小子模)是内射模.
证明1)⟹2)⟹3)显然.
3)⟹4)设I是R的右理想.考虑交换图,如图6所示.

图6 交换图Fig.6 Commutative diagram
其中i:I→R为嵌入映射.因为I是小E(M)-投射模,所以存在同态θ:I→E(M)使得ηθ=f.由E(M)是内射模,知存在同态λ:R→E(M)使得λ|I=θ.又因为ηλ|I=ηθ=f,所以同态ηλ:R→E(M)/E1(M)是f的扩张,故E(M)/E1(M)是内射模.
4)⟹1) 设B是小E(M)-投射模且A是B的子模.考虑交换图,如图7所示.

图7 交换图
因为E(M)/E1(M)是内射模,所以f可以扩张到同态θ:B→E(M)/E1(M).又因为B是小E(M)-投射模,所以存在λ:B→E(M)使得ηλ=θ.因此存在同态g=λi:A→E(M),使得对任意x∈A有ηg(x)=ηλi(x)=ηλ(x)=θ(x)=f(x),故A是小E(M)-投射模.
推论3设M是内射R-模.则以下几条等价:
1) 每个小M-投射模的子模是小M-投射模;
2) 每个投射模的子模是小M-投射模;
3)R的每个右理想是小M-投射模;
4)M/M1(M1是M的任意小子模)是内射模.

定理2设R是环.则以下几条等价:
1)R是半本原环;
2) 每个右R-模是小R-投射模;
3) 每个有限生成的右R-模是小R-投射模;
4) 每个右R-模R/I(I是R的任意小右理想)是小R-投射模;
5) 右R-模R/J(R)是小R-投射模.
证明1)⟹2) 由例1可知.
2)⟹3)⟹4)⟹5)显然.
5)⟹1)因为R/J(R)是小R-投射模,所以存在g:R/J(R)→R使图8可换.
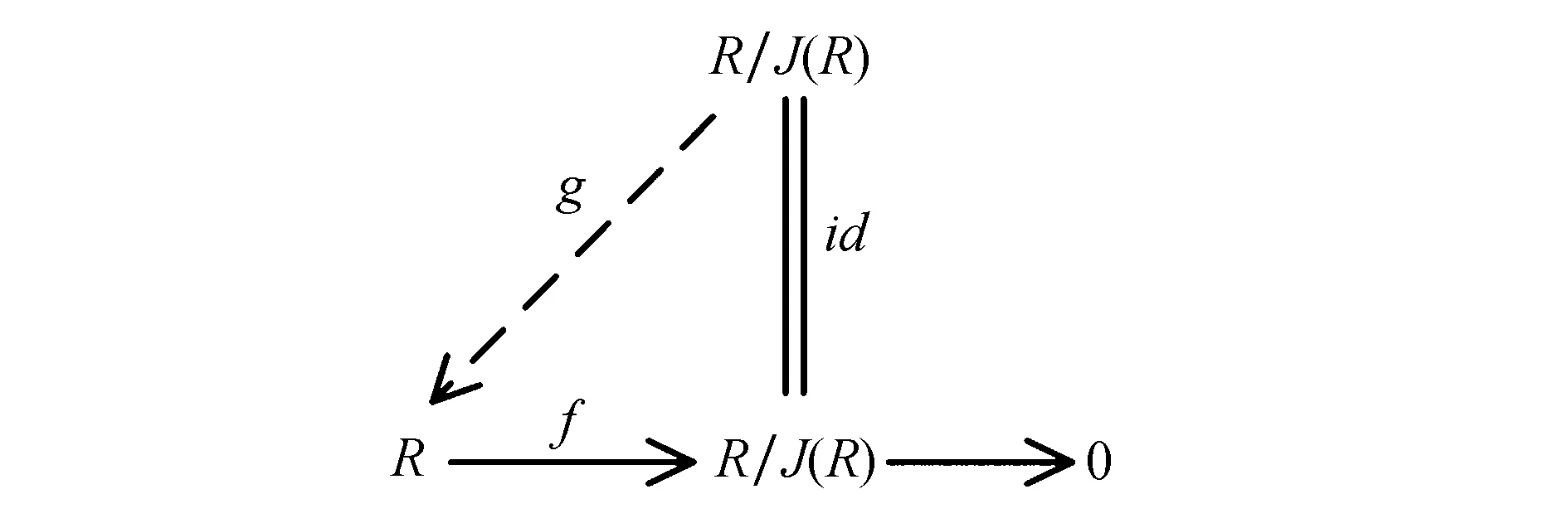
图8 交换图8Fig.8 Commutative diagram 8
进而可知J(R)是R的直和项,故J(R)=0.因此R是半本原环.
推论4若R是有限余生成的且R/J(R)是小R-投射模,则R是半单环.
证明因为R/J(R)是小R-投射模,所以J(R)=0.再由R是有限余生成的和文献[10]中的21.14可知,R是半单环.
命题6设R是环,τ是预根且τ(R)=0.如果M是小R-投射模,那么M/τ(M)是小R-投射模.
证明设M是小R-投射模.对同态f:M/τ(M)→R/I(I是R的任意小右理想)和满同态η:R→R/I,考虑交换,如图9所示.

图9 交换图Fig.9 Commutative diagram
其中π:M→M/τ(M)是自然满同态.由M是小R-投射模知存在同态g:M→R使得fπ=ηg.因为g(τ(M))⊆τ(R)=0,所以τ(M)⊆Ker(g),故存在态射h:M/τ(M)→R,使得hπ=g.又因为ηhπ=ηg=fπ且π是满同态,所以ηh=f.因此M/τ(M)是小R-投射模.
定义2设R是环,M是右R-模.称满同态f:P→M或P是M的小R-投射盖,如果P是小R-投射模且f是小的满同态(即Kerf≪P).
注2众所周知,R是半完备环当且仅当每个有限生成的R-模有投射盖,R是右完备环当且仅当每个R-模有投射盖.但每个有限生成的R-模有小R-投射盖,R不一定是半完备环; 每个R-模有小R-投射盖,R不一定是右完备环.例如每个有限生成的阿贝尔群有小Z-投射盖,但Z不是半完备环;每个阿贝尔群有小Z-投射盖,但Z不是右完备环.
定理3设R是环.则以下几条等价:
1)R是半完备环;
2)R/J(R)是半单的且每个有限生成的R-模有小R-投射盖;
3)R/J(R)是半单的且每个单R-模有小R-投射盖.
证明1)⟹2)⟹3)显然.
3)⟹1)因为R/J(R)是半单的且每个单R-模有小R-投射盖,所以每个单R-模有rad-投射盖.再由文献[3]中定理18可知R是半完备环.
定理4设R是环.则以下几条等价:
1)R是右完备环;
2)R/J(R)是半单的且每个R-模有小R-投射盖;
3)R/J(R)是半单的且每个半单R-模有小R-投射盖.
证明1)⟹2)⟹3)显然.
3)⟹1)由定理3知R是半完备的.设M是半单R-模,f:P→M是M的小R-投射盖.由文献[11]中的推论9.1.5可知,rad(P)=f-1(0)=Kerf≪P.再由推论2知P是投射的,即证.
定理5设g:P→M/rad(M)→0是M/rad(M)的投射盖.若M是小P-投射模,则M=N⊕K,其中N是投射模,K是rad(M)的子模,N∩rad(M)≪N.特别地,若rad(M)≪M,则M是投射模.
证明对满同态g:P→M/rad(M)和自然满同态η:M→M/rad(M),考虑交换图,如图10所示.
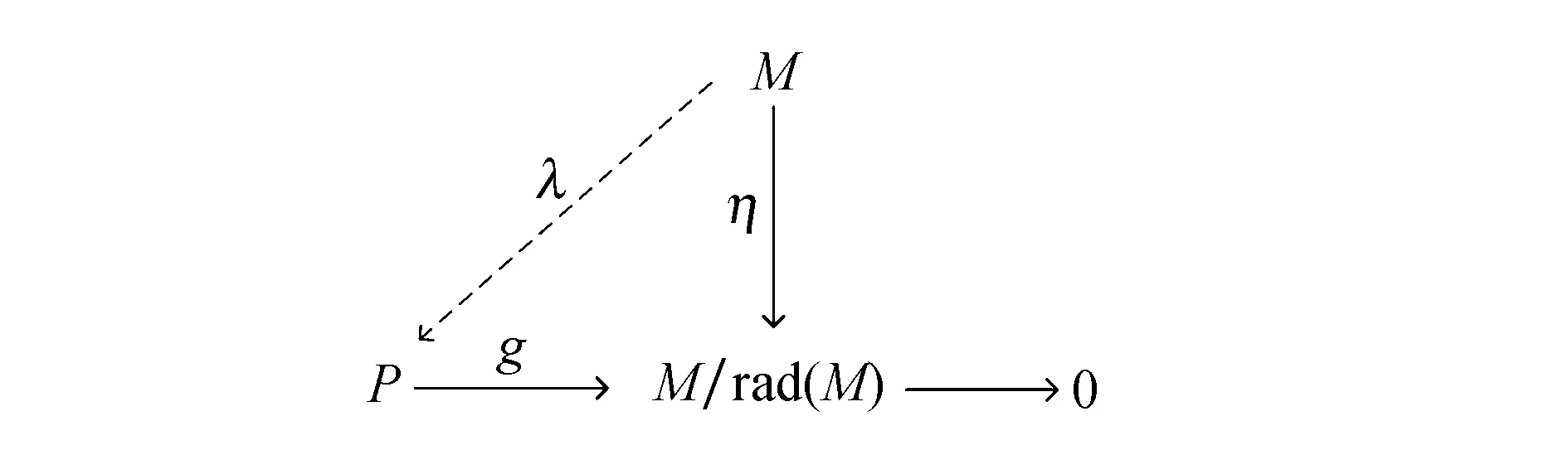
图10 交换图Fig.10 Commutative diagram


