τ-C11模的直和分解*

李煜彦

(陇南师范高等专科学校数信与信息科学学院,742500,甘肃省陇南市)

0 引言及预备知识

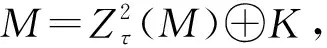
本文中的挠理论均指遗传挠理论,环是有单位元的结合环,模指酉右R-模.设M是模,称L是M的τ-全不变子模,如果L是M的全不变子模且L∈Dτ(M).称L是M的τ-基本子模,如果L是M基本子模且L∈Dτ(M).用L≤M,L≤τ-dM,L≤τ-eM和L◁τ-dM分别表示L是M的子模,τ-稠密子模,τ-基本子模和τ-全不变子模.称M是C11模,如果对M的任意子模L,存在M的直和项K,使得K是L在M中的补.称M是τ-C1模,如果对M的任意τ-稠密子模N,存在M的直和项K,使得N≤τ-eK.称M是τ-FI-extending模,如果对M的任意τ-全不变子模N,存在M的直和项K,使得N≤τ-eK.

定义1[10]令Zτ(M)={m∈M|ann(m)≤τ-eRR}={m∈M|∃L≤τ-eRR,mL=0}.称Zτ(M)是M的τ-奇异子模.若Zτ(M)=M,则称M是τ-奇异模.若Zτ(M)=0,则称M是τ-非奇模.

由文献[10]知,Zτ(M)满足如下等式

Zτ(M)=Z(M)∩τ(M)=τ(Z(M))=Z(τ(M)).

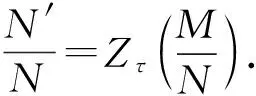
类似还可以定义N″,N‴,…等.易知N′,N″,…可以表示为

N′={m∈M|(N:m)≤τ-eR},N″={m∈M|(N′:m)≤τ-eR},…….

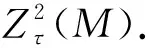
引理1[10]设M是模,N≤M.若M是τ-非奇异模,则以下成立:

(1)N≤τ-eN′;

(3)N′是M的包含N的最小τ-闭子模;(特别地,N′是N的τ-闭包)

(4)N″=N′;

(5)N=N′当且仅当N是M的τ-闭子模;

(6) 若Ni(i∈I)是M的τ-闭子模,则∩INi是M的τ-闭子模.

定义1[13]称M是τ-C11模,如果M满足下列等价条件之一:

(1)对任意N≤τ-dM,存在M的直和项K,使得K是N在M中的τ-补;

(2)对任意N≤τ-dM,存在M的直和项K,使得K∩N=0,且K⊕N≤τ-eM.

由文献[12，13],如下递推关系成立:

M是τ-C1模⟹M是τ-C11模⟹M是τ-FI-extending模.

1 主要结论

下面结论说明τ-C11模的有限直和仍是τ-C11模.

命题1 设M=M1⊕M2,若M1和M2是τ-C11模,则M是τ-C11模.

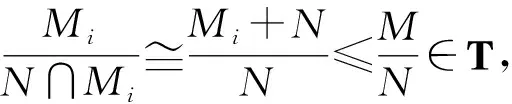
由命题1易得如下结论.

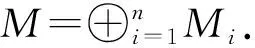
命题2 设M=M1⊕M2,其中M1◁τ-dM.则M是τ-C11模当且仅当M1和M2是τ-C11模.

证明必要性.先证M1是τ-C11模.设N1≤τ-dM1,则N1≤τ-dM.故存在M的直和项K,使得N1∩K=0,N1⊕K≤τ-eM.且存在L≤M,使得M=L⊕K.易知,M1∩K是M1的直和项.又

且N1⊕(M1∩K)=M1∩(N1⊕K)≤eM1,故N1⊕(M1∩K)≤τ-eM1.从而M1是τ-C11模.

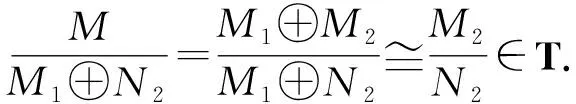
充分性.由命题1得证.

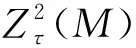
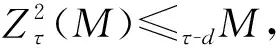
下面给出τ-C11模的一个等价刻画.

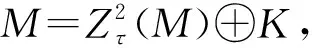
证明充分性.由命题2和命题3得证.

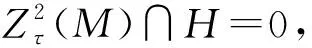
定理2 设M是模,N◁τ-dM.若M是τ-C11模,则存在M1,M2≤M,使得M=M1⊕M2,其中N≤τ-eM1.进而,以下结论成立:

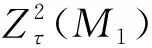
(3) 若M1◁M,则M1和M2是τ-C11模;

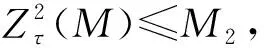
证明因为M是τ-C11模,所以M是τ-FI-extending模,故存在M1和M2,使得N≤τ-eM1,M=M1⊕M2.

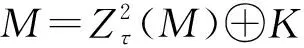
由命题2的证明过程知,Ki(i=1,2)是τ-C11模.从而由定理1知，(1)和(2)成立.

(3) 由命题2易证.