Gorenstein FPn-内射模和Gorenstein FPn-平坦模
陈 东, 胡 葵
(1. 成都大学 信息科学与工程学院, 四川 成都 610106; 2. 西南科技大学 理学院, 四川 绵阳 621010)
1 引言及预备知识
Gorenstein内射模和Gorenstein平坦模是Gorenstein同调理论中的基本研究对象,文献[1-3]用FP-内射模代替内射模,引入了GorensteinFP-内射模和Ding内射模的概念.称R-模M是GorensteinFP-内射模,如果存在FP-内射模Ii和Ii的正合列
…→I1→I0→I0→I1→…,
使得M≅ker(I0→I0),且对任意的FP-内射模I,函子HomR(I,-)使上述正合列保持正合.称R-模M是Ding内射模,如果存在内射模Ei和Ei的正合列
…→E1→E0→E0→E1→…,
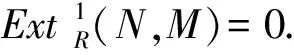
Fn→Fn-1→…→F1→F0→N→0,
其中每个Fi是有限生成的自由模或投射模.容易看到,当R是Noether环时,FPn-内射模和内射模是一致的.相关概念参见文献[4],不再赘述.
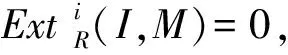
为讨论方便,本文恒设R是交换环,所讨论的环均指有单位元的结合环,模指酉模.用FIn表示FPn-内射模,⊥M表示M的左正交补,M+表示M的特征模HomZ(M,Q/Z).
2 主要结果
定义 11) 称R-模M是GorensteinFPn-内射模,如果存在FPn-内射模Ei和Ei的正合列
…→E1→E0→E0→E1→…,
(1)
使得M≅ker(E0→E0),且对任意的FPn-内射模I,函子HomR(I,-)使上述正合列保持正合.2) 称R-模M是GorensteinFPn-平坦模,如果存在FPn-平坦模Fi和Fi的正合列
…→F1→F0→F0→F1→…,
(2)
使得M≅ker(F0→F0),且对任意的FPn-内射模I,函子I⊗-使上述正合列保持正合.
定义 21) 称R-模M是n-Ding内射模,如果存在内射模Ei和Ei的正合列
…→E1→E0→E0→E1→…,
使得M≅ker(E0→E0),且对任意的FPn-内射模I,函子HomR(I,-)使上述正合列保持正合.2) 称R-模M是n-Ding平坦模,如果存在平坦模Fi和Fi的正合列
…→F1→F0→F0→F1→…,
使得M≅ker(F0→F0),且对任意的FPn-内射模I,函子I⊗-使上述正合列保持正合.
注 3由定义:
1) {内射模}⊆{FP-内射模}⊆{FPn-内射模}⊆{GorensteinFPn-内射模};
{平坦模}⊆{FPn-平坦模}⊆{GorensteinFPn-平坦模}.
2) GorensteinFP0-内射模是Gorenstein内射模,GorensteinFP1-内射模是GorensteinFP-内射模;GorensteinFP0-平坦模和GorensteinFP1-平坦模恰好是Gorenstein平坦模.
3) {n-Ding内射模}⊆{Gorenstein内射模},{n-Ding平坦模}⊆{Gorenstein平坦模}.
4) 正合列(1)和(2)中所有的像、核、上核都是GorensteinFPn-内射模(或GorensteinFPn-平坦模).
5) GorensteinFPn-内射模对直积、直和加项封闭;GorensteinFPn-平坦模对直和、直和加项封闭.
命题 4设M是GorensteinFPn-平坦模,则M+是GorensteinFPn-内射模.
证明由于M是GorensteinFPn-平坦模,故存在FPn-平坦模Fi和Fi的正合列
F=…→F1→F0→F0→F1→…,
使得M≅ker(F0→F0),且对任意的FPn-内射模E,E⊗F是正合的.于是又有
(E⊗F)+=…→(E⊗F1)+→(E⊗F0)+→
(E⊗F0)+→(E⊗F1)+→…
(3)
是正合的.由于(Fi)+和(Fi)+是FPn-内射模,从而有
F+=…→(F1)+→(F0)+→
(F0)+→(F1)+→…
是FPn-内射模的正合列,且M+≅ker((F0)+→(F0)+).另一方面,对正合列(3),由相伴同构定理知
…→HomR(E,(F1)+)→HomR(E,(F0)+)→
HomR(E,(F0)+)→HomR(E,(F1)+)→…
是正合的.因此,M+是GorensteinFPn-内射模.
文献[7]中定义了R-模M的FP-内射维数

其中N是有限表现模}.
相应地,可以定义R-模M的FPn-内射维数

其中N是n-有限表现模}.
以下给出n-凝聚环上FPn-内射维数的一个刻画:
命题 5设R是n-凝聚环,则M的FPn-内射维数FPn-idR(M)≤n,当且仅当存在正合列
0→M→E0→E1→…→En→0,
其中每个Ei是FPn-内射模.

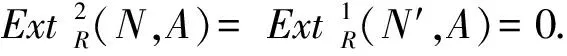
命题 6设R是n-凝聚环,M是GorensteinFPn-内射模,则M的FPn-内射维数FPn-idR(M)等于0或∞.
证明设FPn-idR(M)=n<∞,由命题5,存在FPn-内射模的正合列
0→M→E0→E1→…→En→0.
从而又有短正合列:
0→M→E0→C0→0,
0→C0→E1→C1→0,
……
0→Cn-2→En-1→En→0,
由于M是GorensteinFPn-内射模,故对任意的FPn-内射模I,函子HomR(I,-)使上述所有正合列保持正合.因而有正合列
HomR(En,En-1)→HomR(En,En)→0.
于是该正合列分裂,故Cn-2是FPn-内射模.类似的方法如此下去,得到每个Ci都是FPn-内射模.由第一个短正合列,M是FPn-内射模.
文献[1]证明了环R是Noether环当且仅当每个FP-内射模是Gorenstein内射模,当且仅当每个GorensteinFP-内射模是Gorenstein内射模.现用GorensteinFPn-内射模刻画Noether环.
定理 7以下各条等价:
1)R是Noether环;
2) 每个FPn-内射模是Gorenstein内射模;
3) 每个FPn-内射模是n-Ding内射模;
4) 每个GorensteinFPn-内射模是Gorenstein内射模;
5) 每个GorensteinFPn-内射模是n-Ding内射模.
证明1)⟹3)⟹2),1)⟹4)⟹2)和1)⟹5)⟹3)显然.
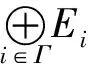

于是又有正合列
即
近年来,许多学者研究了Gorenstein同调模的结构.2010年,文献[8]证明了若R是Gorenstein环且Krull维数有限,则每个Gorenstein内射模也可以分解为不可分解的Gorenstein内射模的直和.2018年,文献[6]证明了一个局部2-强Gorenstein半单环R上每个R-模M都有分解M=R(I)⊕N,其中R(I)是秩为I的自由模,N满足对任意x∈N,都有Ann(x)≠0,其中Ann(x)表示元素x的零化子.现讨论n-凝聚环上GorensteinFPn-内射模的结构.

定理 8设R是n-凝聚环,M是GorensteinFPn-内射模,则有M≅F⊕H,其中F是FPn-内射模,H是FIn-内射模.
证明由于M是GorensteinFPn-内射模,故存在M的全FPn-内射分解
…→E1→E0→E0→E1→…,
使得M≅ker(E0→E0),且函子HomR(FIn,-)使上述正合列保持正合.取K=cok(M→E0),由于R是n-凝聚环,故由文献[10],K有FPn-内射盖g:G0→K,取M0=ker(G0→K).容易验证g是满射.由于M是GorensteinFPn-内射模,故对FPn-内射模G0,有正合列
HomR(G0,E0)→HomR(G0,K)→0.
于是存在以下行为正合列的交换图:
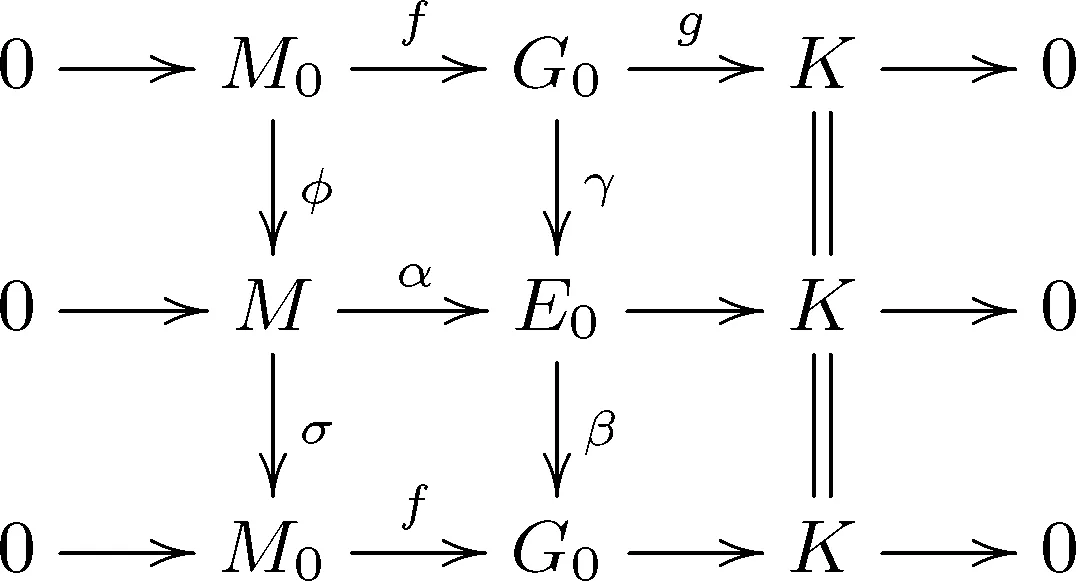
注意到βγ是同构,故E0=ker(β)⊕Im(γ),因而Im(γ)≅G0且ker(β)是FPn-内射模.另一方面,M0是FIn-内射模.由于σφ是同构,由引理5有M=ker(σ)⊕Im(φ),其中Im(φ)≅M0.考虑以下交换图:

因而有ker(σ)=ker(β).
由于1-凝聚环是凝聚环,容易得到以下结论.
推论 9[1]设R是凝聚环,M是GorensteinFP-内射模,则M≅F⊕H,其中F是FP-内射模,H是FI-内射模.
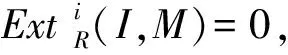
证明设f0:E0→M是M的FPn-内射盖,由于R是自FPn-内射的,因此f0是满射.于是存在正合列
且对任意的FPn-内射模I,
HomR(I,E0)→HomR(I,M)→0
是正合的.对K0,又存在f1:E1→K0是K0的FPn-内射盖,由于R是自FPn-内射的,因此f1也是满射.于是又存在正合列
且对任意的FPn-内射模I,
HomR(I,E1)→HomR(I,K0)→0
是正合的.如此下去,可以构造M的左FPn-内射分解
…→E1→E0→M→0,
且对任意的FPn-内射模I,函子HomR(I,-)使上述正合列保持正合.
另一方面,取M的右内射分解
0→M→E0→E1→…,

综上,存在M的全FPn-内射分解
…→E1→E0→E0→E1→…,
使得M≅ker(E0→E0),且对任意的FPn-内射模I,函子HomR(I,-)使上述正合列保持正合.
推论 11[11]设R是QF环,则每个R-模M是Gorenstein内射模.
环R称为n-FC环,若R是凝聚环,且R的自FP-内射维数小于等于n(FP-idRR≤n).特别地,0-FC环称为FC环,FC环也是IF环.
推论 12[1]设R是完全的FC环,则每个R-模M是GorensteinFP-内射模.
致谢成都大学青年基金(2018XZA08)对本文给予了资助,谨致谢意.

