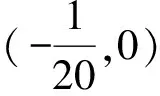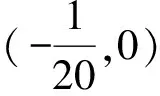一类Abel积分的零点个数估计
王喜红
(宁夏师范学院 数学与计算机科学学院, 宁夏 固原 756000)
1 引言和主要结果
考虑超椭圆Hamilton系统
其中,P(x)∈R[x],degP(x)=5.不失一般性,假设最高次项的系数为正,与H(x,y)相应的Hamilton系统有4个奇点(0,0)、(μ,0)、(λ,0)和(1,0),其中0≤μ≤λ≤1.Gavrilov等[1]给出H(x,y)的规范型为
(1)
与其相对应的Hamilton系统为

(2)
文献[1]考虑了如下形式的Abel积分
的零点个数问题,其中
Γh⊂{(x,y)∈R2|H(x,y)=h}.
2013年,Wang等[2]研究了当Γh是文献[1]中退化卵形线时,Abel积分(2)的零点个数问题,并证明了此类Abel积分恰好有一个零点.
当λ=μ=0时,系统(1)变为
(3)
与其相应的Hamilton函数为
(4)

α0J0(h)+α1J1(h)+α2J2(h)+α3J3(h),
其中

图 1 系统(3)的相图
本文的主要结果如下.




2 预备知识
首先介绍一些本文用到的概念和结论,更详细的结果见文献[3-4].
定义 2.1设f0,f1,…,fn-1是开区间I⊂R上的解析函数.
1) {f0,f1,…,fn-1}是I上的Chebyshev系统(简称T-系统)当且仅当任何非平凡的实线性组合α0f0(x)+α1f1(x)+…+αn-1fn-1在I上至多有n-1个孤立零点.
2) 如果{f0,f1,…,fk-1}是I上的Chebyshev系统,k=1,2,…,n,则{f0,f1,…,fn-1}是I上的完全的Chebyshev系统(简称CT-系统).
3) 如果对每个k=1,2,…,n,任何非平凡的线性组合α0f0(x)+α1f1(x)+…+αk-1fk-1在I上至多有k-1个孤立零点(计重数),则{f0,f1,…,fn-1}是I上的扩展的完全的Chebyshev系统(简称ECT-系统).
4) 如果任何非平凡的线性组合α0f0(x)+α1f1(x)+…+αn-1fn-1在I上至多有n+m-1个孤立零点,则{f0,f1,…,fn-1}是I上具有精度m的Chebyshev系统.
注 2.1根据文献[5-6]中结果,如果{f0(x),f1(x),…,fn-1(x)}是I上的ECT-系统,则对每个k=1,2,…,n-1,存在{f0,f1,…,fn-1}的一个实线性组合在I上恰好有k个孤立零点.如果{f0(x),f1(x),…,fn-1(x)}是I上精度为m的T-系统,则存在{f0,f1,…,fn-1}的实线性组合在I上至多有n+m-1个孤立零点.
引理 2.1{f0,f1,…,fn-1}是I上的ECT-系统当且仅当对每个k=1,2,…,n和所有的 x∈I,Wronsky行列式W[f0,f1,…,fk-1](x)≠0.
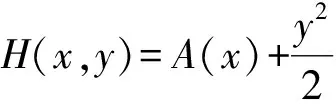
Γh⊂{(x,y)|H(x,y)=h,
h0 P在x轴上的投影是区间(xl,xr),且xl<0 A(x)=A(z(x)),x∈(0,xr). 考虑Abel积分 h∈(h0,0)或h∈(0,h1), 其中gi(i=0,1,…,n-1)是区间(xl,xr)上的解析函数,s∈N.定义区间(0,xr)上的解析函数 (5) 则由引理2.1可得下面的代数准则(见文献[3]中定理B和文献[4]中定理A). 引理 2.21) 如果s>n-2,对每个i=0,1,…,n-1和x∈(0,xr),W[l0,l1,…,li]≠0,则{I0(h),I1(h),…,In-1(h)}是区间(h0,0)或(0,h1)上的ECT-系统. 2) 如果s>n+m-2,对每个i=0,1,…,n-2和x∈(0,xr),W[l0,l1,…,li]≠0,且W[l0,l1,…,ln-1]在(0,xr)上有m个零点(计重数),则{I0(h),I1(h),…,In-1(h)}在(0,xl)上至多有n+m-1个孤立零点(计重数). 其中 令x=1-u,y=-v,把系统(3)的中心C(1,0)移到原点(仍记为( x,y)).系统(3)变为 (6) 与它对应的 Hamilton 函数是 它在原点取局部最小值,且卵形线γl围绕原点(0,0),其中 q(x,z)=4x4-15x3+4zx3+20x2-14zx2+ 4z2x2-10x+20zx-15z2x+ 4xz3-10z+20z2-15z3+4z4, 进而可得 30zx+8z2x-10+20z-15z2+4z3]/ [4x3-15x2+8zx2+20x-30zx+ 12z2x-10+40z-45z2+16z3]≜Θ. (7) 对系统(6),定义 其中 因为n=3,s=1,引理2.2中的s>n-2仍不满足,需要再次提高y的幂.再由引理2.3可得 其中 (8) 定义 计算可得 φi(x,z)=η1(x,z)mi(x,z), 其中 mi(x,z)是(x,z)的多项式.由引理2.2,只需证明对任意的x∈(0,1)有 W[m1]≠0,W[m1,m2]≠0, W[m1,m2,m3]≠0. 事实上,令 其中 Θ由(7)式定义.计算可得 W[m1]=m1(x,z), 其中z=z(x)满足q(x,z)=0,σi(x,z)(i=1,2)是(x,z)的多项式,有 ξ(x,z)=4x3-15x2+8zx2+20x-30zx+ 12z2x-10+40z-45z2+16z3. (9) 下面用Maple计算2个多项式之间的结式,并应用斯图姆定理证明这2个多项式没有公共零点. q(x,z)和m1(x,z)关于z的结式是(x-1)42ζ0(x),其中ζ0(x)是x的62次多项式.由斯图姆定理可得ζ0(x)≠0,x∈(0,1).因此,W[m1]≠0,x∈(0,1).q(x,z)和ξ(x,z)关于z的结式是 R(q,ξ,z)=8 000(4x+1)3(x-1)6× (4x3-15x2+20x-10). 类似于引理3.1的证明可得如下引理3.2. 引理 3.3当0<-h≪1时,Jk(h)(k=0,1,2,3)有下列展式: 其中r1>0和r2<0是常数. 证明因为 (10) 其中 首先计算Ii(h)在x=0处的展式.由文献[7]可得 I(h)=α0I0(h)+α1I1(h)+α2I2(h)+α3I3(h)= 其中 如果c2=c3=0,计算可得 其中r1>0和r2<0是常数.注意到 I(h)=α0I0(h)+α1I1(h)+α2I2(h)+α3I3(h) 和(10)式,即可得结论成立.证毕. 证明令x=u+1,y=v,则系统(11)变为 α2(u+1)2+α3(u+1)3)v. (12) 令u=rcosθ,v=rsinθ,则当0 化为 令 F(r,ρ)= 对F(r,ρ)在(r,ρ)=(0,0)处应用隐函数定理,存在一个光滑函数r=φ(ρ)和常数δ,0<δ≪1,使得当0<ρ<δ时,F(φ(ρ),ρ)≡0.计算可得 (13) 注意到 α3(u+1)3)vdu. 由(13)式可得 α3(u+1)3)vdu= α3(u+1)3)dudv= α2(rcosθ+1)2+α3(rcosθ+1)3)rdr. (14) I(l)=c1l+c2l2+c3l3+c4l4+O(l5), (15) 其中 c1=2π(α0+α1+α2+α3), 24 606 689α2-10 431 649α3). 因为 I(h)=α0I0(h)+α1I1(h)+ α2I2(h)+α3I3(h), 再注意到(10)式,即可得结论成立.证毕. 证明直接计算可得 由引理3.3和引理3.4可得 P2(0-)=0,P3(0-)=0, α0J0+αiJi=J0(α0+αiPi(h)),i=2,3, 证明当α3=0时,有 J(h)=α0J0(h)+α1J1(h)+α2J2(h)= J0(h)(α0+α1P1(h)+α2P2(h)). 所以J(h)的零点个数等于直线L:α0+α2P+α1P1=0与曲线Σ1的交点个数.直接计算可得 再由引理3.3和引理3.4可得 1 599.565 8>0. 时,L和Σ1至少有5个交点(计重数),进而可得 类似于定理3.1的证明,可得下面定理.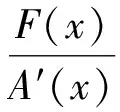
3 定理1.1的证明