磁性杂质在铁基超导体中引起的隙内束缚态

刘江山, 马建明, 刘志海, 郑铁军, 张德刚

(1. 四川师范大学 物理与电子工程学院, 四川 成都 610101；2. 中山大学 物理学院， 广东 广州 510275；3. 成都纺织高等专科学校 基础部， 四川 成都 611731)

自2008年新型超导材料铁基超导体发现以来[1-5],铁基高温超导体的超导电性一直都是凝聚态物理所研究的热门课题之一，其中杂质是研究超导序参量的对称性的一种基本手段[6].对于不同的超导序参量，在能隙内的局域态密度(LODS)有不同的特征.不同于非磁性杂质，磁性杂质在任何序参量下均产生2个(多个)杂质共振峰，与自旋上、下相联系.随着强度增加，两峰交错移动，呈周期性变化.在铁基超导体中，LODS主要显示较强磁性或非磁性杂质势的特征.在超导体中磁性杂质会破坏时间反演对称性，并在超导能隙中诱导出束缚态[7-8].目前为止，超导材料中获得的最高转变温度( TC)高达55 K[2],类似于铜氧超导体.铁基超导体也有一个层状结构，它的超导电性来自Fe-Fe平面内传导电子配对——电子库珀对.在铁基超导体两轨道四带紧束缚模型[9]中,每个原胞中包括2类原子Fe(A和B)和As(A和B).有2个配体As(Se)原子分别位于铁平面面心的上方和下方，4个As原子构成四面体，而铁原子位于四面体的体心.角分辨光电子能谱(ARPES)实验[10-14]和能带计算[15-16]已经得出费米面[14,17]是由围绕在布里渊区 Γ (0,0)点的2个空穴型费米面( α,β)和围绕在 M (π,π)点的2个电子型费米面(γ,δ)构成.

对于没有能隙节点的s波超导体，磁性杂质和非磁性杂质对库珀对的影响不同.对于s+-超导体，非磁性杂质散射是一种拆对作用，对于s++超导体，磁性杂质有拆对作用[18].通过STM实验[19-20]描述铁基超导体中杂质点及其近邻点的局域态密度,可以直接观察磁性杂质引起的隙内束缚态[21-23].而非磁性杂质散射会在S±-波配对对称性中引起隙内束缚态[24]，该类束缚态不会出现在s-波配对对称性中[9,25-26].单个磁性杂质[27-28]对局域态密度的影响，在磁性杂质势下，存在零能共振峰，超导相干峰也受到抑制，并且在杂质势的变化过程中，共振峰会发生劈裂.随着磁性势的增强，零能处附近的共振峰强度逐渐变弱，同时导致劈裂发生.

本文基于两轨道四带模型的两轨道和Raghu模型[29]相同，是由 dxz和 dyz轨道构成，但该模型认为铁基超导体表面层上、下方的2个砷原子是不对称分布的，对该平面内的电子态是有影响的.两轨道四带模型不仅能正确解释 Γ 点的2条空穴型带是非简并的，同时也符合ARPES实验[10,13]结果,而其他模型不能解释.该模型还成功解释非磁性杂质在超导能隙内产生的共振峰[30]和STM实验所观察到的涡流中的负能共振峰[1,31]、畴壁现象，同时，对于核磁共振和中子散射实验观测到的超导相图[32]、畴壁结构[33]都有完美的诠释.基于该理论模型，通过调节磁性势和非磁性势的大小，研究铁基超导体中单个磁性杂质诱导的超导能隙束缚态.

1 理论模型

本文考虑一个铁基超导体两轨道四带紧束缚模型[9]的两轨道是由 dxz和dyz简并轨道构成，并且与Raghu模型[29]相同.与铜氧超导体中位于Cu-Cu平面内的氧原子不同,在铁基超导体两轨道四带紧束缚模型中,每个原胞中包括2类原子Fe(A和B)和As(A和B)，有2个配体As原子A和B原子分别位于铁平面面心的上方和下方，4个As原子组成四面体，但该模型认为Fe-Fe 平面上、下方的2个砷原子是不对称分布的，而铁原子位于四面体的体中心,则两轨道四能带紧束缚模型的哈密顿量：

cBα,ij+1σ+cBα,i+1j+1σ)+

(1)

运用公式

作傅里叶变换，把实空间的哈密顿量转换到动量空间

(2)

进一步计算简化

2t4(coskx+cosky)×

[t1(1+ei kx+ei ky+ei (kx+ky))×

(3)

这里令

A,k=-2(t2coskx+t3cosky),

(4)

再次简化得

(5)

将H0写成矩阵形式，可得到该模型的本征方程

(6)

由于本征波函数不为零，则得到能量方程

(7)

并解出本征函数

(8)

进一步计算简化，令

作正则变换得

(9)

对H0最终对角化

(10)

为了研究超导电性，引入超导BCS理论的哈密顿量

(11)

由于磁性杂质项的哈密顿量Himp项

(12)

其中,Vm表示磁性势， Vs表示非磁性势.因此该两轨道四带模型系统总的哈密顿量

H=H0+HBCS+Himp.

(13)

采用波戈留波夫变换

(14)

最后对系统总的哈密顿量H进行对角化

(15)

现构造格林函数,使用格林函数的方法计算，则由格林函数得到

Gu′v,k′γ′uv,kγ(τ)=-〈Tτφuv,kγ(τ)φu′v′,k′γ′(0)〉, (16)

其中Tτ为时序算符

φuv,kγ(τ)=eHτφuv,kγe-Hτ,

(17)

经过计算，得出函数解

(18)

进一步计算

(19)

其中，经定义

(20)

解以上式子可得

α(iωn)=

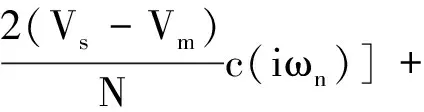
(21)

(22)

最后解得两轨道四带模型中磁性杂质的局域态密度公式

(23)

两轨道四带紧束缚模型中A、B格点总局域态密度分为自旋向上和自旋向下两部分,其中(23)式表示自旋向上时的局域态密度，继续计算,最终得出自旋向下的局域态密度公式

(-1)γ+1ξuv,kγ+1ξuv,kγ×

(-1)γ′+1ξu′v,k′γ′ξu′v,k′γ′+1-

(-1)γ′+1ξu′v,k′γ′ξu′v,k′γ′+1+

(24)

以上公式中有

a(-iwn)=-c(iwn),

c(-iwn)=-a(iwn),

b(-iwn)=b(iwn),

在下面的计算中，将采用文献[21]中的相关参数:

Δ0=5.8 meV,t1=0.5,t2=0.2,t3=-1.0,t4=0.02,μ=-0.49 eV,

并且在理想电子掺杂情况(15%).

2 磁性杂质引起的隙内束缚态

由(23)和(24)式计算得到无杂质时(Vs=0 eV,Vm=0 eV ) ,杂质点附近周围晶格A和晶格B原点处的局域态密度图像.图1(a)中能够清晰地观察到在无杂质时，晶格A原子和晶格B原子原点处的局域态密度曲线基本重合，而次近邻Fe和最近邻Fe原子处的局域态密度曲线也基本重合.这是因为铁基超导体的结构为多费米面结构.在正负能侧，明显地存在2个共振峰，并且有2个大小不同的能隙，分别为Δ=0.005 8 eV和Δ2=0.004 8 eV，其中较小能隙与β费米面有关[5,34].计算结果符合STM实验[22]观测到的结果.

下面将计算单个磁性杂质在晶格A原子原点处对局域态密度的影响.如图1(b)当|Vm|较小时，|Vm|磁性势对局域态密度影响较小，可以忽略不计.当|Vm|磁性势较强时，总是表现出破坏库珀对行为，Δuv,k杂质点附近的局域态密度与|Δuv,k|有相似的共振峰结构,但Vm值与间隙共振峰的位置是不同的.根据以上计算并由数据分析得到结果，若非磁性势Vs取定值，在磁性势Vm处的局域态密度与|Vm|(Vm)处基本相同,如图2(b)和(c).

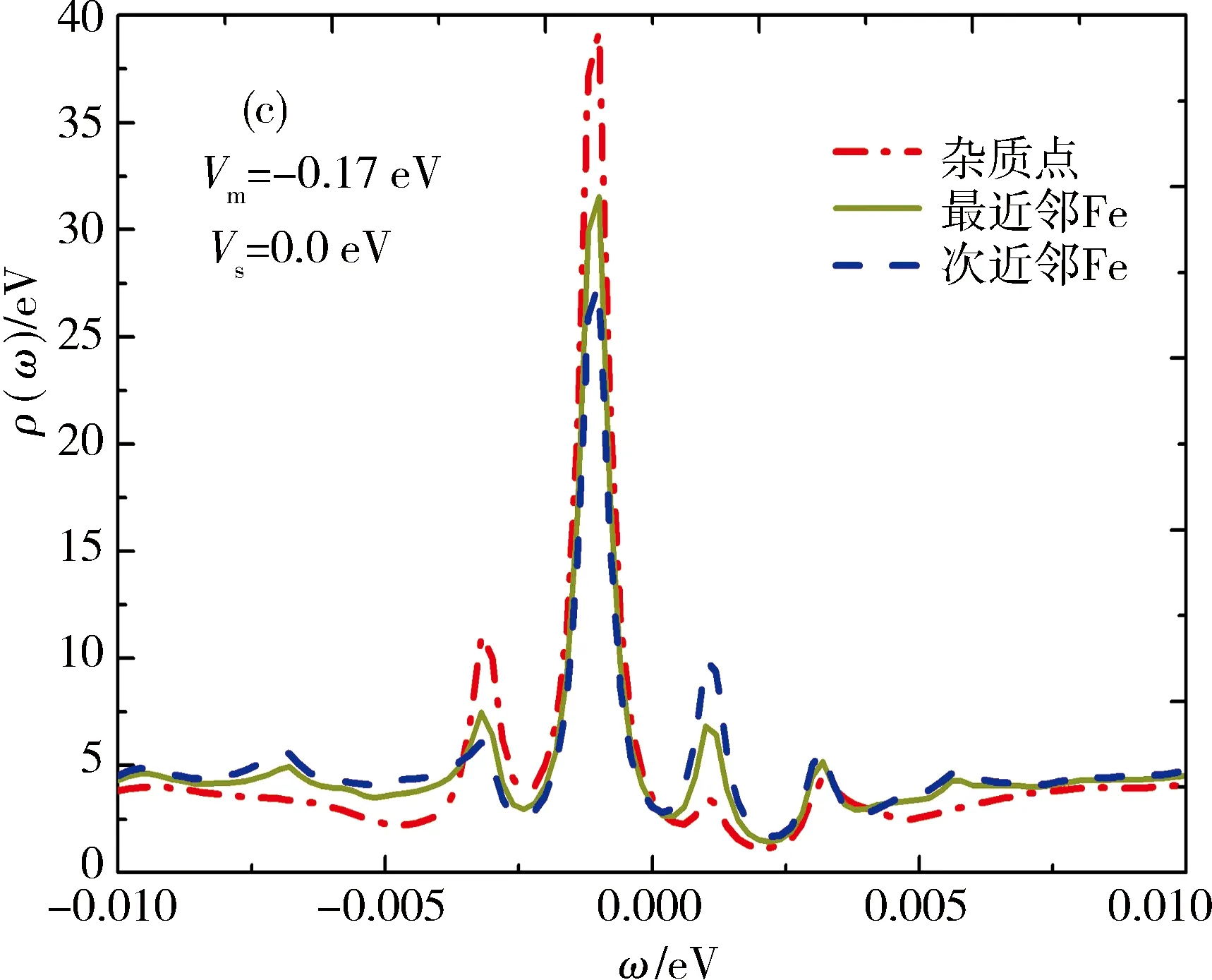
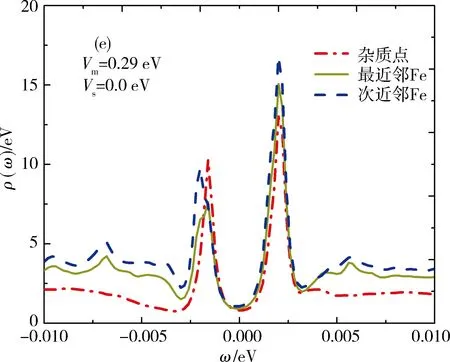
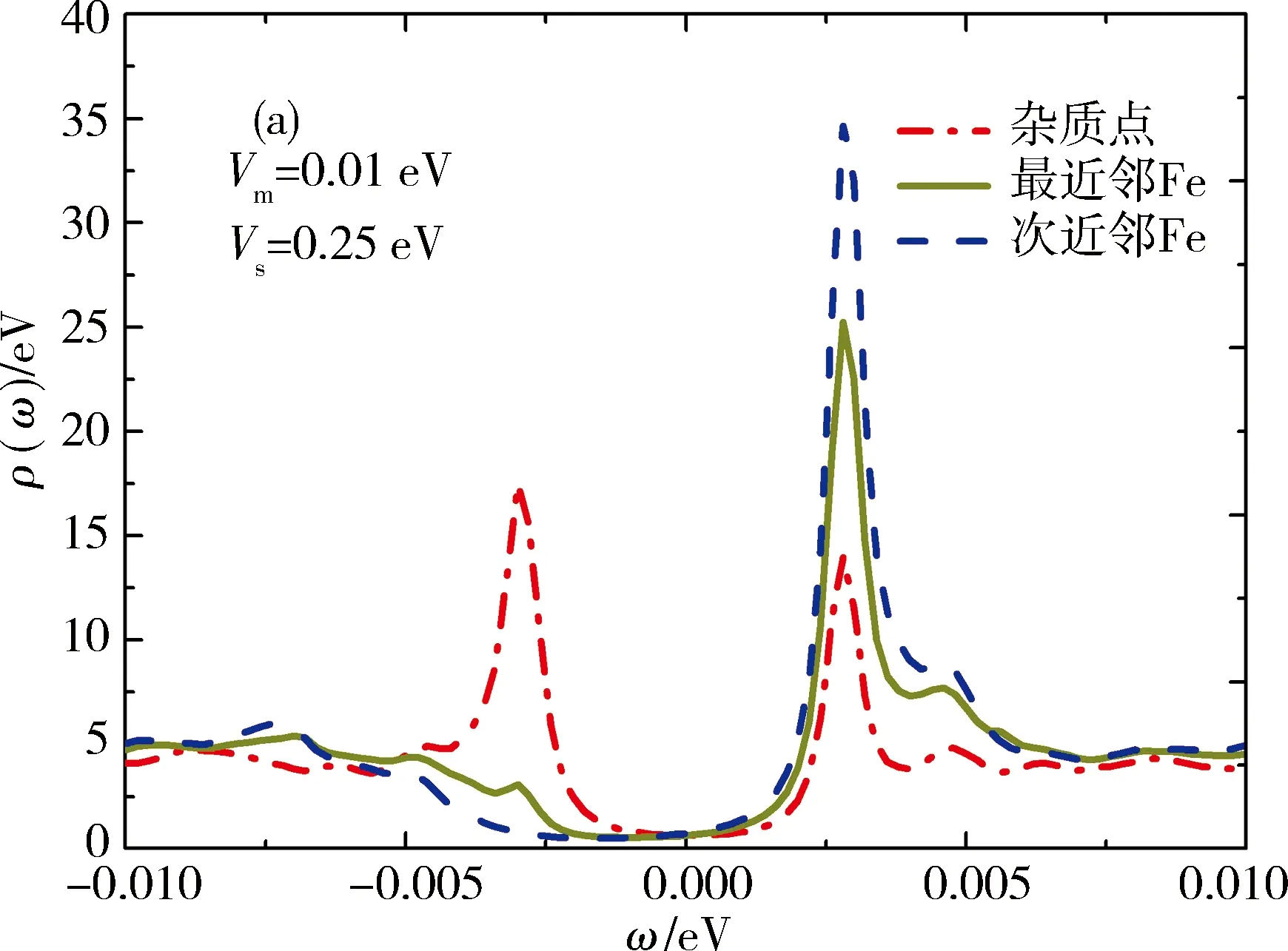
当Vs=0 eV，即混合势表现为磁性势，对于杂质点、最近邻点、次近邻点，分析得到当Vm=0.1 eV时，在正、负能侧相对应位置，可以观察到一大一小2个杂质共振峰，高度较大的共振峰出现在负能侧.当Vm=0.2 eV时，在零能位置(ω=0)处出现峰值较高共振峰，极小的峰值在ω=2.8 meV处.随着磁性势增大，出现多个峰，且正负能侧杂质共振峰高度变化趋势先增大后减小，并且能隙逐渐向零能位置移动.其中最近邻点，在Vm=0.29 eV时，负能侧局域态密度的共振峰发生劈裂,而杂质点和次近邻点的共振峰只在Vm>0.29 eV时才会发生劈裂.在次近邻点和最近邻点上，共振峰出现的位置相同，而次近邻点较大峰值始终高于最近邻点上.当Vm→+∞时,杂质点的局域态密度趋于零.

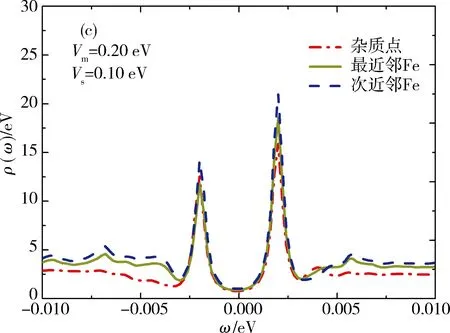
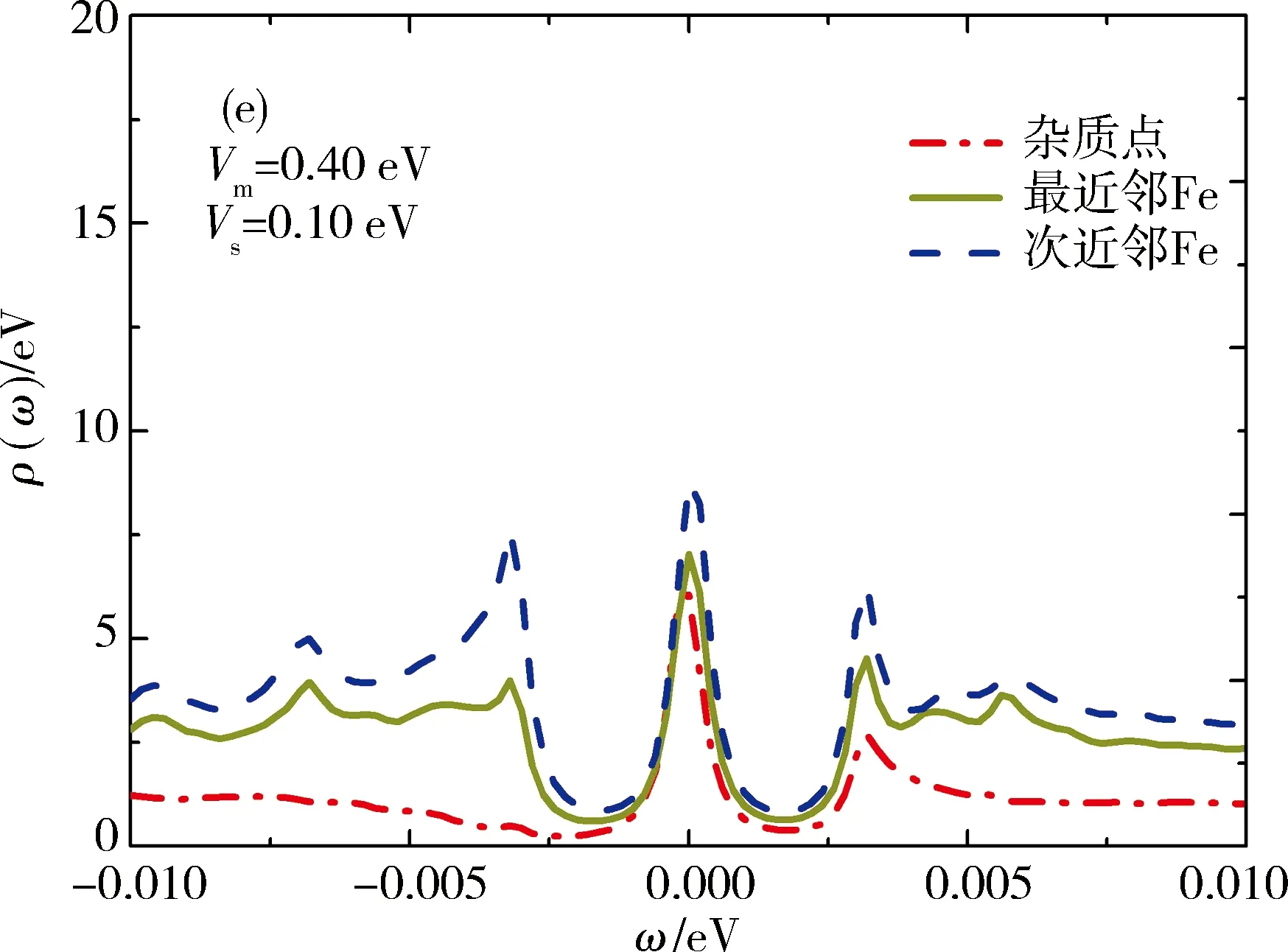
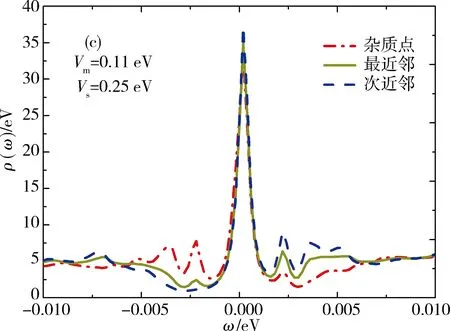
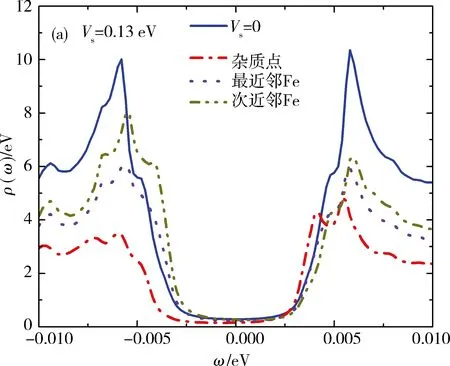
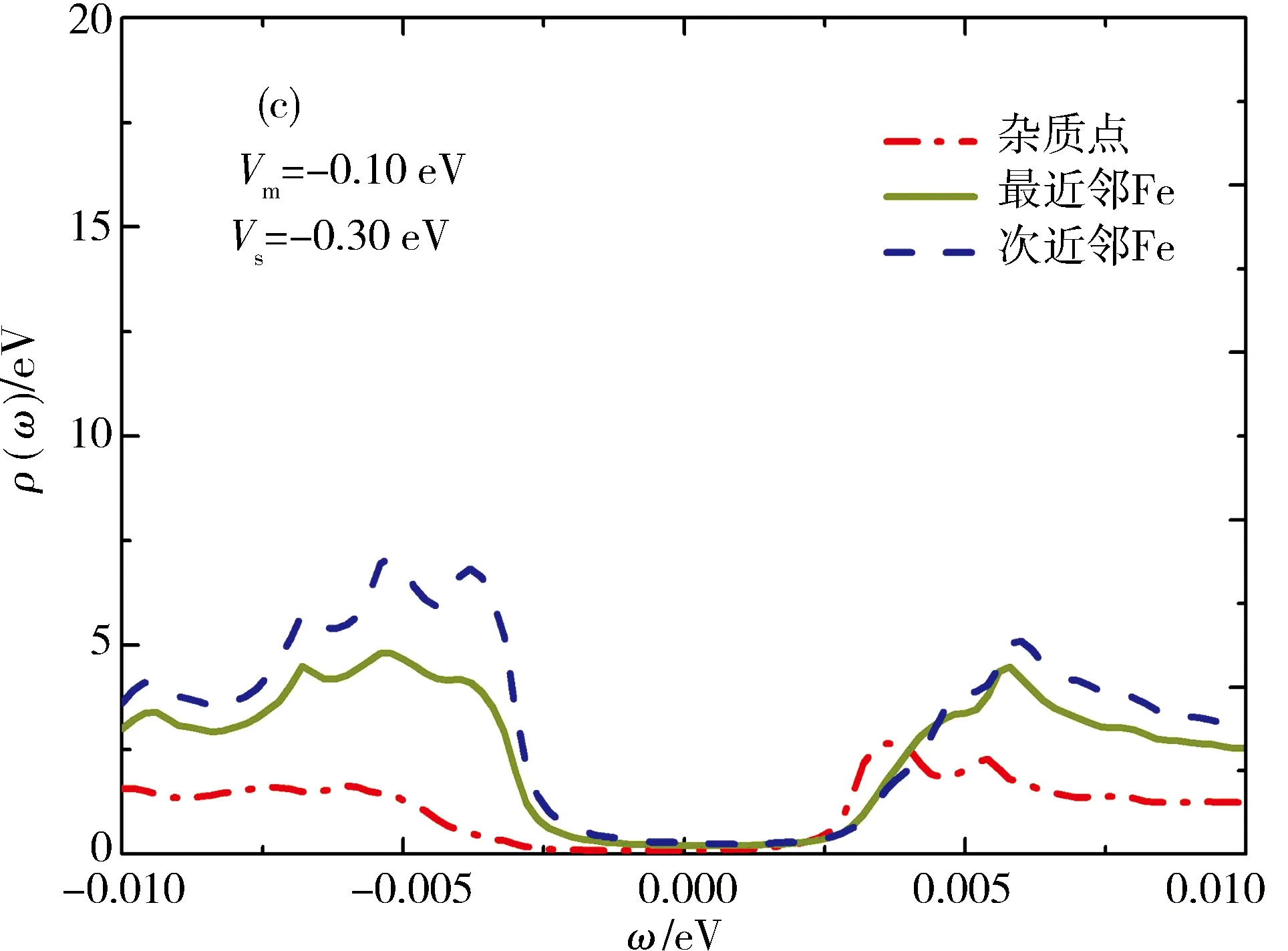
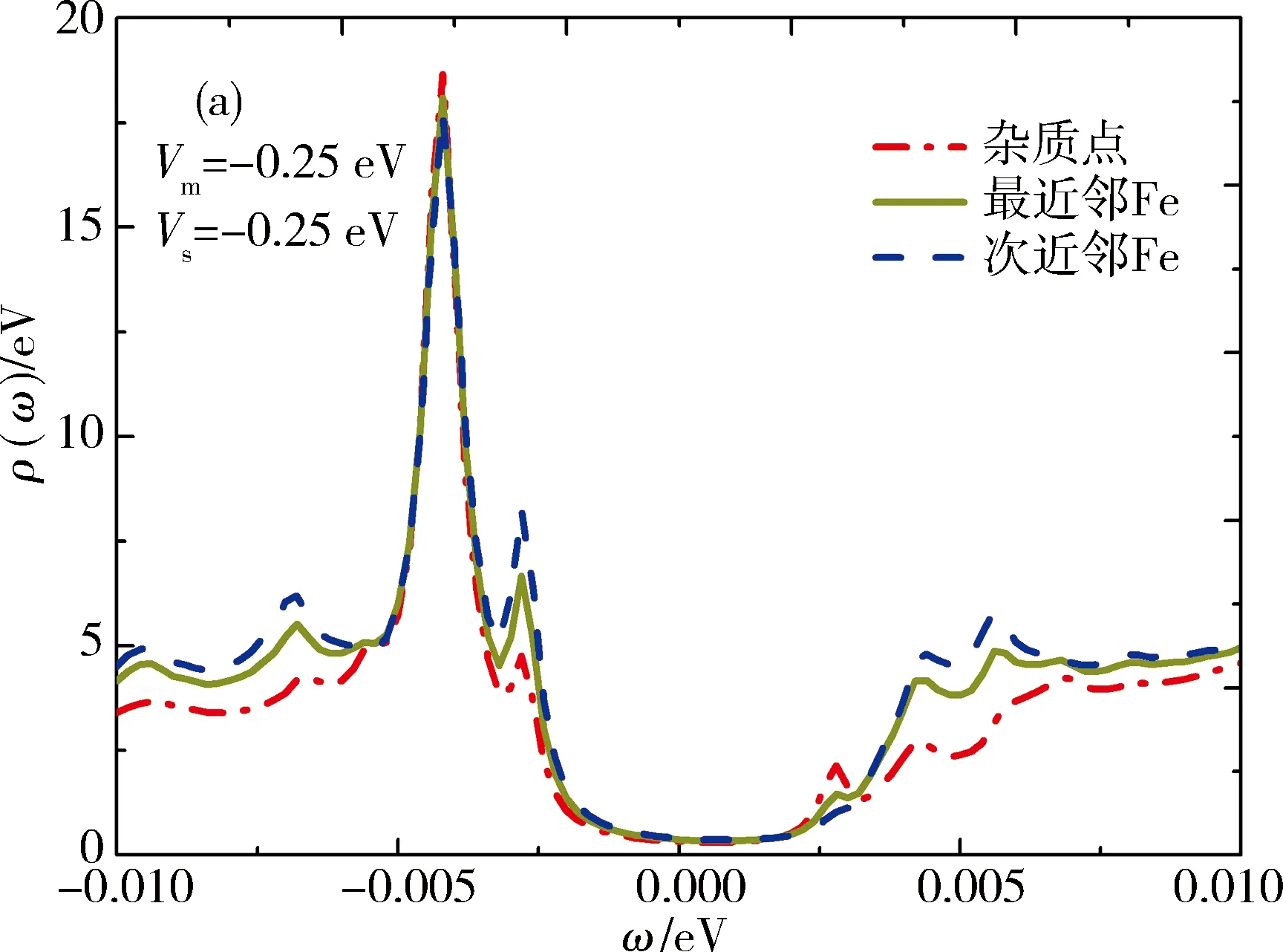
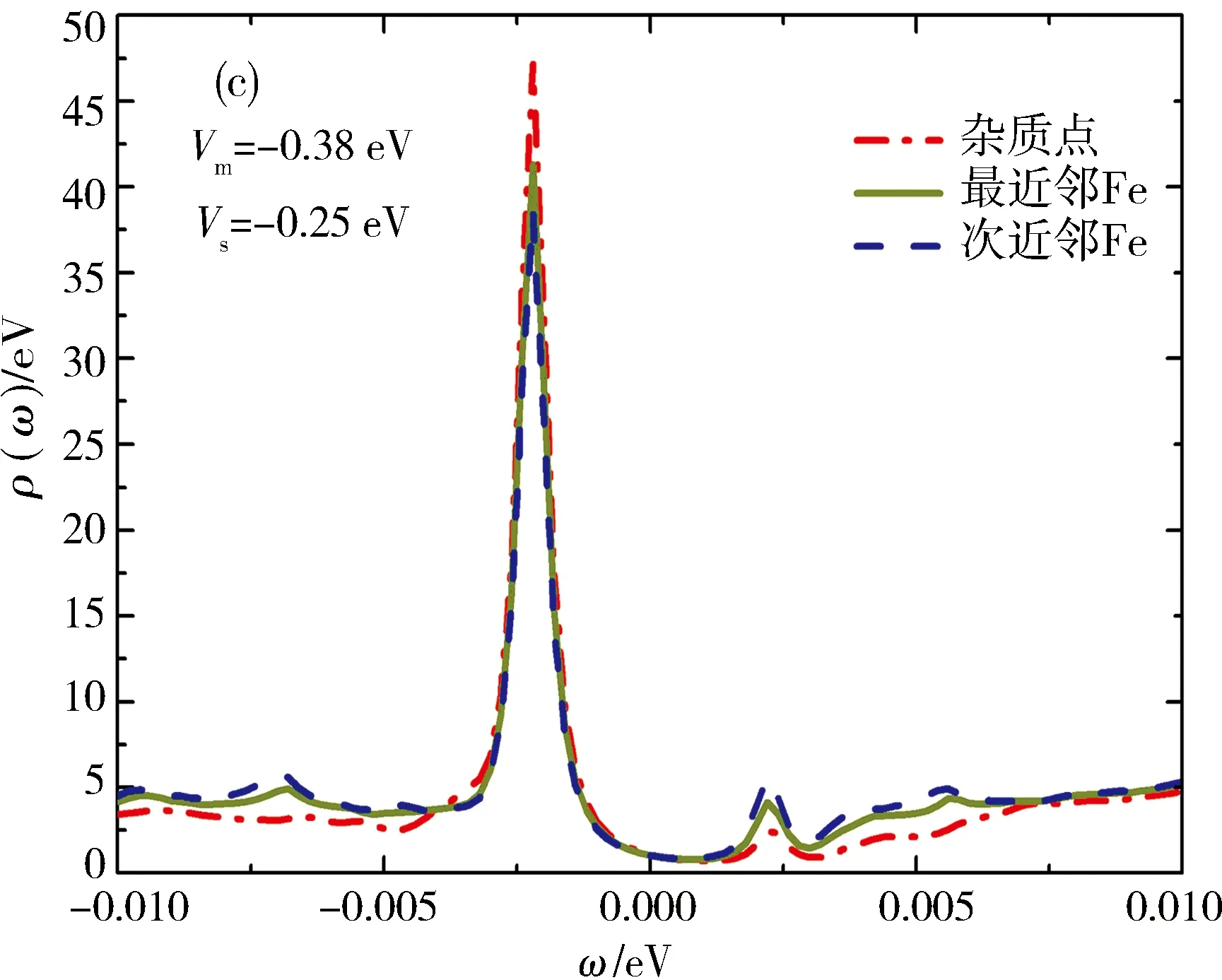
下面讨论磁性势(Vm)和非磁性势(Vs)同时存在时，杂质对局域态密度的影响.当磁性势大于非磁性势时，主要表现出磁性势，局域态密度则主要显磁性势的特征.图3描述的是杂质势(Vs>0,排斥势)在次近邻点、最近邻点及杂质点上取不同值时，对局域态密度的影响.Vs较小(Vs

图4表示当Vs>Vm时，杂质对局域态密度的影响.Vm=0时，对于次近邻点，在0.17～0.30 eV范围内，负能侧的共振峰消失，当Vs>0.30 eV时，共振峰又重新出现，并能够明显观察到.而对于最近邻点在0.36～1.0 eV范围内，在负能侧不能观察到清晰的共振峰，而且较高峰值的共振峰出现在正能侧方向.前面已提到过当磁性势较小，对局域态密度的影响极小.随着Vm增大，磁性势会抑制相干峰的强度.其中，取其非磁性势Vs=0.25 eV不变，磁性势增加，在0～0.05 eV范围内，杂质点上的局域态密度出现2个共振峰.在ω=-3.0 meV处存在单个共振峰，且在正能侧的峰向零能位置移动，其高度要低于负能侧，并逐渐变小，而负能侧的峰也向零能点移动.对于杂质点，当Vm>0.05 eV时，出现在负能侧的共振峰峰劈裂成多个峰，随着Vm继续增大，共振峰先逐渐消失后又出现，呈周期性变化.对于最近邻点和次近邻点，Vm<0.12 eV时,共振峰只出现正能侧，2个点的局域态密度的变化趋势基本相同.对于杂质点,当Vm→+时，局域态密度趋于零.发现3个点峰值最大的共振峰都出现在零能处.

当Vm>0.12 eV时，以上较大的共振峰经过零能位置，出现在负能侧.经过对数据分析,次近邻点上局域态密度峰值高度始终高于杂质点和最近邻点的局域态密度峰值.它们高度变化趋势先减小后增大再减小，最后变化趋势同上.

对于吸引势(Vs<0)，图5(a)[24]表示与Vs=0 eV的局域态密度相比，能够明显的观察到杂质共振峰高度更低，位置更加靠近能隙中心，而且对局域态密度的影响极小.随着|Vm|增大，能够在负能侧观察到不明显地的共振峰.当|Vm|<|Vs|时,杂质点、最近邻点、次近邻点局域态密度变化规律基本相同.

下面取非磁性势Vs=-0.25 eV时，通过计算和数据分析(如图6)，在|Vm|>|Vs|情况下，得出随着|Vm|增大，杂质点及其附近点局域态密度受到的影响.其中负能侧有一大一小2个共振峰，当

Vm=-0.31 eV,Vs=-0.25 eV

时，2个共振能隙分别为

Δ=-0.004 4 eV，Δ2=-0.002 8 eV，

其中能隙较大的共振峰高度随着杂质势的增大而升高.与之相反，较低的共振峰高度则先减小，后逐渐消失.当Vm=-0.35 eV时，2个共振峰变为一个峰，且峰的位置一直向零能点移动，最终越过零能点.整个变化过程，正能侧始终都未观察到的共振峰.只有在Vm>-0.35 eV时，才有不明显的共振峰出现.与负能侧趋势相同，向零能点移动.当能隙较大的共振峰越过零能位置后，逐渐靠近能隙边缘，峰值高度则逐渐减小.在磁性势变化过程中，当Vm=-0.37 eV，3个点的局域态密度在w=2.60 meV处，出现可观察的共振峰，当Vm=-0.40 eV，在w=-1.40 meV处，即在负能侧较高共振峰左边，又劈裂出一个峰,并且都向零能点处移动.

如图7,当Vm=-0.50 eV时，在w=-1.20 meV，w=1.60 meV，出现明显的共振峰;当|Vm|>0.50 eV,正负能侧2个杂质共振峰继续劈裂为4个峰，其中靠近能隙边缘的2个峰，逐渐远离零能位置.另外,靠近零能位置处的2个共振峰，则慢慢向零能中心方向移动，随着磁性势的增大，后又逐渐合变为一个杂质共振峰，继续劈裂，呈周期变化.由于磁性杂质存在而抑制共振峰的强度，峰值高度都逐渐降低.对于杂质点，当Vm→∞时，杂质点的局域态密度逐渐趋于零.

3 结论

本文采用两轨道四带紧束缚模型，研究了铁基超导体中单个磁性杂质对局域态密度的影响.调节磁性势Vm和非磁性势Vs的大小，计算出杂质点、最近邻点、次近邻点上的局域态密度与混合杂质势之间的关系，研究了磁性势大于(小于)非磁性势时，单个磁性杂质诱导的隙内束缚态，也发现了不同位置变化规律的杂质共振峰及其高度变化趋势.此外，本文发现在杂质点附近由于磁性杂质的存在导致在零能处产生共振峰，而且正负能侧的共振峰也受到抑制.随着磁性势的增强，零能处附近的诱导峰强度逐渐变弱，并劈裂为2个(多个)峰.本文发现在非磁性势Vs一定，磁性势Vm=|Vm|时局域态密度曲线基本相同，而且在一定的杂质势范围内，正负能侧杂质共振峰是对称的.磁性杂质在任何序参量下均产生2个(多个)杂质共振峰，与自旋上、下相联系.随着强度增加，两峰交错移动，呈周期性变化.在铁基超导体中，局域态密度LODS主要显较强杂质势的特征.