多层黑磷中厚度和应力依赖的能隙变化研究
琚伟伟, 李同伟, 雍永亮, 孙金锋
(河南科技大学物理工程学院, 洛阳 471023)
多层黑磷中厚度和应力依赖的能隙变化研究
琚伟伟, 李同伟, 雍永亮, 孙金锋
(河南科技大学物理工程学院, 洛阳 471023)
采用基于密度泛函理论的第一性原理方法研究了单层及多层黑磷晶体的能隙随层数和外加应力的变化.计算结果表明,体系能隙随着层数的增加而减小,当层数增加到10时,二维黑磷的能隙非常接近于其体材料值.层间的相互作用导致的能带劈裂是能隙减小的直接原因.应力对10层黑磷电子结构的影响也被研究.计算表明,压缩应力可以使10层黑磷从半导体转变为金属,而拉伸应力仅对能隙大小产生影响.
电子结构; 能隙; 第一性原理; 黑磷
1 引 言
具有原子厚度的二维材料,例如石墨烯,氮化硼以及二维过渡金属硫化物,表现出来的优异物理和化学性质使这些材料受到人们的广泛关注[1-5]. 人们已经知道石墨烯拥有众多优异性质,如高电子迁移率,高热导率,常温霍尔效应等,然而带隙的缺乏使它仅具有小的开关电流比,限制了它在实际器件中的应用. 而作为二维过渡金属硫化物代表之一的MoS2单层尽管拥有约1.8eV的直接带隙和相对高的开关比,然而它的载流子迁移率却远远低于石墨烯.
因此,寻找具有合适带隙且具有高载流子迁移率的材料成为一个非常重要的课题. 最近,两个研究组分别报道了一种新的二维材料—单层黑磷,这种材料同时具有直接带隙和高的载流子迁移率,可以克服石墨烯的不足,成为石墨烯的良好替代材料[6-8]. 黑磷(Black Phosphorus, BP)是磷的一种同素异形体,早在上世纪五十年代已经开始被研究[9-11]. BP具有类似石墨的层状结构,如图1(a)所示. 我们知道P原子的价电子排布是3s23p3,s轨道上的电子已经配对,p轨道上存在三个未配对电子,因此在BP中,每个P原子与周围的三个P原子形成共价键,每层均形成扭折的几何结构. 受到石墨烯研究的启发[1],从BP晶体中剥离出单层或多层BP并对其性质进行研究是一个非常有趣的课题. 采用类似剥离石墨烯的方法,张远波、陈仙辉教授研究组[6]以及Peide教授研究组[7]分别成功获得了纳米厚度的BP晶体. 他们发现二维BP晶体的能隙是直接能隙,这个特性让它的光学和光电性能同其它材料,包括硅和硫化钼相比有巨大的优势. BP的直接能隙可以增强它和光的直接耦合,让它成为未来光电器件(例如光电传感器)的一个备选材料. 另外,人们同时也发现二维BP晶体具有非常高的载流子迁移率. 因此,BP这一新型二维半导体材料是继石墨烯、二硫化钼之后的又一重要进展,为二维晶体材料家族增添了一位新成员[12-15].
实验和理论研究已经表明1到5层二维BP晶体的能隙与层数有直接的关系[16,17]. 但是,5层BP的能隙与体材料的值仍有一定的差距[17]. 当二维BP的层数达到多少时,其能隙以及电子结构与体材料基本相同?这是一个需要解决的问题. 应力对单层 BP晶体的影响也被研究. Peng等人发现单轴应力可以使单层BP的能隙出现直接-间接-直接的转变[18];Rodin的研究则表明,垂直于平面的单轴应力可以使单层BP出现半导体到金属的转变[19]. 然而在先前的研究中,人们很少关注双轴应力对二维BP的影响. 本文采用基于密度泛函理论的第一性原理方法研究了单层及多层(1到10层)BP晶体的几何及电子结构,我们发现二维BP的能隙与其层数有关,随着层数的减小,能隙单调增加. 10层BP的性质与体材料非常接近。双轴应力对10层BP电子结构的影响也被研究,结果表明双轴压缩应力可以使10层BP从半导体转变为金属. 这些结果对二维BP晶体的实验研究提供了理论依据.
2 计算模型和方法
2.1 计算模型
BP晶体具有层状结构,属于正交晶系,如图1(a)和(b)所示,空间群是Cmca,实验上获得的晶格参数如下[10,11]:a=4.3759 Å,b=3.3138 Å, c=10.477 Å,键角θ1=96.34°,θ2=102.09°. 单层BP的结构直接取自于晶体,在计算中采用超原胞模型,垂直于层面的方向取不少于15 Å的真空层,这个厚度保证了在周期性体系中两层之间的相互作用可以忽略[20]. 图1(c)给出了单层BP的俯视以及侧视图. 平面晶格常数a和b通过下面的方法进行优化:固定b,得到总能与a之间的函数关系,通过曲线拟合得到a;在此基础上,保持a不变,计算总能与b之间的关系,进而得到平衡晶格常数b. 弛豫得到的晶格常数a和b列在表1中. 对于双层BP,我们考虑了AA和AB两种堆垛方式. 对于AA堆垛,顶部单层BP被直接放置于底部的正上方,两层原子上下相互对应;对于AB堆垛,则采用BP晶体中的排列方式,可以看作把AA堆垛中底部一层沿a方向或者b方向平移晶格常数的一半. 计算表明,AB堆垛比较稳定[21],每个P原子的能量较之AA堆垛低3meV,AB堆垛的俯视和侧视图显示在图1(d)中. 对于3-10层BP薄膜,我们均采用ABAB…的堆垛方式,仍采用超原胞模型,晶格常数的优化方法与单层BP相同,得到的晶格常数以及BP晶体的晶格常数被总结在表1中.

layers12345678910bulka(Å)4 624 604 584 574 564 564 554 554 554 554 55b(Å)3 313 313 313 313 323 323 323 323 323 323 32
2.2 计算方法
体系的电子结构计算采用基于密度泛函理论的程序包Viennaabinitiosimulation package(VASP)[22]. 交换关联泛函采用PW91,电子和离子实之间的相互作用由投影缀加波(PAW)方法描述,相当多的研究表明,这种方法能够很好的描述低维体系的电子结构[23,24]. 波函数用平面波做展开,截止能量是320eV,总能的收敛判据是10-6eV. 在计算中,针对不同层数的BP晶体,从表1中选择相应的晶格常数固定不变,采用8×10×1的K点网格对原子位置进行优化,当Hellmann-Feynman力小于0.01eV/Å时停止优化[25]. 对于后续计算则采用21×27×1的K点,便于获得精确的电荷密度及能态密度.
3 计算结果和讨论
3.1 能隙与电子结构
二维BP的能隙随层数的改变被展示在图2中. 可以看到能隙随层数的增加单调减小,单层BP具有最大的能隙0.90 eV. 当层数增加到10时,能隙减小到0.11 eV,已经非常接近于体BP的能隙0.08 eV,因此我们仅对1-10层的二维BP进行了研究. 从图2中可以看到,能隙减小最快的是前面5层,尤其是从单层变为双层后,能隙减小了0.3 eV,即从单层时的0.90 eV变成双层时的0.60 eV. 5层BP薄膜的能隙仅0.28 eV,较之单层BP减小了0.62eV. 而从6层到10层,能隙减小的速度明显变慢. 能隙为什么会随着层数的增加而减小?减小的速度为什么逐渐变缓?通过对二维BP晶体能带结构和能态密度的分析,我们将对这些问题有更加深入的理解.
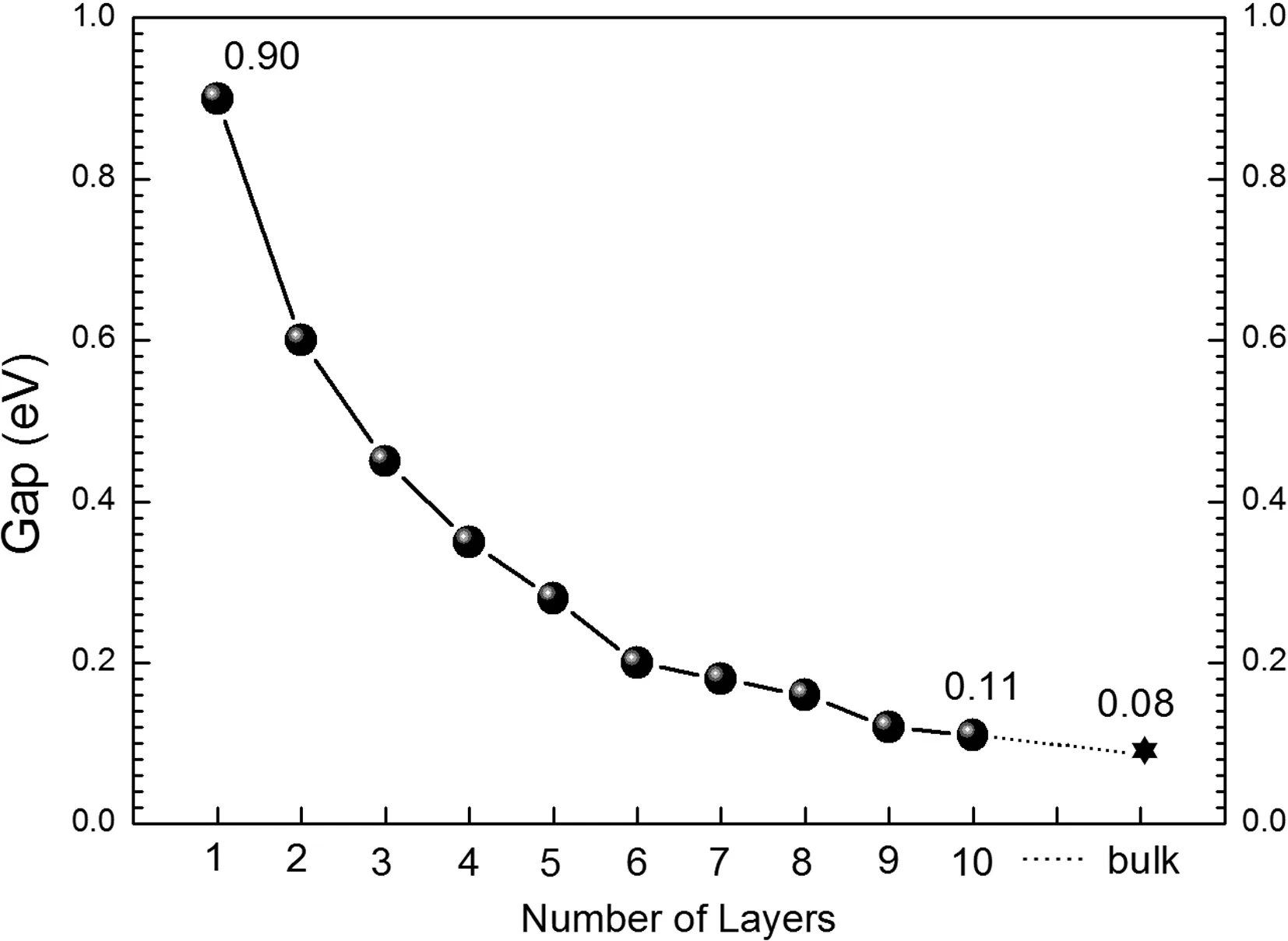
图2 多层黑磷中体系能隙与厚度之间的关系Fig. 2 Evolution of the band gap as a function of the number of layers in few-layer BP
从表1中可以发现,晶格常数b改变的非常小,从单层BP到体结构仅增加了0.01 Å,而a的变化比较显著,从单层到体结构减小了0.07 Å. 晶格常数a的显著改变可以被归因于层与层之间的相互作用,为了展现这种层间的作用,我们在图3中给出了几个具有代表作用的能带结构,分别对应于1, 2, 4, 6, 8, 10层的情况. 比较图3(a)和3(b),可以清楚的看到图3(a)中费米能级附近的每条能带在3(b)中均劈裂为两条. 例如价带(费米能级以下能量最高的那条能带)在Γ点处的劈裂可以达到0.6 eV. 同样,图3(a)中的能带在3(c)-3(f)中也产生了不同程度的劈裂,在Γ点处的劈裂值分别为0.8 eV,0.96eV,1.04 eV,1.13 eV. 也就是说,随着层数的增加,价带的劈裂也随着增加,导带的情况也是类似的. 价带和导带的劈裂是导致体系能隙随着层数的增加而减小的根本原因[17].
根据能带理论,当孤立原子聚合成晶体时,原子间的相互作用使孤立原子的能级展宽成为能带. 因此,当二维晶体中包含两层BP时,这两层之间的相互作用使一条能带劈裂为两条,劈裂的大小直接反应了两层BP间相互作用的大小. 在先前的研究中,人们认为BP晶体中层间的相互作用与石墨烯是相同的,属于范德瓦尔斯力. 然而,最近的一篇理论报道却指出[17],BP晶体层间的相互作用并不完全是范德瓦尔斯力,波函数的交叠对层间的相互作用也有非常重要的贡献. 我们在图4(a)和(b)中给出了双层BP的价带和导带的电荷密度图. 从图4(a)中可以清楚的看到,在两层之间,价带的电荷分布表现出类似成键态的性质,波函数产生了交叠,而导带的电荷分布并没有交叠,具有类似反键态的性质. 电子云交叠产生的相互作用比起范德瓦尔斯作用更强,导致了双层BP中Γ点处价带的显著劈裂. 层数的增加进一步加强了这种相互作用,因此使多层BP中产生了更大的劈裂.

图3 多层黑磷的能带结构.(a) 1层 (b) 2层 (c) 4层 (d) 6层 (e) 8层 (f) 10层Fig. 3 Band structures of few-layer BP. (a) 1-layer (b) 2-layer (c) 4-layer (d) 6-layer (e) 8-layer (f) 10-layer
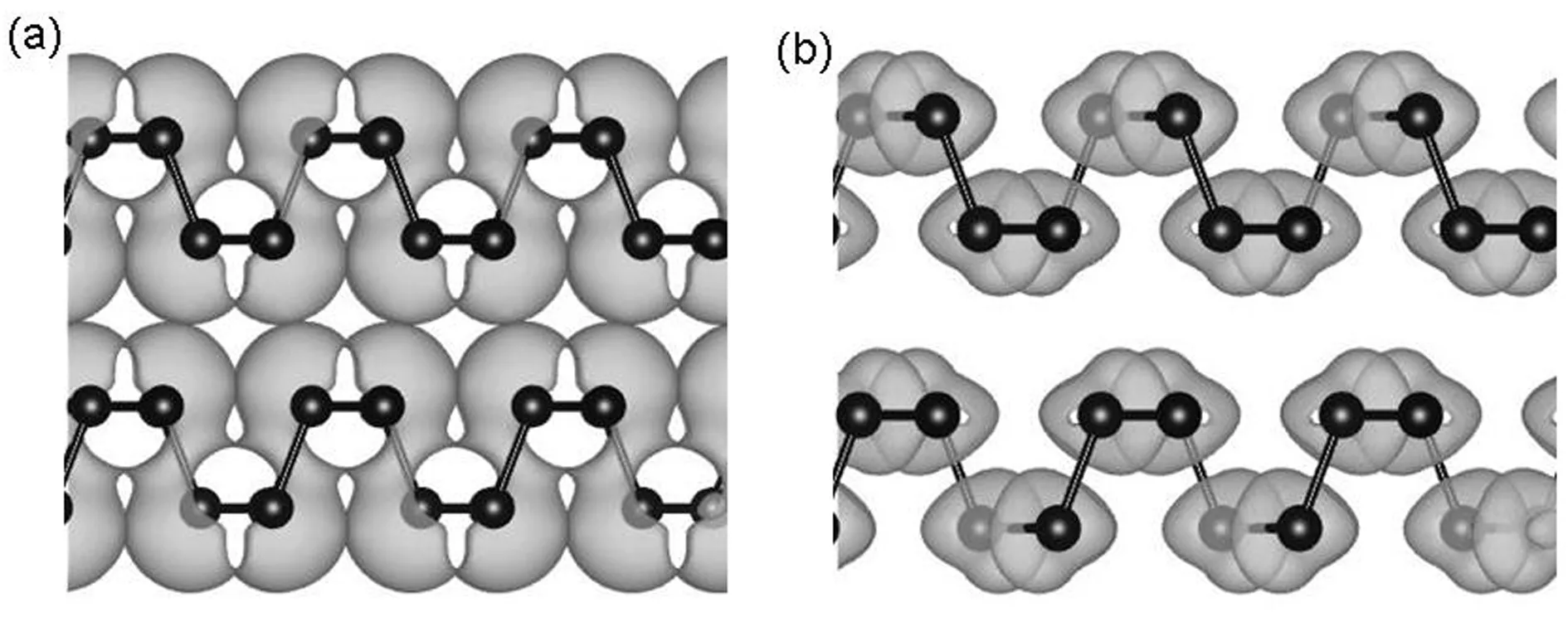
图4 双层黑磷中 (a) 价带 (b)导带的电荷密度图Fig. 4 The charge density of (a) valence band (b) conduction band in bilayer BP
为了对二维BP的电子结构有进一步的认识,我们在图5中给出了单层、10层以及BP体结构中P原子的p轨道投影态密度图(PDOS). 可以发现,对于每个轨道(px,py,以及pz),10层BP中P原子的价带分布与体材料是非常相似的. 这两种材料中,px和py轨道的价带位于-0.8 eV到-7 eV,pz态的价带则从费米能级一直延伸到-7 eV. 相比之下,单层BP的价带比较窄,仅仅延伸到-6.2 eV左右. 如果对px,py,以及pz轨道进行对比,可以发现px和py态是非常相似的,而pz态则与这两个态明显不同. 在费米能级附近,pz态有一个突出的峰,在图5(c)中我们用星号做了标记,这个峰来源于c方向与a、b两方向的不同对称性. 此外,我们也可以发现,pz态在费米能级附近的能隙明显小于px和py态,决定了体系的能隙,对体系电子结构的变化起主导作用.
3.2 应力诱导的半导体-金属转变
与体材料相比,二维材料更容易被拉伸或者压缩,因此,有关应力调控能隙以及应力下金属-绝缘转变的报道已经屡见不鲜[26,27]. 比如,对于MoS2,平面内的应力和平面外的应力均可以使这种二维材料发生半导体到金属的转变[27,28]. 受到这些报道的启发,我们研究了应力下多层BP电子结构的变化. 在没有应力即平衡态的情况下,不同层数BP的能隙已经被展示在图2中. 可以发现,10层BP体系具有最小的能隙,仅0.11 eV,因此,应力下10层BP的电子结构应该最容易被改变. 图6给出了不同应力下10层BP的能隙,这里应力指的是平面双轴应力,a方向和b方向同时被拉伸或者压缩,同时对原子位置进行优化,释放部分应力. 我们非常高兴的发现,在压缩应力的情况下,10层BP出现了半导体到金属的转变,即使应力小到1%,这种转变依然存在. 而对于拉伸的情况,能隙随着应力的增加逐渐增大,在应力达到5%时,能隙达到最大,0.48 eV,随后逐渐降低,直至应力达到10%,能隙降到0.19 eV,但未出现半导体到金属的转变.
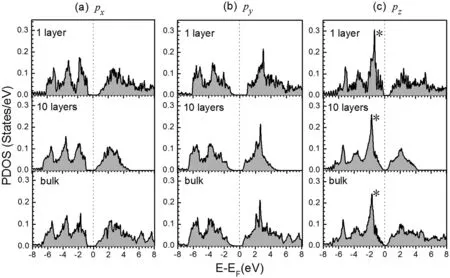
图5 单层、10层以及体黑磷中P原子的p轨道投影态密度图.(a) px轨道 (b) py 轨道 (c) pz轨道
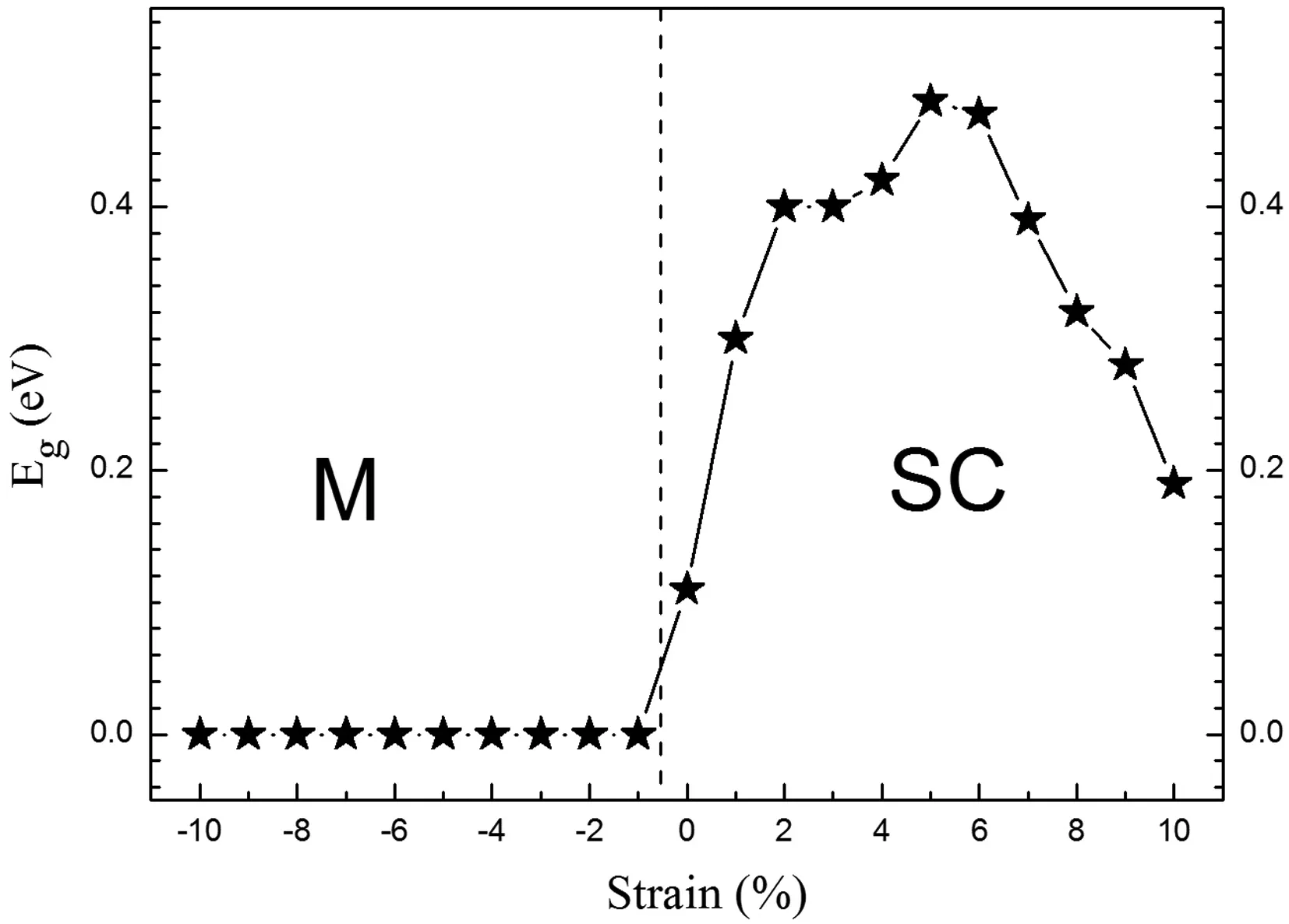
图6 10层黑磷体系的能隙与外加应力之间的关系, M代表金属,SC代表半导体Fig. 6 Band gap Eg with respect to the epitaxial strain, which varies from 0 to 10% in 10-layer BP
图7展示了四种不同应力下10层BP的能带结构图,分别对应于拉伸应力1%,10%以及压缩应力-1%和-10%. 比较拉伸应力下的能带结构(图7(a)和7(b))与平衡态的能带结构(图3(f)),可以发现图7(a)和图3(f)非常相似,而图7(b)中费米能级以上的两组能带(图中标记为A和B)产生了明显的分离,但体系依然保持半导体的电子结构. 在拉伸应力下,P-P键长的增加导致每组能带的色散变小,A组和B组能带的分离可以被归结于这个原因. 压缩应力则产生了明显不同的变化,比较图7(c)和图7(d),P-P键长的减小使能带的色散显著增加. 从图7(d)中可以看到在10%的压缩应力下,Γ点,Y点和X点附近能带均通过了费米能级,导致了体系半导体到金属的转变.
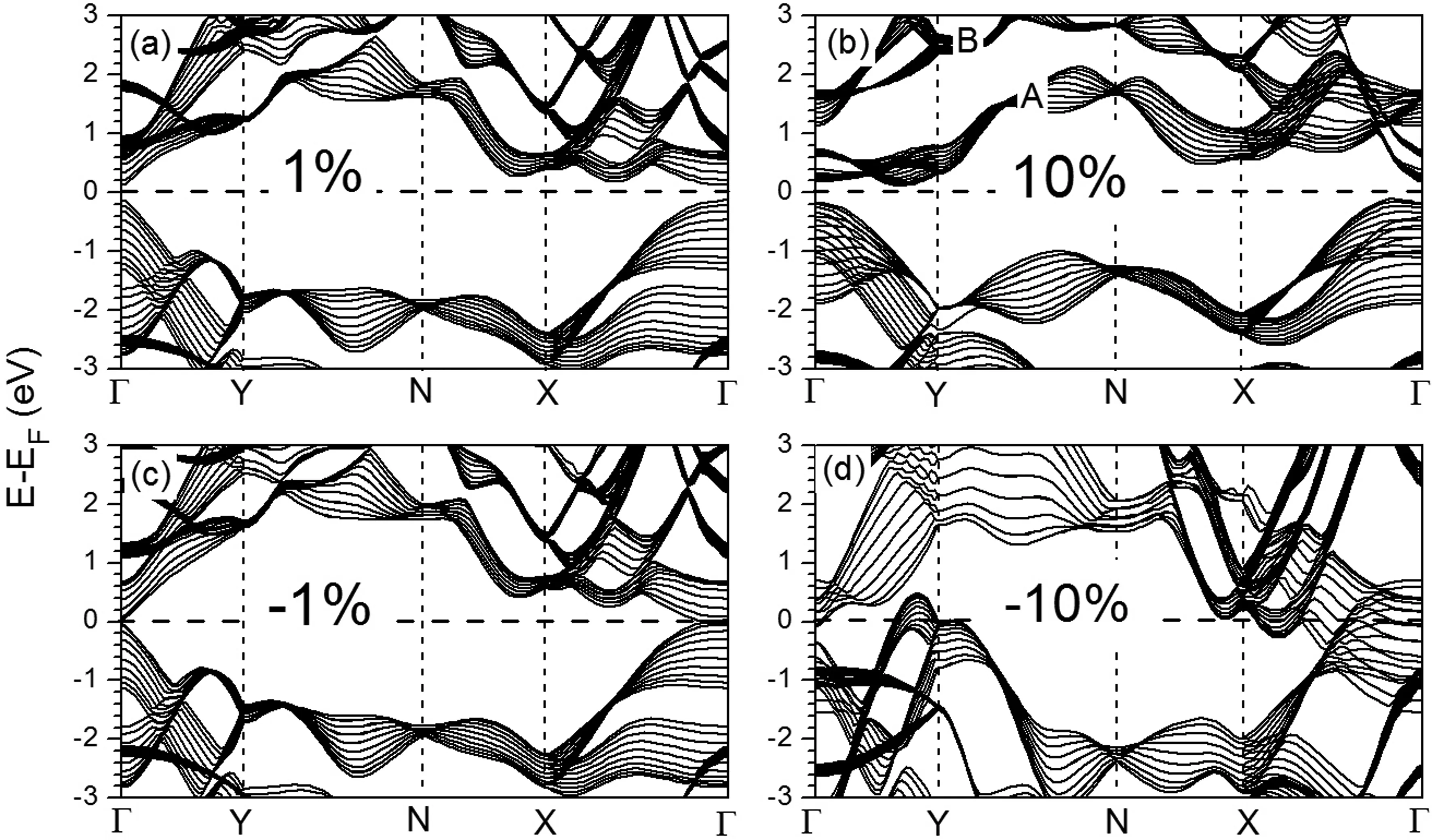
图7 不同应力下10层黑磷的能带结构. 1%和10%代表相应大小的拉伸应力,-1%和-10%代表相应大小的压缩应力Fig. 7 Band structures of 10-layer BP with different strains. 1% and 10% stand for the tensile strain, and -1% and -10% stand for the compressive strain
4 结 论
利用第一性原理计算研究了单层以及多层BP晶体的电子结构和应力作用对其电子结构的影响. 计算结果表明,BP的能隙随着层数的增加而减小,单层BP具有最大的能隙,约0.90 eV;10层BP的能隙减小到0.11 eV,非常接近于体材料的值. 层与层之间的相互作用导致的能带劈裂是能隙减小的直接原因. P原子的轨道投影态密度表明pz态决定了二维体系能隙,对电子结构的变化起主导作用. 此外,我们也研究了平面双轴应力对10层BP电子结构的影响,结果表明,压缩应力可以使体系发生半导体到金属的转变,而拉伸应力仅改变了能隙的大小. 我们的研究为二维BP晶体在光电器件中的应用提供了理论依据.
[1] Novoselov K S, Geim A K, Morozov,etal. Electric field effect in atomically thin carbon films [J].Science, 2006, 206: 666.
[2] Rader O, Varykhalov A, Sánchez-Barriga J,etal. Is there a rashba effect in graphene on 3dferromagnets? [J].Phys.Rev.Lett., 2009, 102: 057602.
[3] Barone V, Peralta J E. Magnetic boron nitride nanoribbons with tunable electronic properties [J].NanoLett., 2008, 8: 2210.
[4] Li W, Zhang G, Guo M,etal. Strain-tunable electronic and transport properties of MoS2nanotubes [J].NanoRes., 2014, 7: 518.
[5] Duerloo K N, Li Y, Reed E J. Structural phase transitions in two-dimensional Mo- and W-dichalcogenide monolayers [J].Nature.Commun., 2014, 5: 4214.
[6] Li L K, Yu Y, Ye G J,etal. Black phosphorus field-effect transistors [J].NatureNanotech., 2014, 9: 372.
[7] Liu H, Neal A T, Zhu Z,etal. Phosphorene: an unexplored 2D semiconductor with a high hole mobility [J].AcsNano, 2014, 8: 4033.
[8] Reich E S. Phosphorene excites materials scientists [J].Nature, 2014, 506: 19.
[9] Keyes R W. The electrical properties of black phosphorus [J].Phys.Rev., 1953, 92: 580.
[10] Takao Y, Morita A. Electronic structure of black phosphorus: tight binding approach [J].Phys. B, 1981, 105: 93.
[11] Brown A, Rundqvist S. Refinement of the crystal structure of black phosphorus [J].ActaCryst., 1965, 19: 684.
[12] Li W, Zhang G, Zhang Y W. Electronic properties of edge-hydrogenated phosphorene nanoribbons: a first-principles study [J].J.Phys.Chem. C, 2014, 118: 22368.
[13] Liu Y, Xu F, Zhang Z,etal. Two-dimensional mono-elemental semiconductor with electronically inactive defects: the case of phosphorus [J].NanoLett., 2014, DOI: 10.1021/nl5021393.
[14] Guan J, Zhu Z, Tománek D. Phase coexistence and metal-insulator transition in few-layer phosphorene: a computational study [J].Phys.Rev.Lett., 2014, 113: 046804.
[15] Low T, Roldán R, Wang H,etal. Plasmons and screening in monolayer and multilayer black phosphorus [J].Phys.Rev.Lett., 2014, 113: 106802.
[16] Zhang S, Yang J, Xu R,etal. Extraordinary photoluminescence and strong temperature/angle-dependent raman responses in few-layer phosphorene [J].AcsNano, 2014, 8: 9590.
[17] Qiao J, Kong X, Hu Z X,etal. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus [J].NatureCommun., 2014, 5: 4475.
[18] Peng X, Wei Q, Copple A. Strain-engineered direct-indirect band gap transition and its mechanism in two-dimensional phosphorene [J].Phys.Rev. B, 2014, 90: 085402.
[19] Rodin A S, Carvalho A, Castro Neto A H. Strain-induced gap modification in black phosphorus [J].Phys.Rev.Lett., 2014, 112: 176801.
[20] Payne M C, Teter M P, Allan D C,etal. Iterative minimization techniques forabinitiototal-energy calculations: molecular dynamics and conjugate gradients [J].Rev.Mod.Phys., 1992, 64: 1045.
[21] Dai J, Zeng X C. Bilayer phosphorene: effect of stacking order on bandgap and its potential applications in thin-film solar cells [J].J.Phys.Chem.Lett., 2014, 5: 1289.
[22] Kresse G, Furthmuller J. Efficient iterative schemes forabinitiototal-energy calculations using a plane-wave basis set [J].Phys.Rev. B, 1996, 54: 11169.
[23] Blochl P E. Projector augmented-wave method [J].Phys.Rev. B, 1994, 50: 17953.
[24] Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method [J].Phys.Rev. B, 1999, 59: 1758.
[25] Stich I, Car R, Parrinello M,etal. Conjugate gradient minimization of the energy functional: a new method for electronic structure calculation [J].Phys.Rev. B, 1989, 39: 4997.
[26] Johari P, Shenoy V B. Tuning the electronic properties of semiconducting transition metal dichalcogenides by applying mechanical strains [J].AcsNano, 2012, 6: 5449.
[27] Scalise E, Houssa M, Pourtois G,etal. Strain-induced semiconductor to metal transition in the two-dimensional honeycomb structure of MoS2[J].NanoRes., 2012, 5: 43.
[28] Su X, Zhang R, Guo C,etal. Band engineering of dichalcogenide MX2nanosheets (M=Mo,W and X=S,Se) by out-of-plane pressure [J].Phys.Lett. A, 2014, 378: 745.
Band gap of few-layer black phosphorus modulated by thickness and strain
JU Wei-Wei, LI Tong-Wei, YONG Yong-Liang, SUN Jin-Feng
(College of Physics and Engineering, Henan University of Science and Technology, Luoyang 471023, China)
By using the first principle calculations based on density functional theory, the band gap of few-layer black phosphorus (BP) is studied. The band gap depends on the layer number of black phosphorus and the epitaxial strain. The calculated results show that the band gap will decrease with the increase of layer number in few-layer BP. The band gap of few-layer BP will be close to the value of bulk BP when layer number is up to 10. The reason that the band gap decreases is the splitting of energy bands induced by the inter-layer interactions. The influence of the strain on the electronic structures of 10-layer BP is investigated. The calculations suggest that the compressive strain results in a semiconductor-metal transition for 10-layer BP, whereas the tensile strain only affects the values of band gaps.
Electronic structure; Band gap; First principle; Black phosphorus
103969/j.issn.1000-0364.2015.02.027
2014-10-17
国家自然科学基金(11404096, 11304080, U1404609)
琚伟伟(1980—),女,河南济源市人,博士,主要从事材料的电子结构的理论研究.E-mail: hnjww@126.com
O472+.4
A
1000-0364(2015)02-0329-07

