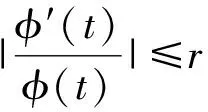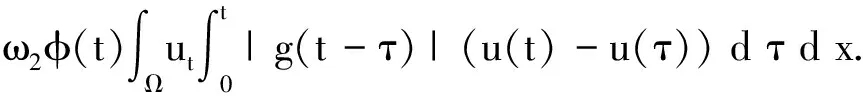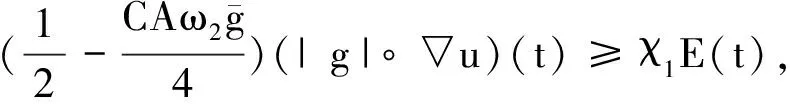一类带有记忆核的黏弹性方程解的能量衰减估计

岳香英, 蒲志林

(四川师范大学 数学科学学院, 四川 成都 610066)

1 引言及预备知识

本文考虑以下带有记忆项的黏弹性方程的柯西问题

utt(x,t)-Δu(x,t)+

u(x,0)=u0(x),

ut(x,0)=u1(x),x∈Ω,

(1)

其中,Ω是Rn(n∈N)中的有界区域,u0、u1为初值,g是定义在Ω上的函数,是方程的记忆项,称为记忆核,也叫松弛函数.

已有大量的学者对黏弹性方程的动力学行为进行了研究,例如文献[1-5].从已知的研究结果中知道,当g≡0时,系统的能量值为常数,当g≠0时,以下是一些关于黏弹性系统解的渐近行为的结果:文献[6-7]确定了黏弹性方程的解的存在性,并表明随着时间趋于无穷,黏弹性系统的解趋于零,但是并没有计算出明确的衰减率.当记忆核g呈g=e-αt即指数衰减的形式时,文献[8-9]得出了非线性黏弹性方程解的指数衰减率.文献[10-14]的研究结果表明在有界区域上,黏弹性方程解的衰减率依赖于记忆核g的衰减率,即当记忆核g呈指数衰减时,方程的解也是呈指数衰减,而当记忆核g呈多项式衰减时,方程的解也以相同的衰减率呈多项式衰减.Rivera等[15]研究了方程

(2)

其中A是某个Hilbert空间上的正自伴算子.证明了当0≤α<1时,方程记忆项g的衰减不足以使方程的解产生指数衰减的稳定形式,但在一定的条件下,可以使方程的解呈多项式衰减.

在之前的研究中,记忆函数g都有衰减的特性.关于记忆函数g都有如下的假设

g(0)>0,g′(t)≤-αg(t), ∀t≥0,

(3)

其中,α>0.上述假设条件太过严苛,已有许多文献在讨论放宽这一假设[16-21].特别地,文献[18]在Rn中对记忆函数g做了如下假设

g(0)>0,g′(t)+αg(t)≥0, ∀t≥0. (4)

在这个假设中,g′(t)可以取正值,即说明记忆函数g可以适当递增,而不是一直衰减的,并且在该假设条件下,得到了方程的解是呈多项式衰减的.文献[19]关于记忆函数g做了如下假设:

g∈W2,1(R+)∩C2(R+),g(0)>0,

(5)

其中α和Cg是正常数.在该假设下，g、g′和g″可以变号,所得结果是当记忆核g呈指数衰减时,方程的解也是呈指数衰减,而当记忆核g呈多项式衰减时,方程的解也以相同的衰减率呈多项式衰减.

本文受文献[18-19]启发,不再局限于g>0以及g具有一致衰减特性,建立了新的假设,并构造了方程(1)的能量泛函.对能量泛函进行估计,得到方程(1)的解的渐近性,以及在|g|呈指数衰减时,方程的解依据 φ(t)的不同呈相应的衰减方式.

本文对记忆核 g作如下假设:

( C1)g:R+→R是一个可微函数,满足

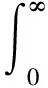
(C2) 存在可微函数φ>0以及常数r>0和h>0满足

|g(t)|′≤-φ(t)|g(t)|,t≥0,

φ′(t)≤0, ∀t≥0.

该假设拓宽了假设(4)的应用范围,即g的符号不要求一定为正,也可以为负,同时弱化了假设(5)中g二阶可导的要求.相较于假设(4)和(5),本文的假设条件应用更为广泛和一般.

记

引理 1.1[16]若假设(C1)和(C2)成立,且

u0∈H1(Ω),u1∈L2(Ω),

则问题(1)存在唯一的解满足:

u∈C([0,∞),H1(Ω)),

ut∈C([0,∞),L2(Ω)).

引理 1.2[18]当1≤p

存在一个常数C=C(n,p),使得

‖u‖p*≤C‖▽u‖p, ∀u∈W1,p(Ω). (6)

定义能量泛函

其中

引理 1.3若u是方程(1)的解,则能量泛函满足

(7)

其中N和H是正常数.

证明对能量泛函两边求导,可得

E′(t)=(▽u(t),▽ut)+

(8)

其中

(9)

对(9)式的第二项进行估计,则存在常数N>0和H>0,

dxdτ≤

(10)

由于|g|是非增函数，所以

|g(t)|≤|g(0)|=g(0)=K.

对(8)式第二项进行估计

由(8)～(11)式可得到(7)式.

2 能量衰减估计

引理 2.1若u是系统(1)的解,定义辅助泛函

在假设(C1)和(C2)条件下,则存在某个常数ξ1>0使得

(12)

证明对Ψ1(t)求导,可得

(13)

由(1)式可得

(14)

所以

(15)

由(5)式可得

C‖▽u‖2‖ut‖2≤

(16)

对(14)式的第二项进行估计,可得

|▽u(t)|)dτ)2dx.

(17)

由Young不等式可得

|▽u(t)|)dτ)2dx≤

(18)

由(15)～(18)式可得

引理 2.2若u是系统(1)的解,定义辅助泛函

(u(t)-u(τ))dτdx,

则存在某个常数ξ2,在t≥0时满足

(20)

证明直接对Ψ2(t)求导,可得

(u(t)-u(τ))dτdx-

(21)

其中

(22)

对于(21)式中的第二项,由(1)式可得

对于(21)式中的第一项,可得

(24)

对于(23)式中的第一项,可得

(25)

对于(23)式中的第二项,可得

|▽u(t)|)dτ)2dx+

由Young不等式及假设(C2)可得

(27)

将(22)～(27)式代入(21)式,则(20)式成立.

引理 2.3假设(C1)和(C2)成立,构造辅助泛函

F(t)=E(t)+ω1Ψ1(t)+ω2Ψ2(t).

(28)

取适当的2个正常数χ1、χ2,使其满足

χ1E(t)≤F(t)≤χ2E(t),t≥t0,

(29)

其中t0是足够大的值,使得ω1、ω2充分小.

证明把E(t)、Ψ1(t)、Ψ2(t)、Ψ3(t)代入(24)式,可得

(30)

由Cauchy-Schwarz不等式、Young不等式和(6)式可得

(31)

和

(32)

由假设(C2)知φ(t)为单调减函数,则有

φ(t)≤φ(0)=A.

(33)

将(31)～(33)式代入(30)式可得

同理可得

(35)

和

(36)

下面将(33)～(35)式代入(28)式,可得

其中ω1和ω2充分小,可得

F(t)≥χ1E(t),t≥t0,χ1>0.

(38)

联立(34)和(37)式,可得到结论.

定理 2.1假设(C1)和(C2)成立,且u0∈H1(Ω),u1∈L2(Ω),以及引理1.3的条件成立,则存在正常数P和p,使得

证明对(28)式求导,并由(7)、(12)、(20)式及假设(C2)可得

-[ω2(1-m-ξ2(r+1))-

hN]φ(t)(|g|∘▽u)(t).

(39)

由假设(C2)知

φ(t)(|g|∘▽u)(t)≤

|▽u(τ)-▽u(t)|2dτdx+

φ(t)(|g|∘▽u)(t)≤

hN]φ(t)(|g|∘▽u)(t),

(40)

所以

F′(t)≤-[ω2(1-m-ξ2(r+1))-

hN]φ(t)(|g|∘▽u)(t).

(41)

选择合适的ξ1和ξ2使得

若选定ξ1和ξ2,选择合适的ω1和ω2满足条件

(42)

使得

ω2(1-m-ξ2(r+1))-

因为g是连续且g(0)>0,所以对任意的t≥t0>0有

(43)

取

P0=min{k1,k2,k3},

则可得

F′(t)≤-P0φ(t)E(t).

又由(29)式可得

(44)

对(44)式在(t0,t)上积分可得

(45)

又由(29)和(45)式可得

(46)

故定理2.1得证.