一类二阶微分方程的几个振动准则

覃桂茳, 冀占江*, 卢振坤

(1. 梧州学院 信息与电子工程学院, 广西 梧州 543002; 2. 梧州学院 广西高校图像处理与智能信息系统重点实验室, 广西 梧州 543002;3. 广西民族大学 信息科学与工程学院, 广西 南宁 530006)

1 预备知识

近来,中立型泛函方程的振动性引起了国内外学者的极大兴趣和广泛关注[1-17].笔者研究具有拟线性中立项的二阶微分方程

{a(t)|[x(t)+p(t)xα(τ(t))]′|β-1[x(t)+

p(t)xα(τ(t))]′}′+q(t)f(|x(δ(t))|γ-1x(δ(t)))=

0,t≥t0

(1)

的振动性.为了叙述的方便，做如下假设:

(A1) 实常数0<α≤1为2个正奇数的商,而β>0和γ>0为任意实常数；函数a∈C1([t0,+),(0,+))且a-1/ β(t)dt=+；p,q∈C([t0,+),R)且0≤p(t)<1，q(t)>0.

(A2)τ,δ:[t0,+)→(0,+)为时滞函数,并且满足：τ(t)≤t且；且δ′(t)>0.

(A3)f∈C(R,R),且当u≠0时，uf(u)>0,f(u)/u≤L,其中L>0为常数.

关于方程(1)的解及其振动性的定义,可参见文献[1-14].对于方程(1)的特殊情形的振动性,最近出现了一些研究成果.如文献[10]研究了一类二阶广义的Emden-Fowler型微分方程(即方程(1)在α=1且f(u)=u时的特殊情形)振动性,得到了相应方程振动的若干充分条件，其中1个主要定理为定理A.

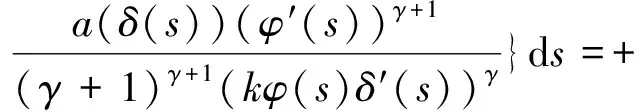
则方程

{a(t)|z′(t)|β-1z′(t)}′+

q(t)|x(δ(t))|γ-1x(δ(t))=0,t≥t0

是振动的,其中k>0为常数,函数Q(t)=q(t)[1-p(δ(t))]γ,z(t)=x(t)+p(t)x(τ(t)).

这是文献[10]中的定理2.2,也是其主要结果,由此定理及其证明的基本思路就可以得到该方程的各种类型的振动准则.但注意到,文献[10]定理A中的条件“a′(t)≥0”是较为严格的,而且当β<γ时,作者没有得到方程(3)的振动性判别准则.

对具有非线性中立项的情形,最近,文献[11]研究了方程(1)当γ=1时的振动性,得到如下结果.

定理 B[11]设条件(A2) 成立,β>0为2个正奇数的商,如果存在函数φ∈C1([t0,+),(0,+)),使得当0<β≤1时有

当β>1时有

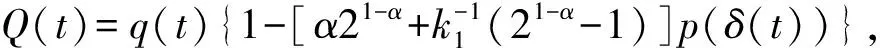
{a(t)[(x(t)+p(t)xα(τ(t)))′]β}′+

q(t)f(x(δ(t)))=0,t≥t0

(2)

是振动的.

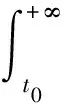
2 方程振动的判别定理

引理 1设X、Y为非负实数，则当0<λ≤1时,Xλ+Yλ≤21- λ(X+Y)λ.

证明由函数f(x)=xλ(0<λ≤1)的凹凸性容易得到.

下面的引理2～4是众所周知的，故略去其证明.

引理 2(Bernoulli不等式) 对任意实数x>-1，当0≤r≤1时，(1+x)r≤1+rx，当r≤0或r≥1时，(1+x)r≥1+rx.

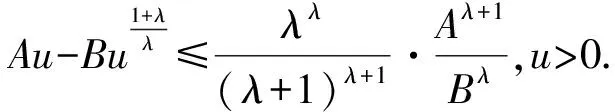
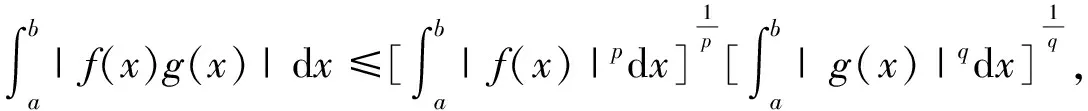
令

z(t):=x(t)+p(t)xα(τ(t)),

定理 1设(A1)～(A3)成立，若存在函数φ∈C1([t0,+),(0,+))及常数ω≥0，使得

(3)

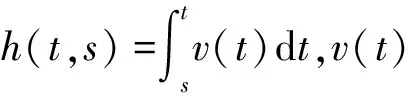
Q(t)=

函数

而t2≥t0，k>0及m>0都是常数，则方程(1)是振动的.

证明反证法.设方程(1)存在一个非振动解x(t).首先，若x(t)最终为正，则∃t1≥t0，使得当t≥t1时，x(t)>0，x(τ(t))>0，x(δ(t))>0.方程(1)中p(t)>0，可得z(t)=x(t)+p(t)x(τ(t))≥x(t)>0(t≥t1)，且利用(A3)条件，则有

[a(t)|z′(t)|β-1z′(t)]′≤

-Lq(t)xγ(δ(t))<0,

(4)

利用条件(A1)，由(4)式容易得到

z′(t)>0,t≥t1.

利用条件(A2)以及[a(t)(z′(t))β]′≤0,得

a(t)(z′(t))β≤a(δ(t))(z′(δ(t)))β,

(5)

分别利用引理1及引理2可得

x(t)=z(t)-p(t)xα(τ(t))=

z(t)-p(t)[1+xα(τ(t))]+p(t)≥

z(t)-21-αp(t)[1+x(τ(t))]α+p(t)≥

z(t)-21-αp(t)[1+αx(τ(t))]+p(t)=

z(t)-21-ααp(t)x(τ(t))+(1-21-α)p(t)≥

z(t)-21-ααp(t)z(τ(t))+(1-21-α)p(t)≥

(1-21-ααp(t))z(t)-(21-α-1)p(t).

(6)

定义函数w(t)为：

(7)

则w(t)>0(t≥t1).利用(4)～(6)式，由(7)式可推得

(8)

由于z(t)>0,z′(t)>0(t≥t1)，所以

z(δ(t))≥z(δ(t1))=k,t≥t1,

(9)

其中常数k>0.于是，利用(7)、(9)式和函数Q(t)的定义，由(8)式可得

(10)

(i) 若β=γ，则z(γ-β)/β(δ(t))=1.

(ii) 若β<γ，则由(9)式知

z(γ-β)/β(δ(t))≥k(γ-β)/β.

于是存在常数m>0，当t2≥t1充分大时，有

即z(γ-β)/β(δ(t))≥[mΘ(δ(t))](γ-β)/β.综上所述，并注意到函数θ(t)的定义，由(9)式得

(11)

现将(10)式中的t改成s，两边同乘以hω(t,s)，再从t2到t(t≥t2)积分得

(12)

为消去w(s)，分别取

利用引理3得

经整理得

将上式代入(12)式得

从而得到

hω(t,t2)w(t2)≤hω(t,t0)w(t2),

进而有

(13)

这与(3)式矛盾.

其次，若x(t)为方程(1)的最终负解，则令y(t)=-x(t)，于是方程(1)就化为

{a(t)|[y(t)+p(t)yα(τ(t))]′|β-1[y(t)+

p(t)yα(τ(t))]′}′+

q(t)f*(|y(δ(t))|γ-1y(δ(t)))=0,

t≥t0，

(14)

其中f*(u)=-f(-u)，显然f*(u)与f(u)具有相同性质，由于y(t)为方程(14)的最终正解，同理可得到与(3)式矛盾.定理证毕.

推论 1设(A1)～(A3)成立，若存在函数φ∈C1([t0,+),(0,+))，使得

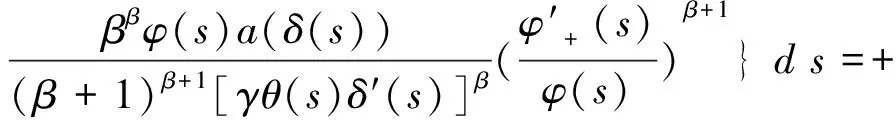
其中常数t2、k、m及函数Q(t)和θ(t)的定义都如定理1，则方程(1)是振动的.

证明在定理1中取ω=0即得.

推论 2设(A1)～(A3)成立，如果

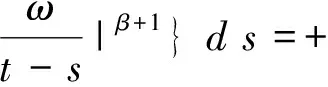
其中常数t2、k、m及函数Q(t)和θ(t)的定义都如定理1，则方程(1)是振动的.

证明在定理1中取v(t)=1即得.

推论 3设(A1)～(A3)成立，如果

其中常数t2、k、m及函数Q(t)和θ(t)的定义都如定理1，则方程(1)是振动的.

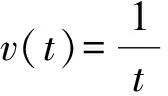
推论 4设(A1)～(A3)成立，如果

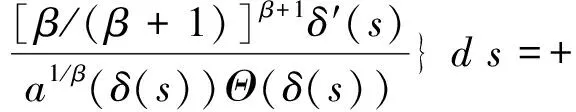
则方程

[a(t)|x′(t)|β-1x′(t)]′+

q(t)|x(δ(t)|β-1x(δ(t)=0,t≥t0(15)

是振动的，其中常数t2、k、m及函数Q(t)和θ(t)的定义都如定理1.

证明在方程(1)中令f(t)=t,β=γ且p(t)≡0，并在推论1中取φ(t)=Θβ(δ(t))即得.

若定理1中条件(3)式不成立，则方程(1)的振动准则如下.

定理 2设(A1)～(A3)成立，若∃φ(t)∈C1([t0,+),(0,+))及函数ζ(t)∈C([t0,+),(0,+))，使得对∀u≥t2≥t0有

(16)

(17)

且ζ(t)满足

(18)

其中函数Q(t)及θ(t)的定义同定理1，则方程(1)是振动的.

证明证明过程的前面部分同定理1，同样得到(12)和(13)两式.首先，根据(13)式，当t≥u≥t2≥t0时，则有

考虑到(17)式，得到

ζ(u)≤w(u)，

(19)

且有

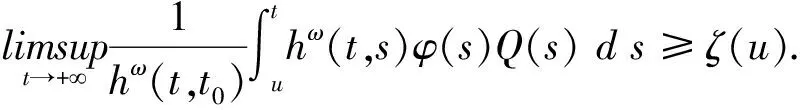
现将(12)式的移项变形得

利用(20)式可得

其中M0=w(t2)-ζ(t2)是常数，至此可以断定：

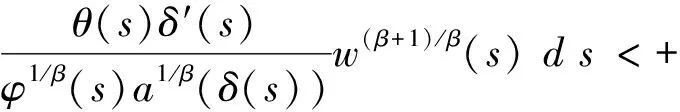
(21)

于是

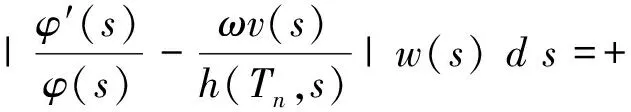
故对充分大的正整数n有

对ε∈(0,1)和充分大的正整数n，进一步得到

1-ε>0.

(22)

同时，应用引理4中的Hölder不等式获得

(23)

利用(22)和(23)式可得

这与

矛盾,所以(21)式成立.于是，注意到(19)和(20)式，得

这与(17)式矛盾.定理证毕.

注 1在定理1和定理2中,选取适当的不同的函数φ(t)和h(t,s),就可得到含非线性中立项的方程(1)的种种不同的振动准则.

3 应用举例

给出下面的例子来说明主要结果.

例 1考虑二阶时滞微分方程

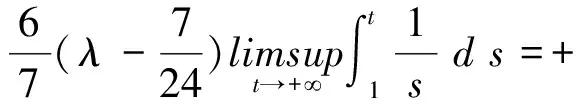
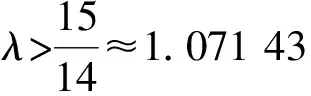
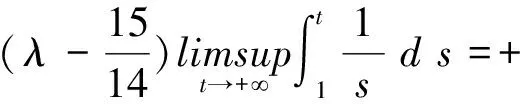
所以当λ>1.071 43时,方程(24)是振动的.这说明，当α=1时,本文的结果要比文献[7]中的有关结论要“精细”得多.

例 2考虑下列微分方程

(25)

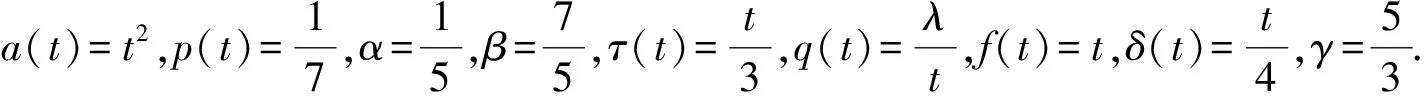
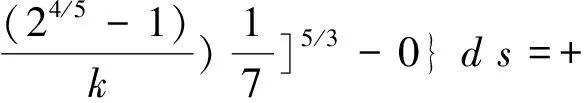
根据推论1，方程(25)是振动的.

注 3因为微分方程(25)是具有非线性中立项的，并且β≠γ，δ(t)<τ(t),所以文献[1-16]中定理的有关结论对方程(25)都不适用.

4 结论

从研究的结果可以看出，本文的定理不仅比现有部分参考文献的结论做得更精细了，还在定理推广、改进中丰富了现有文献中的结果.

致谢梧州学院校级科研项目(2017C001)对本文给予了资助,谨致谢意.