分数阶黏性方程MHD流的数值方法

张 俊

(贵州财经大学 数统学院, 贵州 贵阳 550025)

MHD方程是等离子体流体动力学理论的重要方程组，它能描述电磁流体状态参量随时间演化的过程[1-3]，它的基本方程由流体力学中的Navier-Stokes方程和电磁学中的Maxwell方程组成.Khan等[4]在研究不稳定的不可压MHD流时，得到了

其中,V是流速场，T是柯西力张量，ρ是流体密度，J是电流密度,B是总磁场.

Rivlin等[5]、Siddiqui等[6]、Palade等[7]和Rossihin等[8]对于T的不同定义，同时考虑到二阶流体满足的不同条件和，得到了一个含有黏性项的磁流体方程

这里η>0是无纲量的黏性参数,μ是跟磁场、密度有关的正参数.

由于方程解的复杂性，一般情况下很难求出其解析解,只能求其数值解，因此研究磁体流方程高效数值方程显得尤其重要.对于不含分数阶黏性项的MHD方程，已经有了大量的研究结果，如WENO有限差分格式、高阶G-K格式和四步龙格-库塔法等.对于上述含分数阶项的MHD方程，文献[9]分析了方程的准确解，但仍然缺乏高效数值方法.受文献[10]的启发，准备用差分法来离散分数阶项，提出一种高效的数值方法来处理黏性MHD方程.

本文构造了一种求解MHD型黏性分数阶方程的数值格式，所提的格式在时间方向差分，空间方向用Legendre-Galerkin谱方法，分析了格式在时间方向的稳定性，并得到了格式的整体误差估计O(Δt2-β+N1-m)，数值实验验证了理论证明.

1 黏性MHD型分数阶方程

这里考虑如下的MHD分数阶方程

(1)

和初值条件

(2)

以及边界条件

u(-L,t)=u(L,t)=0,t∈(0,T],

(3)

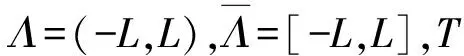
2 时间有限差分方案与稳定性分析

用有限差分方案离散分数阶导数，类似于Lin等[10]对分数阶项的处理，有如下的等式成立：

cDβt∂2xu(x,tn+1)=

[(j+1)1-β-j1-β]+rn+1=

其中

aj=(j+1)1-β-jβ,

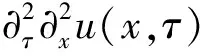
对于第一步,考虑如下格式

(4)

当n≥1,考虑如下格式

an∂2xu0)=0,

(5)

其中

定理 2.1时间离散格式(4)和(5)满足下列估计式，即

(6)

(7)

其中

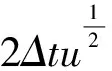
(6)式得证.

由Cauchy-Schwarz不等式可得

丢掉一些正项有

注意

因此有

所以

E(un+1)≤E(u1)+

定理得证.

3 空间Lagrange-Galerkin谱离散

这里将构造(4)和(5)式空间谱离散方案，考虑到该问题的边界条件，因此将用Lagrange-Galerkin谱方法对空间进行离散，定义N次多项式空间ΡN(Λ)，让

由文献[11]可知下面的误差估计式成立：

‖u-πNu‖0≤N-m‖u‖m,

∀u∈Hm(Λ),m>0,

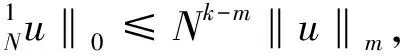
∀u∈Hm(Λ),m>0,k=0,1.

(8)

对于第一步：

(10)

其中

lj(x)是拉格朗日插值多项式.

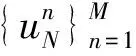
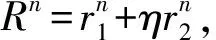
由Taylor展开式可知

(11)

再定义误差函数

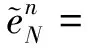
enN=u(tn)-unN.

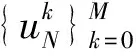
E(enN)≤c(Δt2-β+N1-m),

k=0,1,2,…,M.

(12)

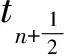
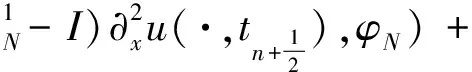
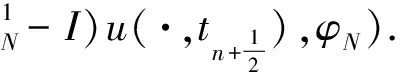
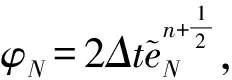
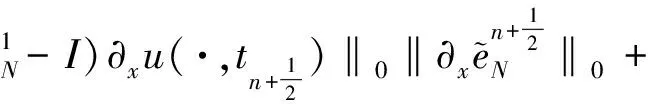
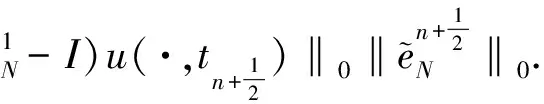
丢掉一些正项，由Young不等式可知

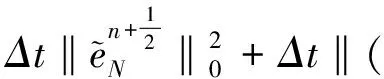
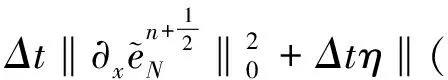
两边分别对n=1,2,…,k求和，注意到(8)和(11)式有

同样的方法，易知

由离散的Gronwall引理得

即可得(12)式.

4 数值结果

下面验证数值算法的有效性.为了得到刚度阵和质量阵，将

因很难得到方程的解析解，用数值方法计算其收敛阶，定义

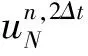
5 结束语

提出了一种求解黏性分数阶MHD方程的数值格式，分析了数值格式的稳定性，得到了格式的误差估计，数值结果验证了格式在时间方向的收敛阶是2-β阶.

表1 不同参数下的时间收敛阶