(2+1)维广义耗散Ablowitz-Kaup-Newell-Segur方程的行波解分岔

周钰谦, 范飞廷, 刘 倩

(1. 电子科技大学 数学科学学院, 四川 成都 611731； 2. 成都信息工程大学 应用数学学院, 四川 成都 610225； 3. 西南民族大学 计算机科学与技术学院, 四川 成都 610041)

在20世纪70年代早期,受非线性光学应用的推动,Ablowitz、Kaup、Newell和Segur在广义Zakharov-Shabat谱问题的基础上推导出了一组Ablowitz-Kaup-Newell-Segur(AKNS)方程[1-4].这组AKNS方程可以简化为一些众所周知的非线性演化方程,如KdV方程、mKdV方程、非线性薛定谔方程和sine-Gordon 方程等,因此它们在物理学和其他非线性科学上有着极其广泛的应用.已经开发了多种方法以获得AKNS方程的显示解,例如逆散射变换[4]、Bäcklund 变换[5]、Darboux变换[6]和Lie群方法[7].

本文考虑如下(2+1)维广义耗散AKNS方程[8]

λuxt+αuxuxy+βuxxuy+

uxxxy+μuxx=0,

(1)

其中λ、α和β均为非零实常数,而系数μ≠0表示系统(1)具有耗散效应[9].事实上,当固定系统(1)中一个或多个系数时,现有文献已经使用了多种方法以获得对应系统行波解的精确表达式,例如改进的tanh法[10]、 简化的Hirota双线性法[11]、修订的扩展同宿测试法(mEHTA)[12]、 二元贝尔多项式法[13]、 扩展的辅助方程法[14]、Hirota双线性法[15]、双线性Bäcklund变换[16]、ansatz 法[17]、(G′/G)扩展法[18]、 简单方程法(SEM)和修正的简单方程法(MSEM)[19].

本文的兴趣在于采用动力系统分岔法获得(2+1)维广义耗散AKNS方程更具一般形式的行波解的精确表达式.所获得的精确解不仅在物理科学中有着非常重要的作用,也有助于进一步了解该模型所描述的物理现象.据查文献,在以前的工作中还没有使用过该方法对系统(1)进行研究.不同于其他的直接方法,动力系统分岔方法可以清楚地解释当参数发生改变时这些解是如何演化的.事实上,这种方法已经被广泛地运用到多种不同的方程中[20-24].

1 (2+1)维广义耗散AKNS方程行波系统的分岔

令u(x,y,t)=u(ξ),ξ=x+ay-ct,系统(1)可化为如下相应的行波系统

(μ-cλ)u″+

(aα+aβ)u′u″+au″″=0,

(2)

其中e是积分常数.令u′=v,则有

(3)

显然(3)式中的第二个式子不含函数u,则可先从(3)式的第二个式子的流形开始分析,进而可将其重写成如下等价的动力系统

(4)

通过计算可得它的能量函数为

(5)

接下来,研究系统(4)的平衡点的分类和性质.

定理 1若α+β≠0,当

(μ-cλ)2+2ae(α+β)>0

时,系统(4)有2个平衡点

为中心，

为鞍点；当

(μ-cλ)2+2ae(α+β)=0

(μ-cλ)2+2ae(α+β)<0

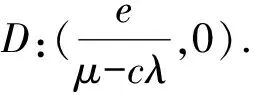
a(μ-cλ)>0

时,B为中心；当

a(μ-cλ)<0

时,B为鞍点.

若α+β=0且μ-cλ=0,当且仅当e=0时系统(4)有且仅有一个退化的平衡点E(0,0),否则没有平衡点.记M(v,y)是系统(4)在点(v,y)处的线性化系统的系数矩阵,则有

于是

根据Hamilton系统的理论[25]可知A是中心,B是鞍点.

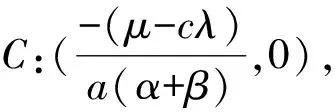
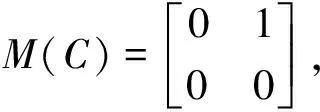
即说明C是一个退化的平衡点.为了进一步判断它的类型,做如下同胚变换

可将系统(4)转化为它的一般形式

根据文献[26]第二章第七节的相关结论可知,此时k=2,bn=0,即说明C是尖点.

当(μ-cλ)2+2ae(α+β)<0时,系统(4)没有平衡点.

类似的分析可用来证明其余2种情况,这里为了简洁,不再赘述.

基于上述对系统(4)的平衡点的分析,得到如下结果：

情形1考虑α+β≠0且

(μ-cλ)2+2ae(α+β)>0.

此时存在一条连接着鞍点B的同宿轨γ,而中心A周围有一簇周期轨

Γ(h)={H(u,y)=h,h∈(Q1,Q2)},

其中

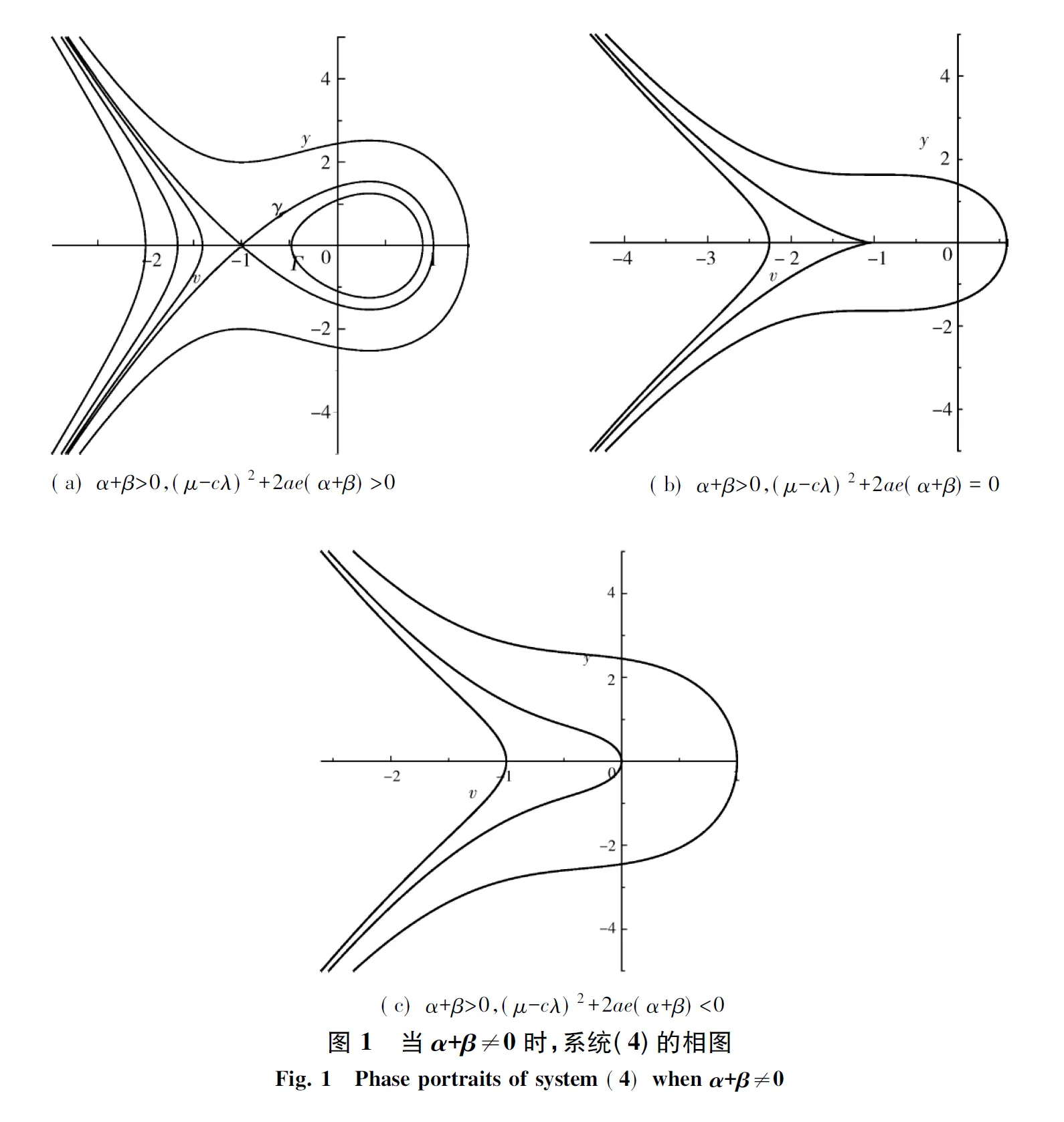
当h→Q1时,Γ(h)趋向于中心A；当h→Q2时,Γ(h)趋向于同宿轨γ,如图1(a).

情形2考虑α+β≠0且

(μ-cλ)2+2ae(α+β)=0,

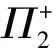
情形3考虑α+β≠0且

(μ-cλ)2+2ae(α+β)<0,

系统(4)只存在无界轨道,如图1(c).

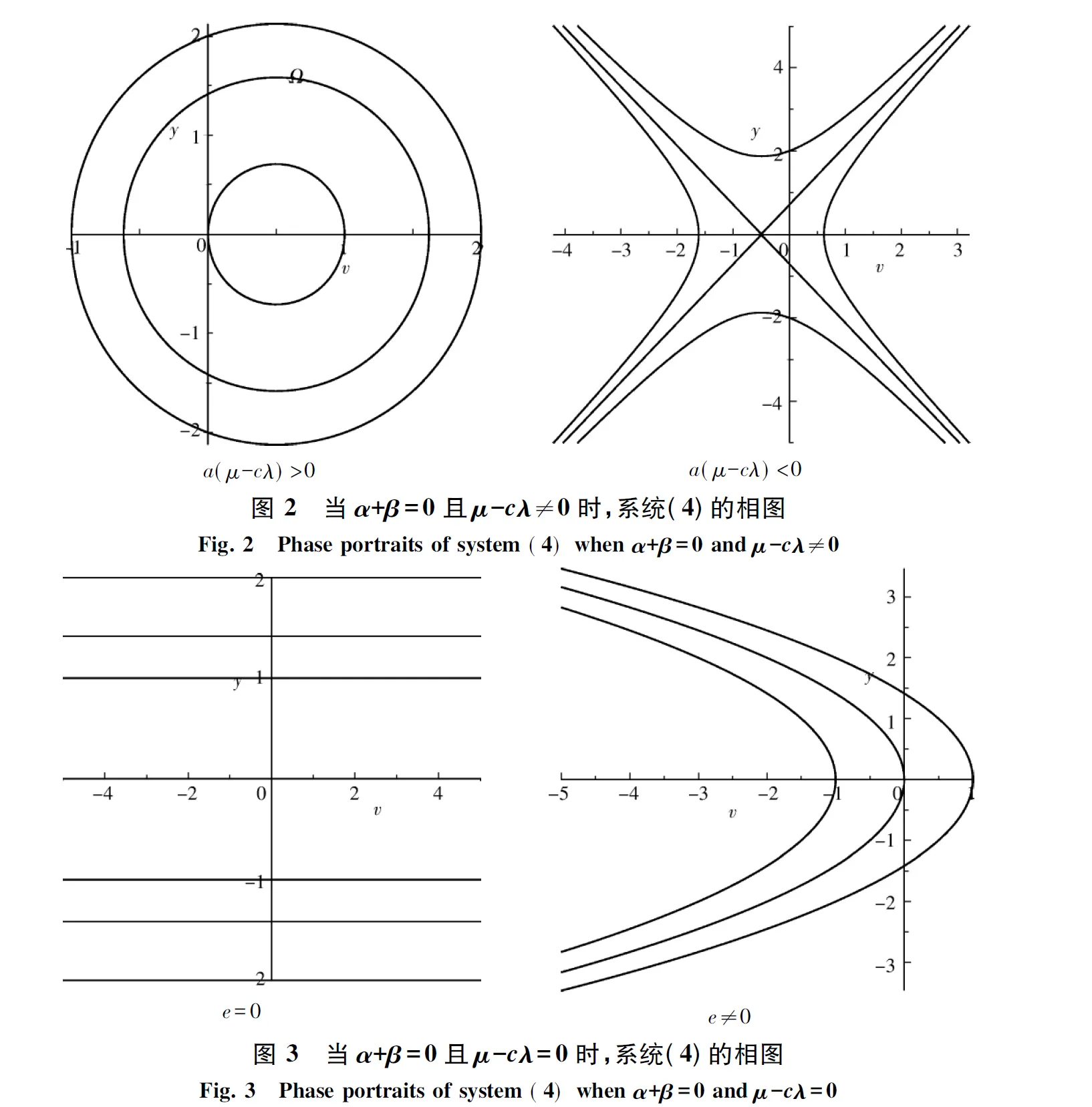
情形4考虑α+β=0且μ-cλ≠0,若

a(μ-cλ)>0,

则系统(4)全是周期轨(如图2(a))；若

a(μ-cλ)<0,

则系统(4)不存在有界轨道,如图2(b).

情形5考虑α+β=0且μ-cλ=0,方程(4)全为无界轨道(如图3).

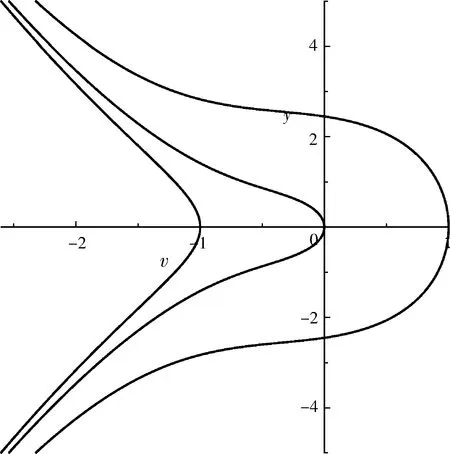
2 (2+1)维广义耗散AKNS方程的精确行波解

根据在第一节中的分析,下面考察系统(4)的所有有界行波,主要存在于情形1(如图1(a))和情形4(如图3(a))中.通过计算椭圆积分,最终给出系统(1)所对应的行波解的精确表达式.

(I) 首先考察情形1中的所有有界轨道,如图1(a)中的轨道γ和Γ,其中γ是系统(4)的同宿轨,Γ是系统(4)中的任一条周期轨.此时α+β>0且(μ-cλ)2+2ae(α+β)>0,则由(5)式可将同宿轨如下表出:

其中

且满足关系r1

通过直接计算可得系统(4)的孤波解为

v1(ξ)=r1+

-∞<ξ<+∞.

注意到,当ξ<0时,

这说明v1(ξ)在ξ<0时和ξ>0时有着相同的表达式,于是可以将v1(ξ)简化成

v1(ξ)=r1+

-∞<ξ<+∞.

进而,可以由(3)式得到系统(1)的第一个精确行波解

u1(ξ)=r1ξ-

-∞<ξ<+∞,

其中C1是积分常数.特别地,当r1=0时,系统(1)的这类行波将退化成扭波.

同理可由(5)式将图1(a)中的任一条闭轨统一表示为

其中实数r3、r4和r5满足关系r3

0<ξ

通过计算复杂的椭圆积分得系统(4)的周期波解

v2(ξ)=r3+

-T<ξ

v2(ξ)=r3+

-T<ξ

于是由(3)式的第一个表达式,系统(1)的第二个行波解的精确表达式为

-T<ξ

此外,当α+β<0且(μ-cλ)2+2ae(α+β)>0时,对系统(4)所对应的有界轨道的讨论类似,为了简洁,这里不再赘述.

(II) 考察情形4中的所有有界轨道,如图2(a),此时α+β=0且a(μ-cλ)>0,行波系统(4)全为周期轨，则其中任一条轨道可被统一表示成

其中实数r6和r7满足关系r6

假设闭轨的周期为2T,并令v(0)=r6,则有

0<ξ

-T<ξ<0.

通过计算得系统(4)的周期波解

v3(ξ)=

-T<ξ

由余弦函数的奇偶性可得

-T<ξ

进而,由(3)式可计算出系统(1)的第三个行波解

其中C2是积分常数.