一类混合变分不等式的可变度量惯性近似点算法
余 静, 夏福全
(四川师范大学 数学科学学院, 四川 成都 610066 )
本文总假设Rn为欧式空间,〈·,·〉和‖·‖ 分别表示Rn的标准内积和l2范数.
设W⊆Rn是非空闭凸子集,θ:Rn→R是下半连续凸函数,F:Rn→Rn是单值映射.本文所研究的混合变分不等式问题(MVIP)为:求w*∈W,使得
θ(w)-θ(w*)+〈w-w*,F(w*)〉≥0,
∀w∈W.
(1)
显然问题(1)等价于:求w*∈W,使得
0∈(F+∂(θ+IW))(w*),
(2)
其中IW表示集合W的指示函数,其定义为
∂f表示函数f:Rn→R的次微分,其定义为:对∀x∈Rn,
∂f(x)={ξ∈Rn|f(y)-f(x)≥
〈ξ,y-x〉,y∈Rn}.
显然,问题(2)是极大单调包含问题的特例.极大单调包含问题即为:求w*∈Rn,使得
0∈T(w*),
(3)
其中T:Rn⟹Rn是极大单调集值映射.对于极大单调包含问题(3),已经有很多的算法,方法之一为经典的近似点算法(PPA).为了获得下一步迭代点wk+1,经典近似点算法需要求解近似子问题
0∈λkT(w)+w-wk,
(4)
其中,wk是当前迭代点,λk是正的参数.对于问题(4),Parente等[1]提出了广义近似子问题
0∈λkMkT(w)+w-wk,
(5)
其中Mk为n阶对称正定矩阵.显然问题(5)等价于
(6)
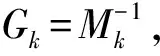
0∈λkT(w)+Gk(w-wk).
(7)
另一方面,Alvarez等[2]研究了极大单调包含问题(3)的惯性近似点算法,迭代如下:任给wk-1,wk∈Rn,参数序列αk∈[0,1],λk>0,求wk+1∈Rn使得
(8)
如果(8)式中的αk≡0,k=0,1,2,…,则以上迭代就退化为经典近似点迭代.如果αk和λk满足一定的条件,并且T-1(0)≠∅,Alvarez等[2]证明了由(8)式产生的迭代序列{wk}收敛于T-1(0)中的点.随后,Alvarez[3]证明了惯性的实施加快了(8)式中迭代序列的收敛速度.
最近,Chen等[4]应用Alvarez等[2]的思想,提出了求解问题(1)的一般惯性近似点算法.算法如下:
设G是n阶半正定对称矩阵,给定参数列
{αk≥0:k=0,1,2,…}, {λk>0:k=0,1,2,…}.
对任给w0=w-1∈Rn,求wk+1∈W,k=0,1,2,…,使得
θ(w)-θ(wk+1)+〈w-wk+1,F(wk+1)+
(9)
(i) 问题(1)的解集W*≠∅;
(ii) 映射F是H-单调,即对∀u,v∈Rn有
其中H是n阶半正定对称矩阵;
(iii)G+H是正定矩阵.
对于假设条件(ii)和(iii),当映射F是单调映射时,即矩阵H≡0时,G为对称正定矩阵.
显然(9)式等价于
(10)
其中T=F+∂(θ+IW).
受到(7)和(10)式的启发,本文将研究一般混合变分不等式问题(1)的变度量惯性算法.具体方法是:在算法中,将近似子问题(10)中的不变矩阵G变为可变对称正定矩阵Gk,获得算法的可变度量惯性近似子问题
(11)
本文在Chen等[4]相似的假设条件下,获得了算法的全局收敛性和收敛率方面的结果.
1 预备知识

设λmin(G)、λmax(G)分别为矩阵G的最小特征值与最大特征值.易知,如果存在λl,λu>0,使得λl≤λmin(G)≤λmax(G)≤λu,则有
(12)
下面给出单调映射的定义以及下半连续函数的定义,定义1.1参见文献[5],定义1.2参见文献[6].
定义 1.1[5]设F:Rn→Rn,如果对任意x,y∈Rn,均有
〈x-y,F(x)-F(y)〉≥0,
则称映射F在Rn上单调.
定义 1.2[6]设f:Rn→R,若对任意收敛于x的点列{xk}⊆Rn均有
则称函数f:Rn→R在x处下半连续.如果函数f在Rn上每一点均下半连续,则称f在Rn上下半连续.
首先证明一些有用的性质.
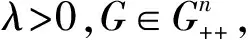
P(·)=(I+λG-1T)-1(·),
则P:Rn→Rn是单值映射且是G范数下的非扩张映射.
证明对∀x∈Rn,若存在z1,z2∈Rn,且z1≠z2,使得
z1=P(x)=(I+λG-1T)-1(x),
z2=P(x)=(I+λG-1T)-1(x).
易知
x∈(I+λG-1T)(z1)=z1+λG-1T(z1),
x∈(I+λG-1T)(z2)=z2+λG-1T(z2).
进而有
λ-1G(x-z1)∈T(z1),
λ-1G(x-z2)∈T(z2).
由T的单调性有
〈λ-1G(x-z1)-
λ-1G(x-z2),z1-z2〉≥0.
(13)
由(13)式可得
〈λ-1G(z2-z1),z1-z2〉≥0.
(14)
由(14)式及λ>0可得
〈G(z1-z2),z1-z2〉≤0.
(15)
下面证明P为G范数下的非扩张映射.对∀x,y∈Rn且u=P(x),v=P(y).下证
‖u-v‖G≤‖x-y‖G.
事实上,由u=P(x),v=P(y)有
x∈(I+λG-1T)(u)=u+λG-1T(u),
y∈(I+λG-1T)(v)=v+λG-1T(v).
从而存在z1∈T(u),z2∈T(v)使得x=u+λG-1z1,y=v+λG-1z2.因此
2λ〈u-v,G-1(z1-z2)〉G=

性质 1.4设W⊆Rn是非空闭凸子集,θ:Rn→R是下半连续凸函数,F:Rn→Rn是单调单值映射,令T(·)=[F+∂(θ+IW)](·),则T-1(0)∩W=W*,其中W*表示问题(1)的解集.
证明显然T:Rn⟹Rn为单调集值映射.对∀w*∈T-1(0)∩W,有0∈T(w*).由T的定义知
0∈F(w*)+∂(φ+IW)(w*).
从而,存在ξ∈∂(φ+IW)(w*),使得0=F(w*)+ξ.根据次微分的定义知ξ满足
(φ+IW)(w)-(φ+IW)(w*)≥〈ξ,w-w*〉,
∀w∈Rn.
(16)
将ξ=-F(w*)代入(16)式可得
(φ+IW)(w)-(φ+IW)(w*)≥
〈-F(w*),w-w*〉, ∀w∈Rn.
(17)
由(17)式及w*∈W可得
φ(w)+IW(w)-φ(w*)≥
〈-F(w*),w-w*〉, ∀w∈Rn.
(18)
由(18)式及对∀w∈W有
φ(w)-φ(w*)≥〈-F(w*),w-w*〉.
(19)
由(19)式可得
φ(w)-φ(w*)+〈w-w*,F(w*)〉≥0.
因此,w*∈W*,故T-1(0)∩W⊆W*.
另一方面,对∀w*∈W*有
φ(w)-φ(w*)+〈w-w*,F(w*)〉≥0,
∀w∈W.
(20)
由(20)式及次微分的定义可得
-F(w*)∈∂(φ+IW)(w*).
(21)
由(21)式可得
0∈F(w*)+∂(φ+IW)(w*),
也即0∈T(w*),因此w*∈T-1(0)∩W,故W*⊆T-1(0)∩W.
2 算法及收敛性
下面给出可变度量惯性近似点算法,并在合适的假设条件下证明算法的序列全局收敛,建立算法的非线性O(1/k)收敛率.

θ(w)-θ(wk+1)+〈w-wk+1,F(wk+1)+
(22)
本文总假设下面的条件成立:
(i)W*≠∅;
(ii)F:Rn→Rn为单调映射;
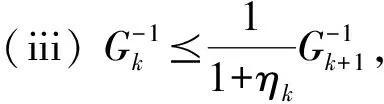
λl≤λmin(Gk)≤λmax(Gk)≤λu.
假设(ii)保证了(22)式中的wk+1是唯一存在的,因此,算法2.1是良定的.下面证明由算法2.1得到的序列全局收敛性.

(23)

证明任取w*∈W*.令
其中T(·)=[F+∂(θ+IW)](·).由性质1.4有w*∈T-1(0),从而
由(22)式及次微分的定义可知
根据上述两式以及Pk的非扩张性可得
2αk〈wk-w*,wk-wk-1〉Gk=
(24)
由假设(iii)可得(1+ηk)Gk+1⪯Gk.因此
(25)
联合不等式(24)和(25)可得
(26)
上式中的第二个不等式是由αk≤ηk获得.由不等式(26)可得
(27)
上式中的等式是由w0=w-1获得,第三个不等式是由(23)式获得.由(12)式及假设条件(iii)可得

联合不等式(27)和(28)可得
(29)
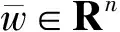

θ(w)-θ(wkj)+〈w-wkj,F(wkj)〉≥
αkj-1(wkj-1-wkj-2)‖Gkj-1≥
-λ-1‖w-wkj‖Gkj-1‖wkj-wkj-1‖Gkj-1-
-λ-1λu‖w-wkj‖‖wkj-wkj-1‖-
(30)
上式中的第三个不等式是由Cauchy-Schwarz不等式获得,第四个不等式是由λk≥λ,αk≤αu获得,最后一个不等式是由(12)式及假设条(iii)获得.由0<αl≤αk可得
再由(23)式可得
因此,根据0<αl≤αk可得
进一步根据(12)式及假设条件(iii)有
因此,(30)式两边同时让j→∞,可得



(31)
即

(32)
显然
(33)
(34)
将(33)和(34)式代入(32)式整理可得
(35)

代入(35)式可得
(1+ηk)φk+1-(1+αk)φk≤
(36)
由1+αk≤1+ηk,αk>0及(36)式可得
(1+αk)(φk+1-φk)≤
(37)
由(37)式可得
φk+1-φk≤
(38)
由0<αl≤αk及(38)式可得
(39)
由(39)式可得
(40)
上式中的第二个不等式是由(23)式获得.由(40)式可得
由(12)式及假设(iii)可得
因此


(b) 对∀w*∈W*,∀k∈N+,有

(41)
证明设w*∈W*,将w=w*代入(22)式,并由F的单调性可得
θ(w*)-θ(wk+1)-〈wk+1-w*,F(wk+1)〉≤
θ(w*)-θ(wk+1)-〈wk+1-w*,F(w*)〉-
〈wk+1-w*,F(wk+1)-F(w*)〉≤0,
即
(42)

〈wk+1-w*,wk+1-wk〉Gk-
αk〈wk+1-w*,wk-wk-1〉Gk≤0.
(43)
显然
(44)
2〈wk+1-w*,wk-wk-1〉Gk=
(45)
将(44)和(45)式代入(43)式整理可得
(46)
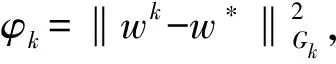
代入(46)式可得
(1+ηk)φk+1-(1+αk)φk≤
(47)
由1+αk≤1+ηk,αk>0及(47)式可得
(1+αk)(φk+1-φk)≤
(48)
由(48)式可得
(49)
上式中的第二个不等式是由Cauchy-Schwarz不等式获得,第三个不等式是由假设(iii)获得,最后一个不等式是由ηk>0获得.
令
由(49)式可得
uk+1-uk=φk+1+
(50)
上式中的第二个不等式是由αk≤αk+1获得,最后一个不等式是由αl≤αk≤αu获得.由(50)式及αu<1/3可知{uk}是非增序列,且uk≥0,k=0,1,2,…,则
(51)
由(51)式可得
u0-uk+1≤φ0,
(52)
上式中的第二个不等式是由w0=w-1获得.由(52)式可得
(53)
由αk≤αu及(53)式可得
故由定理2.2可知结论(a)成立.由(49)式的第一个不等式可得,对∀i≥0有
(54)
由αi≤αu及(54)式可得

由(55)式可得
(56)
由(56)式及
可推得(41)式成立.


θ(w)-θ(wkj)+〈w-wkj,F(wkj)〉≥
αkj-1(wkj-1-wkj-2)‖Gkj-1≥
-λ-1‖w-wkj‖Gkj-1‖wkj-wkj-1‖Gkj-1-
-λ-1λu‖w-wkj‖‖wkj-wkj-1‖-
(57)
上式中的第三个不等式是由Cauchy-Schwarz不等式获得,第四个不等式是由λk≥λ,αk≤αu获得,最后一个不等式是由(12)式及假设条件(iii)获得.由0<αl≤αk可得
再由(23)式可得
因此,根据0<αl≤αk可得
进一步根据(12)式及假设条件(iii)有
因此,(57)式两边同时让j→∞,可得



证明由定理2.2及定理2.4结论显然成立.

