GIac-内射模与GIac-平坦模的环刻画

陈 东

(成都大学 信息科学与工程学院, 四川 成都 610106)

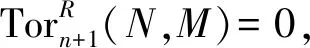
相应地, 环R的GI-整体维数GI-iD(R)以及GI-弱整体维数GI-fD(R)定义为

特别地,Gao[1]证明了R是半单环当且仅当每个R-模是GI-内射模,R是von Neumann正则环当且仅当每个余挠模是GI- 内射模;Gao[2]证明了R是von Neumann正则环当且仅当每个R-模是GI-平坦模.

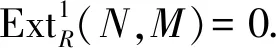
…→E1→E0→E0→E1→…

使得M≅Ker(E0→E0),且对任意的FP-内射模I,函子HomR(I,-)使上述正合列保持正合.

相应地,Zhao等[5]定义了M的DI-内射维数DI-idRM和DI-平坦维数DI-fdRM, 以及环R的DI-整体维数DI-iD(R)和DI-弱整体维数DI-fD(R).作为DI-内射模和DI-平坦模的环刻画,Zhao等[5]也证明了R是半单环当且仅当每个R-模是DI-内射模;R是von Neumann正则环当且仅当每个R-模是DI-平坦模.

受以上思想的启发,本文用 Gorenstein AC-内射模代替Gorenstein内射模,由此引入GIac-内射模和GIac-平坦模的概念.称R-模M是Gorenstein AC-内射模,如果存在内射模的正合列：

…→E1→E0→E0→E1→…,

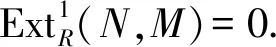
注意,Gao[1]和Zhao等[5]用GI-内射模(或GI-平坦模)和DI-内射模(或DI-平坦模)分别刻画了半单环、von Neumann正则环、遗传环和半遗传环.一个自然的问题是,能否也用GIac-内射模和GIac-平坦模刻画上述环类？本文肯定的回答了这个问题,证明了每个R-模是GIac-内射模当且仅当R是半单环,每个R-模是GIac-平坦模当且仅当R是von Neumann正则环.相应地,定义R-模M的GIac-内射维数和GIac-平坦维数,及环R的GIac-整体维数GIac-iD(R)及GIac-弱整体维数GIac-fD(R).证明了R是遗传环当且仅当GIac-iD(R)≤1,且每个GIac-内射模是内射模;R是凝聚环,则R是半遗传环当且仅当GIac-fD(R)≤1,且每个GIac-平坦模是平坦模.

为方便讨论,需回顾相关概念：

…→F1→F0→F0→F1→…

使得M≅Ker(F0→F0),且对任意的绝对clean模I,函子I⊗-使上述正合列保持正合.相关概念,参见文献[6-14],不再赘述.

本文所涉及的环均是有单位元的交换的结合环,所涉及的模均是酉模.用D(R) 表示环R的整体维数,wD(R)表示环R的弱整体维数,M+表示模M的特征模 Homz(M,Q/Z).设是L模类,用⊥L和L⊥分别表示L的左、右正交类.

1 主要结果

首先引入GIac-内射模和GIac-平坦模的概念,可以看到GIac-内射模是介于GI-内射模与余纯内射模之间的一个模类,GIac-平坦模是介于GI-平坦模与余纯平坦模之间的一个模类.

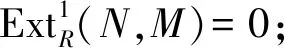
注11) 由文献[9]中的定义知, {Gorenstein AC-内射模}⊆{Gorenstein 内射模},于是存在以下包含关系：

{内射模}⊆{GI-内射模}⊆{GIac-内射模} ⊆{余纯内射模}

{平坦模}⊆{GI-平坦模}⊆{GIac-平坦模}⊆{余纯平坦模}

2) 若R是Noether 环,则Gorenstein内射模就是Gorenstein AC-内射模,此时{GI-内射模}={GIac-内射模};若D(R)<∞,则Gorenstein AC-内射模是内射模,此时 {GIac-内射模}={余纯内射模}.

3) 若R是凝聚环,则FP-内射模等价于绝对clean模.此时,Gorenstein平坦模就是 Gorenstein AC-平坦模.

4) 若R既是Noether环,又是完全环,则投射模等价于level模.此时,Gorenstein投射模就是Gorenstein AC-投射模.

现举一个余纯内射模,但不是GIac-内射模的例子.

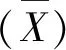
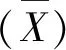
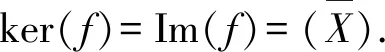
命题1设M是R-模,以下各条等价：

1)M是GIac-内射模;

2) 对正合列0→M→E→L→0,其中E是Gorenstein AC-内射模,则E→L是L的Gorenstein AC-内射预覆盖;

3) 同态：E(M)→E(M)/M是E(M)/M的Gorenstein AC-内射预覆盖,其中E(M)表示M的内射包络;

4)M是某个R-模B的Gorenstein AC-内射预覆盖g:A→B的核,其中A是内射模;

5) 对正合列0→A→B→C→0,其中C是Gorenstein AC-内射模,函子HomR(-,M)使该正合列保持正合.

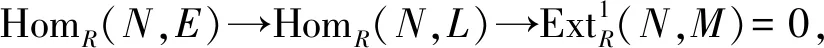
2)⟹3) 由于0→M→E(M)→E(M)/M→0是正合列,其中E(M)表示M的内射包络,故也是Gorenstein AC-内射模.由2)知,E(M)→E(M)/M是E(M)/M的Gorenstein AC-内射预覆盖;

3)⟹4) 显然;

1)⟹5) 显然;

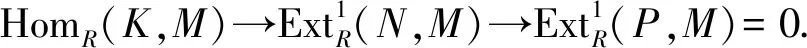
命题2设M是R-模,以下各条等价:

1)M是GIac- 平坦模;

2)M=⊥,其中={B+|B是GIac-内射模};

3) 对正合列0→A→B→C→0,其中C是Gorenstein AC-内射模,函子M⊗-使该正合列保持正合.

命题31) 设R是环,M是GIac-内射模.若M的Gorenstein AC-内射维数小于等于1,则M是内射模;

2) 设R是环,M是GIac-平坦模.若M的Gorenstein AC-平坦维数小于等于1,则M是平坦模.

2) 设M是GIac-平坦模,则M+是GIac-内射模,于是有M+的Gorenstein AC-内射维数小于等于1.由1)知,M+是内射模,故M是平坦模.

定理1设R是环,以下各条等价：

1) 每个R-模是GIac-内射模;

2) 每个R-模是强GIac-内射模;

3) 每个Gorenstein AC-内射模是投射模;

4) 每个Gorenstein AC-投射模是内射模;

5)R是半单环.

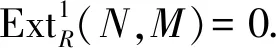
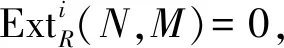
2)⟹1) 显然.

4)⟹5) 设M是投射模,由定义知,M也是Gorenstein AC-投射模.由4)知,M是内射模,故R是QF环,于是每个R-模N都是Gorenstein投射模.注意此时R是QF环,故由注1知,Gorenstein投射模等价于Gorenstein AC-投射模,再由4)知,N是内射模.因此,R是半单环.

5)⟹4) 显然.

3)⟹5) 设M是内射模,N是任意的R-模.由定义1知,M也是Gorenstein AC-内射模.由3)知,M是投射模,故R是QF环,于是每个R-模N是Gorenstein内射模.注意此时R是Noether环,故由注1知,Gorenstein内射模等价于Gorenstein AC-内射模,于是又由3)知,N是Gorenstein AC-内射模,从而也是投射模.因此,R是半单环.

5)⟹3) 显然.

称环R是von Neumann正则环,是指每个R-模是平坦模或FP-内射模;环R是IF环, 是指每个内射模是平坦模.Ding等[16]证明了IF环就是FC 环.环R是FC环,是指R是自FP-内射的凝聚环.下面用GIac-平坦模刻画von Neumann正则环：

定理2设R是环,以下各条等价：

1) 每个R-模是GIac-平坦模;

2) 每个R-模是强GIac-平坦模;

3) 每个Gorenstein AC-内射模是平坦模;

4) 每个余挠模是GIac-内射模;

5) 每个纯内射模是GIac-内射模;

6)R是von Neumann 正则环.

证明1)⟹2) 由注1及定理1.

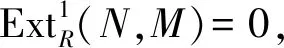
4)⟹5) 由于每个纯内射模是余挠模,故5)成立.

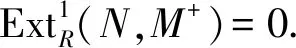
2)⟹1) 显然.

3)⟹6) 设E是内射模,由定义1知,E也是Gorenstein AC-内射模.由3)知,E是平坦模,故R是IF环,从而是FC环,于是每个R-模M是Gorenstein-平坦模.注意此时R是凝聚环,故由注1知,M也是Gorenstein AC平坦模,从而有M+是Gorenstein AC-内射模.再由3)知,M+是平坦模,故M是FP-内射模.因此,R是von Neumann正则环.

6)⟹1) 由于每个平坦模是GIac-平坦模, 故1)成立.

模的GI-内射维数、DI-内射维数、GI-平坦维数和DI-平坦维数的定义分别见文献[3-5].类似地,现定义模的GIac-内射维数和GIac-平坦维数：

定义2设M是R-模：

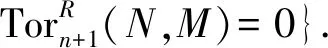
相应地,环R的GIac-整体维数GIac-iD(R)以及GIac-弱整体维数GIac-fD(R)定义为

3)GIac-iD(R)=sup{GIac-idRM|M是任意的R-模};

4)GIac-fD(R)=sup{GIac-fdRM|M是任意的R-模}.

注2由上述定理容易看到,环R的GIac-整体维数刻画了环R与半单环的距离,即GIac-iD(R)=0当且仅当R是半单环;环R的GIac-弱整体维数刻画了环R与von Neumann正则环的距离,即GIac-fD(R)=0当且仅当R是 von Neumann 正则环.

命题4设M是R-模,若idRM<∞则Gac-idRM=idRM.因此,当D(R)<∞时,GIac-iD(R)=D(R).

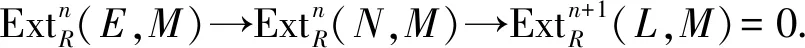
定理3设R是环,以下各条等价：

1)GIac-iD(R)≤1;

2) Gorenstein AC-内射模的投射维数小于等于1;

3) 强GIac-内射模的商模是强GIac-内射模;

4) 内射模的商模是强GIac-内射模;

5)GIac-内射模的商模是GIac-内射模;

6) 内射模的商模是GIac-内射模.

3)⟹4) 显然.

4)⟹3) 设M是强GIac-内射模,L是M的商模,于是存在正合列： 0→K→M→L→0.另一方面,又存在正合列：0→K→E→C→0,其中E是内射模.于是存在以下正合列的交换图如图1所示.

图1 交换图Fig.1 Commutative diagram

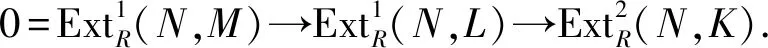
5)⟹6) 显然.

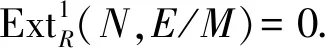
环R称为遗传环,是指D(R)≤1;环R称为半遗传环,是指R是凝聚环,且wD(R)≤1.现用环R的GIac-内射维数刻画遗传环：

定理4环R是遗传环当且仅当GIac-iD(R)≤1,且每个GIac-内射模是内射模.

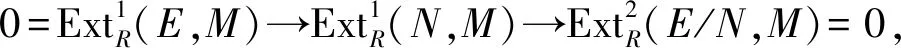
⟸ 设M是任意的R-模,故存在正合列： 0→N→E→E/N→0,其中E是内射模.由于E也是GIac-内射模,且GIac-iD(R)≤1,故E/N也是GIac-内射模.由题意知,E/N是内射模,故D(R)≤1,从而R是遗传环.

最后,用环R的GIac- 平坦维数刻画半遗传环：

定理5设R是凝聚环,则R是半遗传环当且仅当GIac-fD(R)≤1,且每个GIac-平坦模是平坦模.

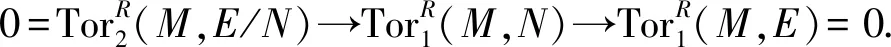
⟸ 设M是任意的R-模,故存在正合列： 0→K→F→M→0,其中F是平坦模.由于F也是GIac-平坦模,且GIac-fD(R)≤1,故K也是GIac-平坦模,由题意知,K是平坦模,故wD(R)≤1,从而R是半遗传环.