基于拉普拉斯度的k-均匀超图的图熵极值
卢鹏丽, 薛玉龙
(兰州理工大学 计算机与通信学院, 甘肃 兰州 730050)
设H=(V(H ),E(H ))是一个顶点数为n,超边数为m的超图.其中顶点集V(H )={1,2,…,n},超边集E(H )={e1,e2,…,em}(不包括空集).和图相比较,超图的每条超边上可以有多个顶点.若超图的所有超边都有相同的顶点个数k,则称之为k-均匀超图.显而易见,通常意义上的图就是2-均匀超图.因此,图是一种特殊的超图,超图也可以看成是一般图的推广.因此,超图的一些性质与图的性质相似,但是又有所不同.通常情况下为了叙述简便,一般也将超边简称为边.没有重边的k-均匀超图被称为简单k-均匀超图.在超图中长度为r的途径W用一个顶点和边交替的序列v0e1v1e2…ervr来表示,其中{vi-1,vi}⊆ei,i=1,…,r.若回路中除v0=vr外,没有其他顶点或者边重复,则这个回路被称为圈.若v0=vr,则称途径W为一个回路.若途径W中没有顶点或者边重复,则称这条途径W为超路Pn.若超图中任意两个顶点之间有途径连接,则该超图被称为是连通的.本文中,只考虑简单连通的k-均匀(k≥3)超图.
在超图中,若顶点v∈e,则称顶点v和边e相关联.若存在一条边包含顶点vi和vj,则称顶点vi和vj相邻接.若两条边的交集ei∩ej≠∅,则表示这两条边vi和vj相邻.对于k-均匀超图H,包含顶点v∈V(H )的边的个数定义为顶点v的度,即dv=|ej:v∈ej∈E(H )|.度d=1的顶点称为悬挂点,否则被称为非悬挂点.若边e∈E(H)正好包含k-1个悬挂点,则称e为悬挂边,否则被称为非悬挂边.
定义1[1]设H是一个顶点数为n,边数为m,连通分支数为l的k-均匀超图.则H的圈数为c(H )=m(k-1)-n+l.因此,超图H可以称为c(H )圈超图.
由于本文中只考虑简单连通超图,所以c(H)=m(k-1)-n+1.
定义2[2]超树是连通、无圈的超图.
定义3[2-3]树的k次幂称为k-均匀超树.
超树(hypertree)的每条边上最多有两个非悬挂点,本文讨论的超树均是hypertree.与化学树的定义类似,定义化学超树是最大度不超过4的超树.
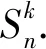
定义5[4]设G是一个顶点集V(G)={v1,v2,…,vn}的连通图,其中顶点vi的度为di.则基于度的图熵定义为
早在1949年,Shannon等[5]为了解决通信中信息量化的问题提出Shannon熵.受此启发,Dehmer[6]将Shannon熵的概念引入图论中,用来描述图的结构信息,简称为图熵. Cao等[4]基于图熵的定义提出了基于度的图熵,确定了一些图类的图熵极值,并找到了图熵与度幂之和的关系.Das等[7]得到了基于度幂的图熵的一些上界和下界,并刻画了极值图.Hu等[8]确定了基于度的一些特定均匀超图的图熵的极值.关于图熵的研究还有很多,详见文献[9-12].
1 基本理论

设π(H)=(δ1,δ2,…,δn)为超图H的非增拉普拉斯度序列,其中δ1≥δ2≥…δn,则
根据定义5,定义超图中基于拉普拉斯度的图熵为
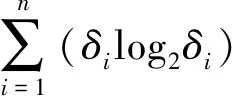
定义7[2]设超图H=(V(H),E(H))中顶点u∈V(H),边e1,…,er∈E(H),其中r≥1,u∉ei(i=1,…,r).令顶点vi∈ei,边e′i=(ei﹨{vi}∪{u}),其中i=1,…,r.设超图H′=(V(H),E′(H))的边集E′(H)=(E(H)﹨{e1,…,er})∪{e′1,…,e′r}.因此,通过分别移动超图H边(e1,…,er)上的顶点(v1,…,vr)到顶点u可得到超图H′.
引理1设超图H上存在两个顶点vi和vj使得拉普拉斯度δi≥δj+2(k-1),其中顶点vi∈e∈E(H ),顶点vj∉e.若超图H通过定义7的移边操作,移动边e上的顶点vi到顶点vj可得到超图H′,则h(H)>h(H′).
证明由于δi≥δj+2(k-1),因此δi>δi-(k-1)≥δj+(k-1)>δj.则
其中ξ1∈(δi-(k-1),δi),ξ2∈(δj,δj+(k-1)).
证毕.
引理2设超图H上存在两个顶点vi和vj使得拉普拉斯度δi≥δj≥2(k-1),其中顶点vj∈e∈E(H),顶点vi∉e.若超图H通过定义7的移边操作,移动边e上的顶点vj到vi可得到超图H′,则h(H) 证明由于δi≥δj≥2(k-1),因此δi+(k-1)>δi≥δj>δj-(k-1).则 h(H)-h(H′)=δilog2δi+δjlog2δj- (δi+(k-1))log2(δi+(k-1))- (δj-(k-1))log2(δj-(k-1))= -{(δi+(k-1))log2(δi+(k-1))- δilog2δi}+{δjlog2δj- (δj-(k-1))log2(δj-(k-1))}= -(k-1)(log2ξ1-log2ξ2)<0 其中:ξ1∈(δi,δi+k-1),ξ2∈(δj-(k-1),δj). 证毕 引理3[2]设H ′是单圈k-均匀超图H经过移边操作后得到的超图.若H ′是连通的,则H ′仍然是单圈k-均匀超图. 引理4[2]设H ′是双圈k-均匀超图H经过移边操作后得到的超图.若H ′是连通的,则H ′仍然是双圈k-均匀超图. 因此,单圈k-均匀超图经过定义7中的移边操作之后仍然是单圈k-均匀超图.双圈k-均匀超图经过定义7中的移边操作之后仍然是双圈k-均匀超图. 引理5[14]设f为定义在实数集R上的严格凸函数,x,y∈Rn,则 证毕 设H*是拉普拉斯度序列π(H*)=[2k-2(m),k-1(n-m)]的单圈k-均匀超图.H**是拉普拉斯度序列π(H**)=[2k-3(2),k-1(n-2)]的单圈k-均匀超图. 当且仅当H ≅H**时,左侧等式成立.当且仅当H ≅H*时,右侧等式成立. 证明设f(x)=xlog2x,其中x≥0.由于f(x)是严格凸函数,因此h(H )满足引理5中的结论.非增拉普拉斯度序列π(H )=(δ1,δ2,…,δn)中的前r项越大,则h(H )越大.反之,则结论相反.换而言之,由于拉普拉斯度之和为k(k-1)m,且连通图中拉普拉斯度最小为k-1,因此拉普拉斯度序列中k-1的个数越多,则h(H )越大. 单圈k-均匀超图可以分为以下三种结构:多悬挂边,单悬挂边,无悬挂边.不难得出,有悬挂边结构的单圈k-均匀超图最大的拉普拉斯度δ1>2(k-1),而无悬挂边结构时δ1=2(k-1).根据引理5,可得单圈k-均匀超图是无悬挂边结构时,h(H)取到最小值,即h(H)≥h(H*).无悬挂边结构的单圈k-均匀超图的拉普拉斯度序列π(H*)=[2k-2(m),k-1(n-m)].因此 当圈上包含的边数相同时,多悬挂边结构的拉普拉斯度为k-1的顶点个数比单悬挂边结构的多.因此,只需考虑多悬挂边结构的特殊情况,拉普拉斯度为k-1的顶点个数最多时,h(H )取最大值.多悬挂边结构的单圈k-均匀超图中最多有n-2个顶点的拉普拉斯度为k-1,其拉普拉斯度序列π(H**)=[2k-3(2),k-1(n-2)].因此 由上述讨论,可得 {2m(k-1)log2[2(k-1)]+ (n-m)(k-1)log2(k-1)} 证毕 设H*是拉普拉斯度序列π(H*)=[2k-2(m+1),k-1(n-m-1)]的双圈k-均匀超图.H**是拉普拉斯度序列π(H**)=[mk-m,2k-3(2),k-1(n-3)]的双圈k-均匀超图. 证明使用反证法证明.设HH*获得最小的基于拉普拉斯度的图熵.则至少存在一个顶点u满足δu≥3k-3.令e为包含顶点u的非悬挂边,C=v1e1v2e2…etvt+1(vt+1=v1)是H中的一个圈.而满足条件的顶点u有以下两种情况. 情况1:顶点u在圈C中,即u∈C. 不失一般性,设边e=e1,顶点u∈e1.找一条从顶点u开始最长的超路P=uf1u1f2…fsus,其中顶点ui∉C且边fi∉C(i=1,2,…,s).显然,顶点us的拉普拉斯度δus=k-1. 若顶点u=v1或者v2.不失一般性,设顶点u=v1,则拉普拉斯度δv1≥3.令H′=(V(H),E(H′))为边集E(H′)=(E(H)﹨{e1})∪{e′1}的双圈k-均匀(k≥3)超图,其中边e′1=(e1﹨{v1})∪{us}.根据引理1,可得h(H)>h(H′),矛盾. 若顶点u≠v1,v2.设f1是一条不包含顶点u的边,其中f1≠e1.令H ′=(V(H ),E(H ′))为边集E(H ′)=(E(H )﹨{e1,f1})∪{e′1,f′1}的超图,其中边e′1=(e1﹨{v1})∪{us},f′1=(f1﹨{u})∪{v1}.根据引理1,可得h(H )>h(H ′),矛盾. 情况2:顶点u不在圈C中,即u∉C. 找一条从顶点u开始最长超路P=vf1u1f2…fsus(顶点ui∉C,边fi∉C,i=1,2,…,s),其中顶点v∈ei,i∈{1,2,…,t},边fj-1∩fj={u},j∈{1,2,…,s}.令H′=(V(H),E(H′))为边集E(H′)=(E(H)﹨{e1,fj})∪{e′1,f′j}的双圈k-均匀(k≥3)超图,其中边e′1=(e1﹨{vi})∪{us},边f′j=(fj﹨{u})∪{vi}.根据引理1,可得h(H)>h(H′),矛盾. 由上述讨论可得,当且仅当H ≅H*时,h(H)取到最小值,即 h(H )≥(m+1)(2k-2)log2(2k-2)+ (n-m-1)(k-1)log2(k-1) 设H ≅H**获得最大的基于拉普拉斯度的图熵,令u是拉普拉斯度最大的顶点.而顶点u有以下3种情况. 情况1:若边e∈E(H )有k-1个悬挂点,则顶点u∈e. 相反的,设e∈E(H )有k-1个悬挂点,但顶点u∉e.令w∈e是拉普拉斯度δw≥2(k-1)的顶点.令H ′=(V(H ),E(H ′))为边集E(H′)=(E(H )﹨{e})∪{e′}的双圈k-均匀(k≥3)超图,其中边e′=(e﹨{w})∪{u}.根据引理2,得h(H ) 情况2:u是H中所有圈的一个公共点. 相反的,设H中的圈C=v1e1v2e2…etvt+1(vt+1=v1)不包含顶点u.找一条从顶点v开始的超路P=vf1u1f2…us-1fsu(顶点ui∉C,i=1,2,…,s-1,边fj∉C,j=1,2,…,s),其中顶点v∈ei,i∈{1,2,…,t}.令H ′=(V(H ),E(H ′))为边集E(H ′)=(E(H )﹨{ei,f1})∪{e′i,f′1}的双圈k-均匀(k≥3)超图,其中边e′i=(ei﹨{vi})∪{u},边f′1=(f1﹨{v})∪{vi}.根据引理2,可得h(H ) 情况3:对任意在H中的圈C,都有构成圈C的边数|e(C)|=2,其中e(C)={e|e∈C}. 用C=v1e1v2e2…etvt+1(vt+1=v1)表示H中的一个圈.不失一般性,设顶点v2≠u∈e1(u和v1不是同一个顶点).若构成圈C的边数|e(C)|≥3,则令H′=(V(H),E(H′))为边集E(H′)=(E(H)﹨{e2})∪{e′2}的双圈k-均匀(k≥3)超图,其中e′2=(e2﹨{v2})∪{u}.根据引理2,可得h(H ) 由上述讨论可得,当且仅当H≅H**时,h(H)取到最大值,即h(H )≤(mk-k)log2(mk-k)+(4k-6)log2(2k-3)+(n-3)(k-1)log2(k-1). 证毕 根据引理6对双圈k-均匀(k≥3)超图的h(H)的讨论,可得如下结论. 当且仅当H ≅H**时,左侧等式成立.当且仅当H ≅ H*,右侧等式成立. 设T*是顶点数为n,边数为m=3a+i+1(i=0,1,2),拉普拉斯度序列为π(T*)=[4k-4(a),(i+1)(k-1),k-1(n-a-1)]的k-均匀化学超树. 证明h(T)满足引理5中的结论.因此,拉普拉斯度为k-1的顶点个数越多,则h(T)越大.拉普拉斯度序列的前r项越大,则h(T)越大.化学超树的最大度不超过4,即拉普拉斯度最大为4k-4.若存在一对顶点vi和vj,其拉普拉斯度分别是δi和δj,使4(k-1)>δi≥δj≥2(k-1).通过引理2中的移边操作,顶点vi和vj的拉普拉斯度分别变为δi+(k-1)和δj-(k-1),得到了一个新的化学超树T′.根据引理2,可以证明h(T) 因此 1) 若m-1≡0(mod 3),则 2) 若m-1≡0(mod 3),则 3) 若m-1≡0(mod 3),则 证毕 当且仅当T∈T*时,左侧等式成立.当且仅当T ≅Pn时,右侧等式成立. 证明注意到超路Pn也是化学超树.根据定理1,可得化学超树T ≅Pn时,Iδ(T )取到最大值.因此 证毕 本文将简单图的一些结果推广到k-均匀超图.利用超图拉普拉斯度的性质,通过移边操作,分别得到了在k-均匀超树、单圈k-均匀超图、双圈k-均匀超图以及k-均匀化学超树中基于拉普拉斯度的图熵极值,并确定了极值图.在接下来的工作中,还可以将上述结论推广到n圈k-均匀超图,但由于n圈k-均匀超图中存在许多复杂的结构,所以拉普拉斯度序列将是非常多变的,这是研究中的一个难点.
2 基于拉普拉斯度的图熵上、下界与极值图
2.1 k-均匀超树
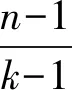


2.2 单圈k-均匀超图
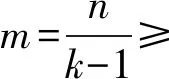
2.3 双圈k-均匀超图

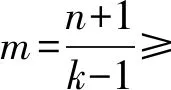
2.4 k-均匀化学超树



3 结论

