一类受到未知外部干扰的多智能体系统学习协同控制

杨娜娜, 孟新友, 玄海燕

(1. 兰州理工大学 理学院, 甘肃 兰州 730050; 2. 兰州理工大学 经济管理学院, 甘肃 兰州 730050)

多智能体系统(MASs)协同控制因其广泛的应用背景,如无人机编队、航天器飞行、传感器网络等,受到多学科专家们的极大关注[1-2].一致性问题作为MASs协同问题研究中最基本且重要的课题,是指在分布式控制协议下,智能体的状态或输出通过与其邻居共享信息而达到一个共同值[3-4],包括带头节点一致性[5-7]和无头节点一致性[8-10],现如今已成为MASs领域的一个研究热点.

此外,实际中,存在大量的系统是可重复运行的[11].在这样的实际背景下,迭代学习控制(ILC) 方法作为一种智能控制算法被提出[12-13].ILC 可以有效解决有限时间区间上可重复运行系统的高精度轨迹跟踪问题,具有控制算法简单、不需要知道具体的数学模型等优点.目前,随着对ILC的深入研究,已经与一些先进控制相结合,产生了诸多新型的控制算法,如自适应控制[14]、模糊控制[15]、最优控制[16]等.

值得一提的是,许建新等[12-16]都是将ILC方法用于单个系统的研究,而近些年来,很多学者[17-22]已将ILC用于MASs 协同问题的研究,其中文献[17～20]利用自适应ILC 的方法分别研究了一阶、二阶和高阶非线性MASs的协同控制问题；Meng等[21]将ILC与输出反馈方法相结合,处理了高阶非线性MASs的有限时间一致性问题；Yang等[22]提出了最优控制器增益的设计方法,使得一致性误差的λ-范数以最快的速度收敛,但这些文献[17-22]都没有考虑到未知外部干扰的影响.实际工程中,由于复杂环境等因素,系统的外部干扰是比较常见的,会对系统的稳定产生一定影响,有时可能导致系统不稳定.因此,在系统的控制器设计时,有必要考虑外部干扰,且具有一定的实际意义.

因此,本文在一类MASs中考虑未知外部干扰,并通过坐标变换,将一致性问题推广到编队问题,解决了区间[0,T]上的完全一致性和编队问题,即MASs 的协同控制问题.

1 问题描述

在重复环境下,考虑一类 MASs:

(1)

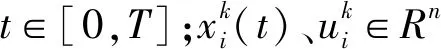
假设2所有的智能体满足对接条件,即:

定义第i个从节点与头节点之间的一致性误差向量为

(2)

再定义第i个从节点的分布式误差向量为

(3)

且由误差(2，3),得：

(4)

ek=-((L+B)⊗In)(xk-1N⊗x0)=

-(H⊗In)δk

其中：

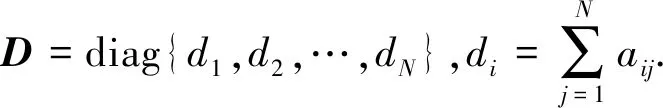
另外,由误差(2),得误差动态为

(5)

2 控制协议设计

基于以上的误差动态(5),设计第i个从节点的分布式控制协议为

其中:Q是任意正定矩阵.

此时,误差动态(5)可集中写为

(8)

其中:

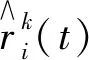
(9)

(10)

其中:

3 学习一致性分析

定理1对于具有通信拓扑图G′的MASs (1), 当假设1、2成立时,设计的控制协议(6,7)以及参数自适应律(9,10)能够使得所有从节点在区间[0,T]上随着迭代次数的无限增加与头节点达到完全一致,即

同时,闭环系统内的所有信号有界.

证明构造如下的复合能量函数(CEF):

(11)

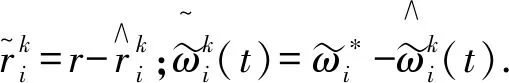
(1) 考查Ek(t)第k次和k-1次之间的差分:

(12)

其中,由式(8，12)中的第1项可变形为

(13)

再由式(9),第3项变形为

(14)

由式(10),第5项变为

(15)

再将式(13～15)代入式(12),得:

(16)

其中:λmin(H)和λmin(Q)是正定矩阵H和Q的最小特征值.

又因为

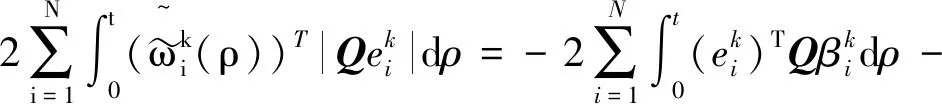
2NTεΔk+1

(17)

其中最后一个不等式由文献[21]中的Lemma 2.2 得到.因此:

(18)

此时,可以选择充分大的r>0, 使得

(QA+ATQ)-2rλmin(H)λmin(Q)I≤-σI

(19)

对于σ>0总成立.从而有

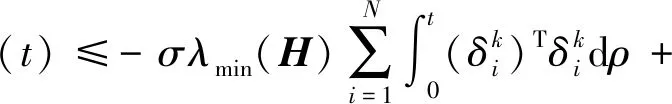
(δk(0))T(H⊗Q)δk(0)-

(δk-1(t))T(H⊗Q)δk-1(t)+

(20)

令t=T,则由假设2和自适应律(9,10)可知:

(21)

即

Ek(T)≤Ek-1(T)+2NTεΔk+1

(22)

(2) 证明闭环系统所有信号的有界性.

由式(12),可得:

Ek(t)=ΔEk(t)+Ek-1(t)≤

(δk(0))T(H⊗Q)δk(0)-

(δk-1(t))T(H⊗Q)δk-1(t)+

Ek-1(T)+2NTεΔk+1

(23)

则

Ek(t)≤Ek-1(T)+2NTεΔk+1

(24)

且

(25)

另外,由文献[21]中的Lemma 2.1：

Ek(t)≤E0(T)+K

(26)

从式(26)可以看到,如果E0(T)有界,就能保证Ek(t)是一致有界的.所以,下面证明E0(t)的有界性.因为

(27)

对式(27)两端求导,得

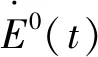
(28)

其中：

2NTεΔ1=2Nεa

(29)

则

(30)

所以:

(31)

(3) 证明[0,T]上的完全一致性.

从式(21),可得:

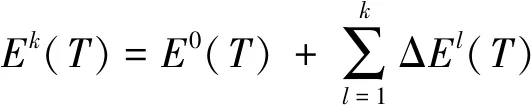
(32)

则

(33)

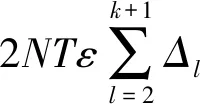
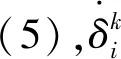
综上,定理1得证.

4 编队问题

对于∀t∈[0,T],若每个从节点与头节点之间能够形成期望的距离,这意味着MASs(1)实现了编队控制.

定义:

(34)

其中：Δi是第i个从节点与头节点之间期望的距离.

第i个从节点与头节点之间的编队误差为

(35)

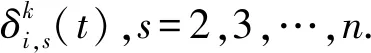
此外,第i个从节点的分布式编队误差定义为

(36)

假设3假设所有智能体满足对接条件,即

(i=1,2,…,N;s=2,3,…,n)

且x0(0)=x0(T).

5 仿真

为了验证本文算法的有效性和实用性,给出一个网络化LC振荡器系统[24],此系统可以看作是一个MASs,由5个从振荡器和1个头振荡器组成,其网络通信拓扑图如图1所示.

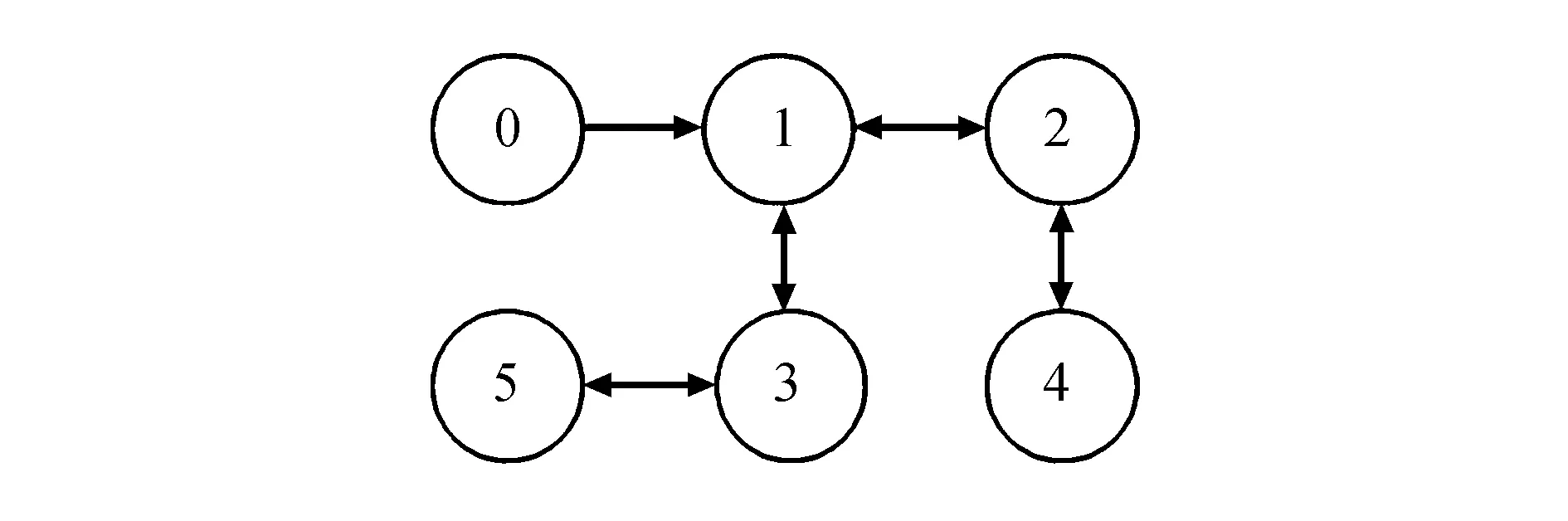
图1 通信拓扑图(0表示头节点)Fig.1 Communication topology graph(0 denotes the leader)

由图1得到,只有第1个从节点可以得到头节点的信息,且L和B分别为

第i个振荡器的动态描述为

(37)

其中:i=1,2,…,6;ci(t)、vi(t)、L′和C分别是电流、电压、电感和电容.

(38)

其中：

h1、h2、l1和l2是[0,1]上的随机数,t∈[0,2].

另外,x0(t)=[sin(πt),cos(πt)]T,满足假设2.

对于MASs(38),运用本文所设计的协议(6，7) 和自适应律(10，11).

情形1：完全一致性问题.

经过40次迭代的仿真结果如图2和图3所示.图2是智能体第40次迭代的状态轨迹图,可以看到所有从节点的状态向量与头节点的状态向量在[0,2]上完全重合.图3是一致性误差沿迭代轴的演化曲线图,显示所有从节点与头节点的一致性误差是一致趋于零的.故图2和图3都说明,在区间[0,2]上,所有从节点随着迭代次数的无限增加,能够完全跟踪上头节点,实现了完全一致性.图4表明,闭环系统的其他变量都有界,进而验证了定理1的成立.

图2 第40次迭代的状态轨迹Fig.2 State trajectories the 40th iteration

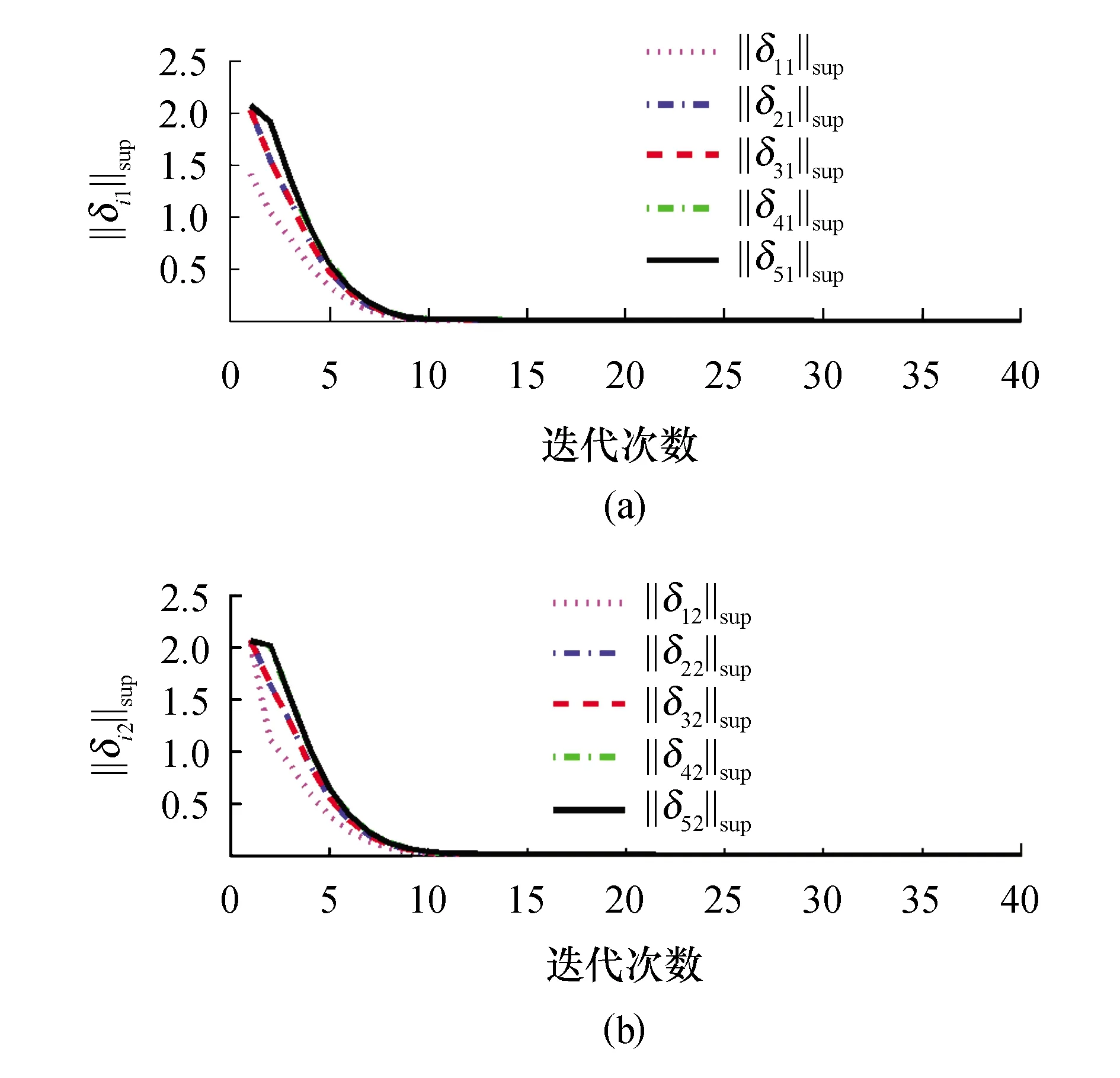
图3 一致性误差沿迭代轴的演化曲线

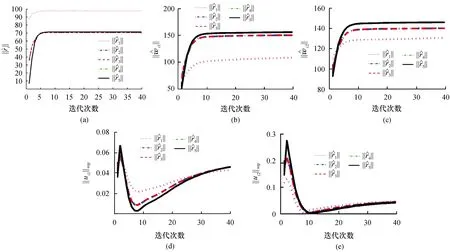
图4 其他变量沿迭代轴的演化曲线Fig.4 Evolution curves of other variables along the iteration axis

iterative axis

情形2：编队问题.

迭代75次仿真结果如图5 所示,可以看出，智能体的状态向量形成了期望的编队.

图5 情形2的仿真结果

6 结论

本文旨在解决一类MASs的学习协同控制问题,其中MASs受到外部时变有界干扰.通过设计具有微分型参数自适应律的时变增益,避免了控制增益对通信拓扑的依赖,同时,设计的辅助控制协议,补偿了从节点动态中的外部干扰.最终,实现了有限时间区间上的完全一致性,并通过定义新的状态变量与误差,将编队问题转化为一致性问题而解决.