四阶弱对称非负张量Z-谱半径的上下界及应用

雷学红, 许云霞

(凯里学院 理学院, 贵州 凯里 556011)

(1)

另外，等式

(2)

可以用来估计贪婪秩一更新算法的收敛速度[3-4]. 显然，若获得的ρ(A)的上界小于等于‖A‖F，则可以给出式(1)和式(2)的下界.

(3)

Xiong等[6]指出，可以用张量的Z-谱半径表示GMEΨ,即定义纯态|Ψ〉的关联张量为

AΨ=(ai1i2…im)∈Cd1×…×dm

其中ai1i2…im为纯态|Ψ〉的振幅，则式(3)等价

(4)

因此计算GMEΨ的核心问题是估计ρ(AΨ). 因此张量的Z-谱半径的上下界估计是一个值得研究的问题.

1 预备知识

设n为正整数，n≥2，N={1,2,…,n}，R为实数域，Rn为n维实向量组成的集合，R[m,n]为m阶n维实张量组成的集合.设

满足∇f(x)=mAxm-1，则称A是弱对称张量[8].由文献[8]知，对称张量是弱对称张量，反之，不一定成立.

若存在实数λ∈R和非零向量x∈Rn{0}满足:

Axm-1=λx,xTx=1

(5)

则称λ为A的Z-特征值，x为相应于λ的Z-特征向量.用σ(A)表示A的所有Z-特征值组成的集合.称ρ(A)=max{|λ|:λ∈σ(A)}为A的Z-谱半径[8].

非负张量Z-谱半径的界估计引起了广泛关注[9-14]，其中Song等[12]给出了如下估计式:

定理1设A∈R[m,n]是非负张量，则

Wang等[13]给出了四阶弱对称非负张量的Z-谱半径的如下上界：

定理2设A=(ai1i2…im)∈R[m,n]是弱对称非负张量，则

其中

Zhao[14]给出了四阶弱对称非负张量的新上界：

定理3设A=(ai1i2i3i4)∈R[4,n]是弱对称非负张量，且aiiii=aiijj+aijij+aijji,i,j∈N,i≠j，则

本文研究四阶弱对称非负张量Z-谱半径的估计问题，给出了Z-谱半径的一个新上界，改进了文献[12-14]中的结果.

2 主要结果

定理4设A=(ai1i2i3i4)∈R[4,n]是弱对称非负张量，且aiiii=aiijj+aijij+aijji,i,j∈N,i≠j,则

其中

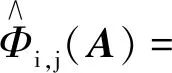
且

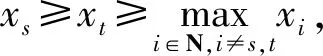
即

(6)

由式(6)得

(7)

由式(7)和xs>0得

(8)

若式(6)中xt>0，由式(5)的第t个分量得

即

(9)

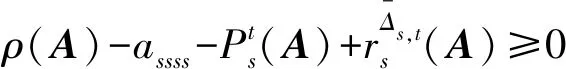
(10)

解式(10)得

(11)

由式(8)和式(11)得

(12)

(13)

由式(12、13)知：

(14)

下面考虑ρ(A)的下界.由式(10)可解得

由ρ(A)≥0可得

(15)

由式(14、15)知，Ω(A)≤ρ(A)≤Φ(A).因此结论成立.

(证毕)

应用与文献[11]中定理11类似的证明，可得

定理5设A=(ai1i2i3i4)∈R[4,n]是弱对称非负张量，且aiiii=aiijj+aijij+aijji,i,j∈N,i≠j，则

由式(4)，并应用类似于文献[6]中定理8的证明，可得如下定理：

定理6给定一个具有非负振幅|Ψ〉∈H的对称纯态，则对于纠缠态|Ψ〉，其纠缠的几何量度GMEΨ满足:

3 数值算例

例1设A=(aijkl)∈R[4,2]是弱对称非负张量，其元素为

计算得(ρ(A),x)=(15.346 0,(0.857 6,0.514 3)T),‖A‖F=20.811 3.

由定理1～定理4和文献[15-22]中相关定理得到的ρ(A)的上界见表1所列.

表1 ρ(A)的上界

由表1可见，由定理4得到的ρ(A)的上界比由定理1～定理3和文献[15-22]中相关定理得到的上界要好，且仅有由定理4得到的ρ(A)的上界Φ(A)小于或等于‖A‖F.此时

且

这表明本例采用贪婪秩一更新算法的收敛速度至少为0.513 9.

例2考虑下面具有非负振幅的4量子2粒子对称态

|Ψ〉=0.6(|0000〉+|1111〉)+0.1(|0100〉+

|0010〉+|0001〉+|1000〉)+0.2(|0011〉+

|0110〉+|0101〉+|1100〉+|1010〉+

|1001〉)

|Ψ〉对应的张量AΨ为

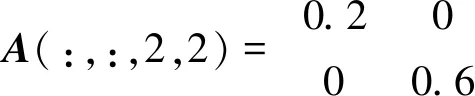
计算得‖AΨ‖F=1,ρ(AΨ)=0.729 9，GMEΨ=0.735 0.由文献[6]中定理7得

1.2≤ρ(AΨ)≤1.5

由式(4)可以看出，由于文献[9]中定理7得到ρ(AΨ)的界大于1，因此该界不能用来估计|Ψ〉纠缠的几何度量. 由定理4得

0.426 8≤ρ(AΨ)≤0.773 2

由定理6得

0.673 5≤GMEΨ≤1.070 7

这表明本例对称纯态|Ψ〉纠缠的几何度量介于0.673 5和1.070 7之间.