自适应有限元法对合金定向倾斜枝晶生长的相场法模拟

朱昶胜, 高宏伟, 马芳兰, 冯 力, 雷 鹏

(1. 兰州理工大学 计算机与通信学院, 甘肃 兰州 730050; 2. 兰州理工大学 省部共建有色金属先进加工与再利用国家重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 网络与信息中心, 甘肃 兰州 730050)

近年来，对于凝固过程的界面形貌演化，不管是在实验、理论还是数值模拟，人们已经做了大量的研究并获得了重要的研究成果[1].一直以来，在传统的研究方法中，合金的定向凝固是研究非平衡体系中由于枝晶形态不稳定而引起竞争效应的标准范式[2].在现代先进的材料制备工艺中，定向凝固技术已被广泛应用，其组织的演化规律对于实际生产具有重要的指导作用.与自由枝晶生长不同的是，定向凝固过程中晶体生长的方向性一方面取决于传热方向，另一方面取决于晶体学上的择优生长方向.例如在均匀过冷熔体中生长的晶体，由于向四周散热速度是一样的，因此其生长方向完全是由晶体界面能的各向异性来决定，晶体沿着界面能最低的方向能够快速生长，最终形成等轴形状的晶体.当热流方向与晶体择优方向不平行时，枝晶的整体结构将会改变其竖直生长的特性，固液界面将会演化成非对称的倾斜枝晶结构[3].Pettersen等[4]首先研究了定向凝固过程中冷却速率对其枝晶生长的影响，其主要目的是研究合金生长的优选方向.Xing等[5]研究了树枝状结构的不对称形态以及错向角对主晶距选择机制的影响,将实验结果与Ghmadh等[6]的相场模拟结果进行对比，表明三维模拟有助于获得更准确的定量结果.Tourret和Karma[7]通过针对错向角进行大量的二维相场模拟，得出通过主晶距的变化，从而导致热梯度对枝晶的生长方向产生影响，且表面张力的各向异性强度也会影响合金阵列生长方向的选择和枝晶形态的变化.

研究了退化海藻向倾斜枝晶转变的机理及其生长动力学，特别研究了温度梯度、抽拉速度和各向异性对凝固方式选择的影响.通过将叶尖分裂不稳定性与侧枝之间发生的关系，讨论了退化海藻倾斜枝晶转变的机理以及其生长动力学.Chen等[9]将射线摄影的实时观察结果与数值模拟结果进行比较，为Al-Cu合金凝固过程中树状枝晶或细胞结构向海藻结构的转变提供了直接证据.其数值结果表明，当噪声足够大时，即使立方原铝固体的晶体首选生长方向与热梯度方向一致，枝晶到海藻的转变也会发生.虽然上述的研究中海藻的结构是处于瞬态的，并且最终实现了稳态树状枝晶生长的微观结构，但足够证明在实际的特殊情况下可以获得对海藻结构有利的条件.Zhu等[10]重点研究了生长方向规定在竖直方向的枝晶生长动力学和定向凝固过程中的形态转变，特别是分析了扰动和各向异性强度对凝固组织的影响，以及定向凝固过程中界面形态的生长机理和海藻组织的转化机理.

由于对所建立相场模型的研究越来越复杂，在计算区域、计算量以及计算精度上的要求也逐渐增加，导致CPU和计算机内存空间的严重负荷，限制了模拟计算的精度，所以采用了自适应有限元方法进行模拟，根据有限元分析结果和事后误差估计来自动地实现网格的加密或粗化，进行网格的自适应调整，以实现用尽可能少的网格数目获得较高精度的解，从而进一步提高了计算效率和求解精度[19].本文采用自适应有限元的方法对Al-Cu(w(Cu)=4%)合金定向凝固过程中倾斜枝晶生长形貌进行深入研究，通过控制固液界面的温度梯度、枝晶尖端的冷却速率、主晶间距以及抽拉速度等参数的变化，得到不同的结晶形态.

1 数学模型

1.1 相场方程和溶质扩散方程

对于Al-Cu(w(Cu)=4%)合金倾斜生长的定量模拟，由于界面宽度选择的影响，相场法模型模拟的尺度都过小，实现起来会有诸多困难，所以将采用薄界面理论分析[11]，使界面宽度的选择大于实际界面的宽度.但是当界面宽度增加后，会产生溶质陷落，这种情况会带来一定程度上的计算误差，为了减小误差，将在溶质场方程中引入Karma等提出的反溶质陷落流[20].以下为所使用的相场模型，其中ψ为1时为固相，ψ为-1时为液相.相场方程为

(1)

通过求解溶质守恒方程的方式得到溶质过饱度U,溶质场方程为

(2)

内部的实际成分C为

C/C0=[1+1-k)U][(1+k)-(1-k)ψ]/2

(3)

方程(2)中的反溶质陷落流jat为

(4)

关于ψ的表达式q为

q(ψ)=(1-ψ)+k(1+ψ)Ds/Dl

(5)

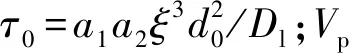
1.2 数值模拟

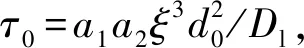
表1 定向凝固过程模拟使用的计算参数

1.3 自适应有限元法

自适应有限元法是一种以误差估计与自适应网格改进技术为核心，通过后验误差估计进行自动调整算法以改进求解过程的数值方法，具有高效率和高可靠性的特点.在自适应有限元方法中，采用各单元基函数的线性组合来逼近单元的实际解.这种方法的优点是它可以将复杂的几何图形离散成单元的网格形状，可以有多种类型，如三角形、矩形和四边形.本文所研究的倾斜枝晶形貌较为复杂，将采用H型自适应有限元法完成网格的加密与粗化的自适应调整.H型自适应有限元法首先在一个较为粗糙的网格上进行求解，根据计算得到的数值结果判断解是否具有要求的精度，然后结合事后的误差估计结果对误差较大的区域进行局部网格加密和粗化，接着计算机重新求解，直至满足精度要求.自适应有限元算法求解相场模型的大致步骤如下：

1) 创建相场模型，在当前网格上对偏微分方程进行求解；

2) 设置相场和溶质场的初始值以及边界条件；

3) 计算后验误差估计，根据后验误差估计对网格进行自适应调整；

4) 若计算结果不满足要求精度，则重复以上步骤.

为了建立高效的自适应网格算法，使用几何等级遗传树法来统一管理网格，完成网格的加密与粗化，具体细化模型如图1，主要有以下操作.如图1a将计算域中每个网格Γ0细化，得到一个均匀的三角形网格，连续细化n次后得到网格{Γn}，最后得到一个以Γ0为根节点的网格四叉树.将每个网格单元记作τ，每个网格单元的指示子记作Eτ，如图1b具体自适应算法为[12]：

1) 局部加密.一个三角形单元τ,如果Eτ>2N+αΞ，其中N和α为控制常数，Ξ为加密粗化偏差，那么该网格τ将被细化，其所有子网格的指示子将被设置为Eτ/2N+α；

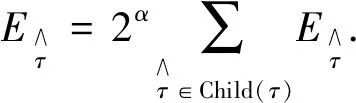
4) 粗化.在几何等级树中由底部向上遍历，对于任意结点，如果它的指示子满足Eτ<2N+αΞ，那么它的所有子孙都将被删除.如图1c所示，由于计算结果的精度要求，需要在求解过程中对初始网格半正则化处理，这样在加密的过程中会出现悬挂点A，B.接着对调整后的网格进行正则化处理，使得整个网格中的单元的每条边都没有悬挂点, M1和M2为双生三角形.在经过正则化处理的网格上建立有限元空间，最终会实现偏微分方程的高效求解.具体的半正则化和正则化算法参考文献[12].

图1 几何等级遗传树管理网格的细化模型Fig.1 Refinement model of geometric hierarchical genetic tree management grid

采用自适应有限元方法求解相场方程,这种方式既可以根据方程需求对区域进行合理形状的网格划分，又可以根据指定场的函数需求将节点进行排列，所以对区域形状有良好的适应性.

2 结果和讨论

2.1 相场模型的自适应有限元法求解分析

数值模拟方法的不同会对方程的处理、计算模型结果以及计算效率有很大影响.采用基于自适应有限元法求解相场模型，如图2a为初始网格，图2b为生长时间t=0.3 s时的枝晶生长形貌，图2c为框处放大后的结果.可以发现，在固液界面区域A处网格密度相对稠密，而远离界面的B、C、D区域网格相对稀疏.通过这种稀疏分布的网格方式，导致自适应有限元网格节点相对较少.随着求解时间的推移，节点的数量随即增加，在t=0.3 s时，节点数为2.79×105，远小于采用均匀网格法计算时1.6×106的节点数量[9]，二者相比少了一个数量级，所以采用自适应有限元法大大降低了计算量，有效提高了计算效率.此外，采用非零元素存储法存储系数矩阵时，自适应有限元法对应系数矩阵所占用的存储空间为M1～L，而均匀网格占用的存储空间M1～L2，相比较，自适应有限元法所需要的存储空间低了一个数量级，这对于较大规模的数值模拟计算效率会有提高.将自适应有限元法的CPU使用时间Ta和均匀网格法的CPU使用时间Tu进行对比，如图3所示，在相同计算域LB大小的情况下，自适应有限元法的CPU使用时间远小于均匀网格法，可知自适应有限元法的计算效率要远高于均匀网格法.图4为两种数值模拟所得加速比，可以看出，随着计算域的增大，自适应有限元法的计算效率越高.

图2 采用自适应有限元法网格图

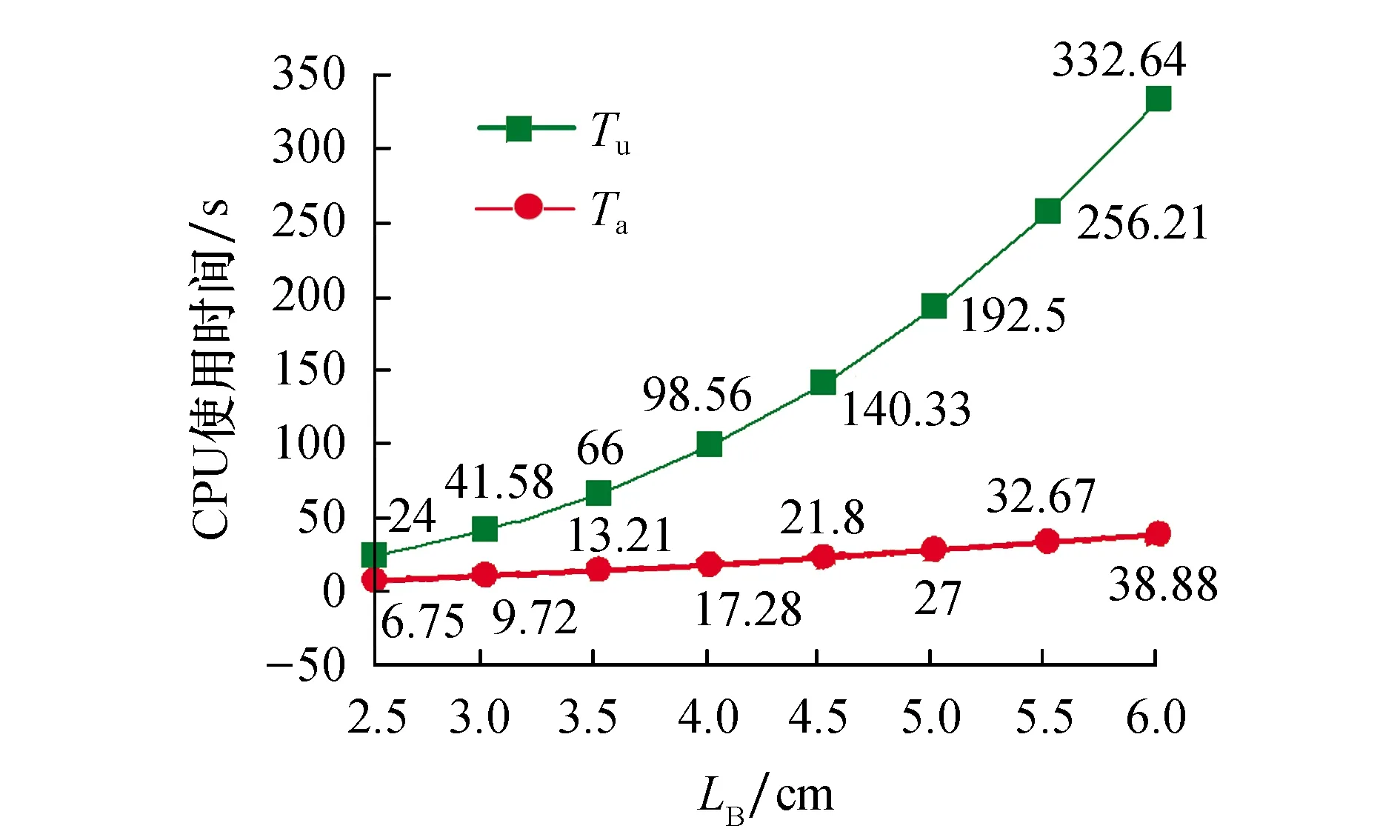
图3 采用自适应有限元法和均匀网格法CPU使用时间

图4 均匀网格法和自适应有限元法的加速比

自适应有限元法的CPU使用时间Ta，均匀网格法的CPU使用时间Tu以及加速比Tu/Ta公式为

(6)

2.2 冷却速率对界面形貌的影响

在定向凝固的研究过程中，首先模拟了热流方向与晶体择优方向平行时，固液界面按竖直方向生长的海藻状枝晶，如图5所示，上半部分为模拟定向凝固的相场图，下半部分为溶质场图，这是枝晶定向凝固中最为普遍的例子.当热流方向与晶体择优方向不平行时，设定枝晶优选生长的错向角φ0=π/6，冷却速率分别设定为R=0.032 K/s，R=0.12 K/s，R=0.24 K/s，其他参数均见表1，图6a～6c分别为3种不同冷却速率下树枝状枝晶的瞬态演化，可以看出，在不同的冷却速率下，枝晶的形貌有很大不同.

图5 热流方向与晶体择优方向平行时固液界面变为按竖直方向生长的海藻状枝晶

图6 Al-Cu(w(Cu)=4%)合金在3种不同冷却速率下的树状枝晶形态Fig.6 Dendritic morphology of Al-Cu(w(Cu)=4%) alloys at three different cooling rates

当R=0.032 K/s时，枝晶的生长方向更加倾向于晶体的优选生长方向π/6，且出现了第三枝晶臂.当冷却速率R=0.12 K/s时，枝晶的实际生长方向偏离了晶体的优选生长方向，向温度梯度方向靠拢，偏向角度为π/9.当冷却速率达到R=0.24 K/s，枝晶的实际生长的角度更加靠近温度梯度的方向，基本与温度梯度角度相吻合，偏向角度为π/36，枝晶形貌呈现出较为规则的树枝形貌.总体而言，枝晶的原始生长角度与冷却速率有很大的关系.界面过冷度是控制枝晶生长的一个关键因素，随着冷却速率不断增大，界面过冷度也随之增大，从而控制了枝晶生长角度的偏差，枝晶的生长角度从晶体的优选生长方向π/6逐渐向π/36偏移.

枝晶由细胞状向树状演变的过程中，图7a～7c为从胞状向树状枝晶过渡和尖端分裂的进化序列，观察图7所表示的枝晶的初始状态，当冷却速率R=0.032 K/s时，此时界面过冷度很小，图7a中黑色虚线标注上方，枝晶尖端处出现了明显的分裂现象.当冷却速率达到R=0.12 K/s时，从图7b可以看出，枝晶尖端的分裂现象减少，只有个别尖端出现分裂.随着冷却速率的不断增加，界面过冷度也随之增大，枝晶中靠向温度梯度方向的尖端受到青睐.如图7c冷却速率达到R=0.24 K/s时，枝晶的尖端没有了明显的分裂现象.Amoorezaei等[18]曾报道了界面过冷度和溶质之间的相互作用将会大幅度的影响尖端分裂，以上现象与他的理论是一致的.

图7 定向凝固组织形态在冷却速度分别为R=0.032 K/s，R=0.12 K/s，R=0.24 K/s的变化Fig.7 The changes of the directional solidification structure at the cooling rate of R=0.032 K/s, R=0.12 K/s, R=0.24 K/s

通过观察图7d溶质场中枝晶的生长形貌，可以看出，枝晶内部的溶质浓度要明显低于枝晶间隙的溶质浓度，这是由于溶质偏析的影响(合金中各组成元素在结晶时分布不均匀导致).当冷却速率较低时，固液界面的移动速率非常缓慢，溶质的扩散在凝固的过程中发挥着主要的作用，因此枝晶出现了不稳定性，并且沿着高对称的晶轴发生触发，所以枝晶的生长不易发生改变，更倾向于晶体的原始方向.但是随着冷却速率的不断增大，界面的过冷度也随即快速增大，此时热释放主导了界面演化，从而影响枝晶生长方向和界面速度的变化，枝晶的角度由原始的择优晶体方向逐渐向温度梯度方向转变.

如图6a～6c所示，冷却速率从R=0.032 K/s转变到R=0.24 K/s的同时，枝晶的生长方向也由原始的择优晶体方向φ0=π/6转变到φ0=π/36.由此可见，冷却速率很小时，具有控制枝晶生长有关键作用的过冷度也很小，此时溶质的扩散是完全的，所以热流方向的枝晶沿着择优取向不断生长.随着冷却速率的增加，尖端过冷度随即不断增大，热萃取控制了取向角的偏差，使枝晶的生长角度向温度梯度方向发生偏转.

2.3 间距(Péclect数)对界面形貌的影响

对倾斜枝晶实际生长方向与热流方向的夹角α和晶体择优取角φ0之间的变化规律进行模拟.由图8可以看出，在Al-Cu(w(Cu)=4%)合金的定向凝固过程中，当晶体的择优生长方向与温度梯度方向不一致时，枝晶的实际生长方向位于晶体的择优方向与温度梯度方向之间.当晶体的择优生长方向分别为φ0=10°，20°，30°时，枝晶的实际生长方向为α=7.85°，13.92°，22.08°.这与枝晶的间距λ和枝晶的生长速度V有很大的关系，并且随着将晶体择优取角的数值调整大，枝晶尖端的分裂更加剧烈.以上现象与Deschamps和Pocheau等[13-14]实验给出的结果相吻合.

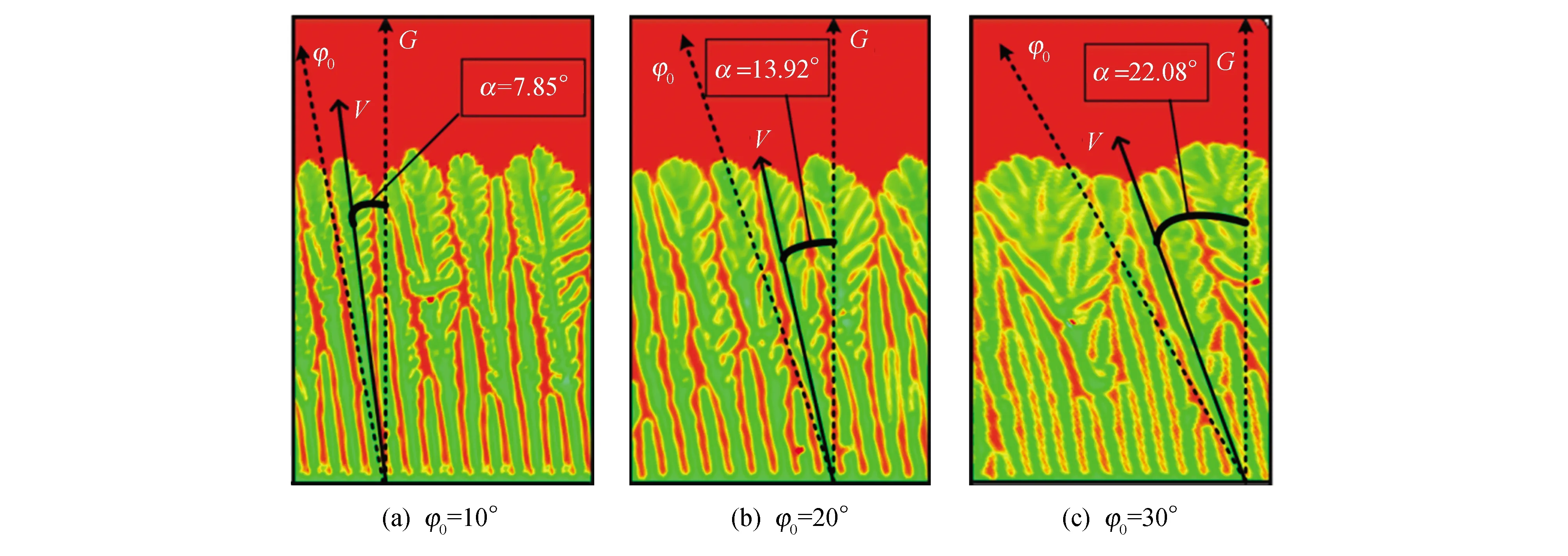
图8 V=110 μm，λ=140 μm时枝晶的实际生长方向α随晶体择优方向φ0的变化 Fig.8 When V=110 μm and λ=140 μm, the actual growth direction α of the dendrite varies with the crystal preferred direction φ0

枝晶之间的间距Péclect数，在理论上定义为Pe=λV/Dl.设定三个晶体择优方向，φ0分别为10°、20°和30°，并计算枝晶实际生长角度α与晶体择优取向角φ0之间的比值，通过记录三个角度随着Pe变化的α/φ0值，观察其变化的情况.Pocheau等[15]通过大批实验数据得出关于主晶间距Pe、晶体择优取向角φ0和枝晶实际生长角α之间的经典公式：

(7)

其中：a和b均为拟合参数，通过以上经典公式并拟合10°、20°和30°三个择优角度的计算数值绘制曲线，计算得出当φ0=10°时拟合参数为a=0.63,b=1.32；φ0=20°时拟合参数为a=0.49,b=1.66；φ0=30°时拟合参数为a=0.31，b=1.98，可知模拟结果基本吻合公式(7).通过图9可以看出，随着Pe的逐渐增大，10°、20°和30°对应的α/φ0值也逐渐增大，慢慢趋近于1.以上模拟结果表明，随着枝晶间距Pe值的逐渐增大，α值逐渐趋近于φ0值，即随着主晶间距和抽拉速度的增大，枝晶的实际生长角度也逐渐从温度梯度方向向晶体择优方向偏转，这与Pocheau等[14-15]给出的实验结论一致.

图9 φ0分别为30°，20°，10°时α/φ0随Péclect数变化规律Fig.9 When φ0 is 30°, 20°, 10°, α/φ0varies with Pe number

3 结论

使用了自适应有限元法求解相场模型，解决了传统方法解决相场模型计算量大、计算效率低等缺点.研究了Al-Cu(w(Cu)=4%)合金的定向倾斜枝晶在温度梯度固定的情况下，冷却速率、主晶间距对形貌演变的影响，结论如下：

1) 随着冷却速率的增大，热萃取控制了取向角的偏差，枝晶错向角向温度梯度方向偏转.不同的冷却速率会影响树状枝晶尖端分裂的不稳定性，导致枝晶形貌较为复杂，向海藻状过渡.

2) 倾斜枝晶的实际生长方向位于温度梯度与晶体择优取向角之间，并且随着一次主晶间距Pe值和抽拉速度的逐渐增大，枝晶的实际生长角度也逐渐从温度梯度方向向晶体择优方向偏转.

3) 自适应有限元法相较于均匀网格法在网格节点数、网格占用的存储空间和CPU的运行时间上均低了一个数量级，并且随着计算域的增大，自适应有限元法的计算效率越高.