浅谈高中数学课堂上启发性教学方法的应用
——以“直线与圆的位置关系”(人教版必修2)为例
☉安徽省六安第二中学 易 欢
一、引言
高中数学教学相对于初中数学教学而言,无论是教学内容还是教学广度和教学深度都明显增加.知识点多而分散是高中数学教材的一大特点,因此高中学生学习高中数学知识有一定难度,教师的教学之路任重道远.虽然教师授课时间有限,但是可以带领学生找到数学学习的规律,理解记忆,整理分类,总结归纳.这样不仅可以提高学生的逻辑思维能力,而且可以让学生将各个学习过程中所学知识串联起来,形成完整的知识体系.本文以人教版高一数学必修2教材中第四章第二节直线与圆的位置关系为例,浅谈高中数学教学启发.
二、高中数学直线与圆的位置关系
通过计算直线与圆的交点,我们可以将直线与圆的位置关系总结为:如果一条直线与一个圆有两个交点,那么我们认为这条直线与这个圆相交;如果一条直线与一个圆有且只有一个交点,那么我们认为这条直线与这个圆相切;如果一条直线与一个圆没有任何交点,那么我们认为这条直线与这个圆相离.需要补充的是:在直线与圆相交时,通常将这条直线叫做这个圆的割线;在直线与圆相切时,通常称这条直线为这个圆的切线,直线与圆的公共点叫切点.
三、高中数学直线与圆的位置关系的启发性教学方法
(一)明确目标,理清重难点
教师在进行每个章节的数学知识教学时,要明确教学目标,为学生理清重点和难点.就直线与圆的位置关系这一小节而言,教学目标是让学生能够概括其定义,并且会使用定义来判断和应用直线与圆的位置关系;教学重点是帮助学生理解并掌握直线与圆的相切、相离、相交三种位置关系;教学难点是引导学生运用并掌握直线与圆的判定方法.在明确教学目标和理清重难点之后,有助于教师通过讲解具体的案例,培养学生认知和理解直线与圆的三种位置关系的能力;有助于教师通过将点与圆的位置关系和直线与圆的位置关系进行对比讲解,加深学生对直线与圆的位置和数量关系的理解.
(二)讲练结合,应用新知识
数学教学的展开离不开例题讲解,学生结合课堂练习与教师讲解,能够及时运用和消化新知识,巩固已经学过的知识.这个阶段需要发挥教师的主导作用,充分发挥课堂教学的激励和调控功能.但是,教师在进行讲练结合的时候也应该注意,应该层层递进,慢慢加深学生对新知识的理解.
案例1 如图1,Rt△ABC中的斜边BC=10cm,直角边AC=6cm.那么试判断:以A为圆心,半径分别为2cm、4cm的两个圆与直线BC有怎样的位置关系?以A为圆心的圆半径r多长时,才能判定直线BC与⊙A相切?以A为圆心的圆半径r多长时,才能判定直线BC与⊙A相交?
解析:在Rt△ABC中,由勾股定理得AB=8cm,所以BC边上的高为4.8cm.
因为4.8cm>4cm>2cm,故以A为圆心,半径分别为2cm、4cm的两个圆与直线BC相离;以A为圆心的圆半径r为4.8cm时,才能判定直线BC与⊙A相切;以A为圆心的圆半径r大于4.8cm时,才能判定直线BC与⊙A相切.
评析:该例题看起来简单容易,只需将直角三角形斜边上的高计算出来,问题就迎刃而解.但是,无论任何学科,基础知识是关键.实际上,这个题目将圆与直线的位置关系的定义与判定都囊括其中.然而,越是简单基础的问题,学生在练习时就越容易出错.所以,教师在进行例题讲解时需要重视这类基础例题,学生在进行课堂练习或完成课下习题的过程中也不能松懈基础训练.因此,教师在课上讲解这类简单例题时,一方面,很容易被学生接受,快速结合课堂知识进行练习并告诉老师答案;另一方面,能够将教学目标与重难点结合起来,通过学生的课堂练习反馈进行进一步教学.
案例2 在平面直角坐标系中,已知圆的方程为圆心为P,现有过点Q(0,2)且斜率为k的直线,若与圆P相交于A、B两点,求斜率k的取值范围;若与圆P没有交点时
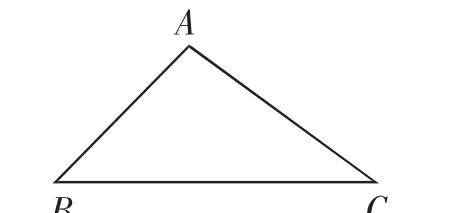
图1
,k的取值范围又为多少?
解析:根据已知条件可以得到圆P的圆心坐标为(6,0),半径是2.
设过点Q的直线为y=kx+2.
想要满足题目中直线与圆相交于两点,则需要圆心到直线之间的距离小于半径,根据所学点到直线的距离为d,d<2.即可解出k的取值范围为
若与圆P没有交点,则圆心到直线的距离需要大于半径
评析:案例2比案例1的难度有了提高,做到了层层深入.将圆与直线的位置关系放在了直角坐标系中,若此题采用代数方法,将直线方程代入圆的方程,根据解的个数,采取判定式作答,则此题计算量较大.但是学生若可以做到将代数与几何知识巧妙地融合,则大大减少了计算量,提高了解题效率.通过这种综合性的训练,可以提高学生的综合解题能力.将新知识与旧知识进行结合,达到融会贯通的目的.
(三)寻找规律,总结归纳
高中数学虽然知识点罗列散乱,但是仍然有规律可循.学生要将众多知识点理解并掌握,离不开总结归纳.然而,高中数学知识也不仅仅局限于书本,学生还应该善于发现和总结各个知识点的规律,这就需要教师在教学过程中引导学生养成自主学习、善于思考总结的好习惯.
案例3 如图2,已知直线PB与⊙O相交于点A,割线为直线PAB,并且有以下条件:PA=7cm,AB=5cm,PO=10cm,试求⊙O的半径.
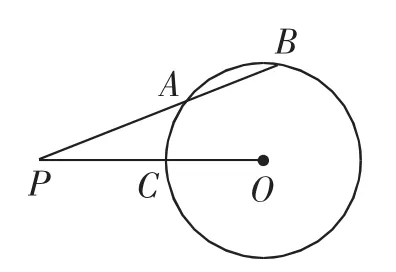
图2
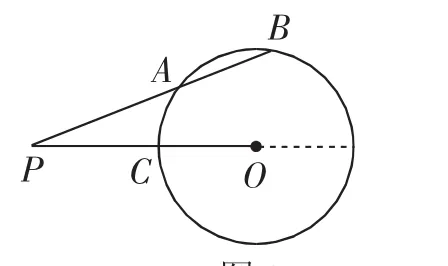
图3
解析:延长PO交⊙O于点D,因为⊙O的割线为直线PAB,由割线定理知PA·PB=PC·PD. 因为PC·PD=(POCO)(PO+OD),所以PA·PB=(PO-CO)(PO+OD),因为PA=7cm,AB=5cm,PO=10cm,OD=CO,将数据代入PA·PB=(PO-CO)(PO+OD)中,解得CO=4cm.所以⊙O的半径为4cm.
评析:这类题型比较复杂,因为人教版高中数学必修2的教材中没有给出割线定理的具体表达式.但同时,这类题型立足于直线与圆的位置关系的基础之上,以直线与圆相交的性质为出发点,又在考查割线的性质和定理.这需要教师在数学课堂教学中发挥学生的主动学习作用,通过例题练习和讲解,引导学生总结出割线定理,加深学生对割线定理的理解与应用,便于学生在以后涉及割线定理的题型中快速完成解答.
案例4 已知直线表达式为Ax+By+C=0,圆的表达式为x2+y2+Dx+Ey+F=0.判定直线与圆的位置关系.
思路一:已知直线表达式为Ax+By+C=0,圆的表达式可以化为(x-a)2+(y-b)2=r2,通过判断圆心(a,b)到直线的距离可以判定直线与圆的位置关系.
圆心(a,b)到直线的距离可以表示为后判断d与圆的半径r的大小关系,即可得到直线与圆的位置关系:如果d=r,则直线与圆相切;如果d<r,则直线与圆相交;如果d>r,则直线与圆相离.
思路二:已知直线表达式为Ax+By+C=0,圆的表达式为x2+y2+Dx+Ey+F=0.将这两个方程联立消元后得到一个方程ax2+by2+cx+dy+e=0.然后根据方程的判别式作答.若判别式大于零,则表示方程有两个解,即圆与直线有两个交点;若判别式等于零,则表示方程有一个解,即圆与直线有一个交点,直线与圆相切;若判别式小于零,则方程无解,圆与直线没有交点.
评析:这个案例考查的就是直线与圆的位置关系的两种判别方法:几何法和代数法.思路一就是几何法,通过比较圆的半径与圆心到直线的距离的大小,判定直线与圆的位置关系;思路二就是代数法,结合直线与圆的数学表达式,消元之后得到一个一元二次方程,通过计算这个一元二次方程的判别式与零的关系判断直线与圆的位置关系.这两种方法在人教版高中数学必修2的教材中都有提到过,但是需要教师引导学生进行总结归纳,使学生不至于在面对不同的题型时混淆方法,便于学生对直线与圆的位置关系的判别方法理解的更加扎实和掌握的更加牢固.
四、总结
面对应试教育和素质教育,高中数学教学任务艰巨,学生学习压力巨大.但是,教无定法,教学有法.教师的使命是教学,教授学生知识和帮助学生学习,因此教学方法显得尤为重要.通过人教版高一数学必修2教材中第四章第二节直线与圆的位置关系的教学,针对高中数学教学,我们可以得到三点启发:第一,“明确目标,理清重难点”的教学方式,有助于学生快速吸收课堂知识,高效学习数学知识的重难点;第二,“讲练结合,应用新知识”的教学策略,有助于学生巩固课堂基础知识,并将新知识学以致用;第三,“寻找规律,总结归纳”的引导教学,有助于学生对高中数学知识点理解的更加透彻,掌握的更加牢固.F

