高中数学“对话”式教学案例分析
☉浙江省温岭中学 陈素凤
一、教学对话
以沟通和交流为基本形式特征所进行的动态行为就是我们经常研究的“教学对话”,教师在对话式教学中应首先研究具体的教学内容,并选择恰当的教学方法为学生的积极探究营造出良好的教学情境,使学生能够在自己的思考中获取知识与思维能力的发展.新课程一直倡导的学生主体也能在“教学对话”中得到有力的凸显,思想与思想碰撞的师生对话对新型师生关系的培育也能起到非常积极的作用.
二、教学对话的现状
对话式教学方法的提倡导致当前课堂教学出现了高密度对话的现象,课堂教学因为“满堂问”的教学变得热闹异常,但学生在这样的高密度对话中却收益甚少.事实、记忆类的一般常识型问题往往使师生之间的对话丧失了应有的“悬念”,“假对话”、“空对话”、“伪对话”往往无法启发学生思考知识的综合应用,学其形却不见其神的教学对话表面热闹却不能有很多实质上的效益.怎样才能在课堂教学中落实真正有效的双边对话也因此成为了广大教师思考的问题.
(一)把握时机促进有效互动
1.建立在学生体验上的对话
“狂轰滥炸”式的提问是当前好多教师在对话教学中不经意间就容易表现出的教学行为,很多教师在学生还未对问题形成思考与体验时就开始分析讲解了,有的教师在问题提出后的很短时间内不等被提问学生作出回答就提出其他问题或请其他学生作答,学生在这样的状态下根本无法对问题形成自己的思考,更加谈不上表现自己的观点了.
学生在知识的领会上当然比不得具备一定经验与知识的教师,因此,教师在提问后应给学生充裕的思考空间并在学生形成体验之后请学生作答,此时的学生才会更加乐意作答并积极表达出自己的观点.
2.建立在学生感悟上的对话
有些教师喜欢把话到嘴边的答案留给学生作答,学生在教师一连串的分析提示中根本无法形成自己的思维,在教师明确指点的“光明大道”上也就无法进行自己的选择,有的教师还将自己的这一行为理解成这是自己对学生的引导,认为自己很好地帮助了学生进行解题.
但这些教师将数学课堂教学应引导学生亲身经历知识的形成并进行再创造的这一重要使命完全忘记了,学生在教师干预过多的教学中根本无法对数学事实建立自己应有的情感体验与理性认识.因此,教师在对话式教学中一定要给学生预留探索空间,使学生能够在自身已有知识、经验的基础上形成自己的感悟,并促成自身认知的变化与加深.
3.建立在学生生成上的对话
很多教师为了让学生在思考问题时少走弯路,因此在学生还没思考出答案之前就会给出解题的正确思路,这种为学生搭建整体框架的教学方式虽然能让学生在细节上进行思考,但学生却失去了自主构建知识框架的机会.教师不能放手让学生自主构建知识框架大多都是考虑自身教学计划与任务导致的,事实上,教师如果能够在学生需要的地方适时科学地帮助学生构建知识框架,学生必然能够更好地体会知识并建立深刻的感悟,教师再根据学生在课上的生成灵活调整自己的教学,也能更好地展现教师的教学水平.
(二)如何落实教学对话
1.有效设问促使学生参与对话
教师根据学生的知识水平与经验将教学内容进行整合与分层能够将抽象的教学目标设计成不同层次并相互联系的问题,这些知识的分层推进能使学生深刻感悟知识形成过程中的逻辑,这些能够发展学生个性思维的问题为学生搭建了合理的对话框架,师生之间的对话在有的放矢的问题引领中探触到了知识的本质.
案例1 直线的倾斜角.
师:请大家在稿纸上将经过一点的数条直线作出来,并观察一下它们之间的区别.
生:形成了好多不同的角.
师:假如我们将角的顶点视作直线和x轴的交点,你认为角的两条边是什么呢?
生:x轴和角的终边.
师:大家知道角的形成有哪几种方式吗?
生:顶点两射线或者一射线绕一点旋转而形成.
师:直线在直角坐标系中与x轴形成的角我们称之为倾斜角,大家想一想是不是每一条直线都会有倾斜角呢?
生:是.
师:同学们有没有想过直线与x轴重合或平行时的倾斜角应该是多大?
生:0°.
师:说成180°可以吗?
生:不可以.
师:那大家是否能够概括倾斜角的倾斜程度呢?
生:0°(可取)——180°(不可取).
师:能够刻画直线倾斜程度的概念又是什么呢?
生:斜率.
师:大家想一想是不是每一条直线都有斜率呢?
生:……
师:倾斜角不是90°时就都有斜率,大家想一想使用倾斜角与斜率又有哪里不同呢?
生:两者分别是从几何的角度与代数的角度来刻画直线的倾斜程度的.
师:倾斜角为钝角时的斜率怎样?
生:斜率小于0.
师:如果直线的斜率不是负值时,那么倾斜角又是怎样的呢?
生:小于等于90°.
师:大家从今天的讨论中可有什么体会?
2.引导学生在情境探究中进行深层对话
教师在精心设计的情境中引导学生类比、引申、发散,能使学生在深度探究中交流困惑并产生有意义的思维碰撞,并在深层对话中形成对知识的领悟与建构.
探索活动1:
(1)一个复数成为实数必须具备哪些充要条件?
(2)复数成为实数的充要条件为应怎样证明?
(3)你能从问题2上又提出一些什么问题呢?
命题汇总:①类比提问:一个复数成为虚数应该满足哪些充要条件?②变式提问:从能推出什么?③发散提问必为实数,是什么?是什么?
探索活动2:
(1)观察函数y=cos x(图1)与y=sin x的图像(图2)并找出函数奇偶性、周期性与图像对称性的相关结论.
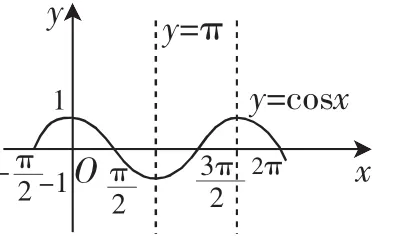
图1
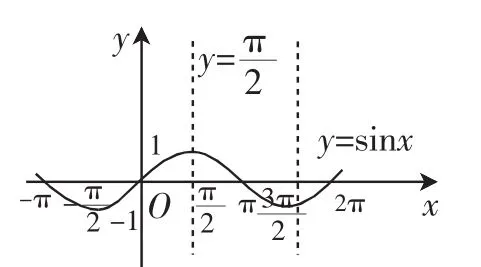
图2
(2)还有类似这样的函数吗?
(3)你还能举出与这两个函数性质相似的函数吗?
(4)请尝试构造一个或几个能同时具备函数“三性”的函数.
(5)你能尝试从函数“三性”之间的相互关系来进行命题吗?
(6)对自己提出的命题进行证明、类比、推广与发散.
成果展示:已知函数y=f(x)是偶函数且关于直线x=1对称,当x∈[0,1]时,f(x)=x2,作函数图像.观察图3可知函数具有周期性,周期是2.
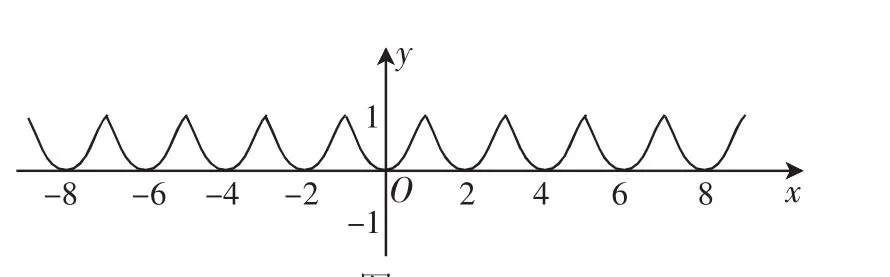
图3
这一函数还可以这样描述:
(1)已知函数y=f(x)是偶函数且f(x+2)=f(x),当x∈[0,1]时,f(x)=x2.
(2)已知函数y=f(x),满足f(x+2)=f(x)且f(1-x)=f(1+x),当x∈[0,1]时,f(x)=x2.
不同的描述得到同一个函数说明了已知函数存在三个论断:
①f(-x)=f(x);②f(2-x)=f(x);③f(2+x)=f(x).
因此,如果将其中两个论断作为条件,则剩余的那个论断就可以作为结论,所以函数y=f(x)可以作出猜想:①f(-x)=f(x);②f(2a-x)=f(x);③f(2a+x)=f(x).
经过探索可知论断②、论断③必须具备相同的2a,推广这一结果可得:
(1)y=f(x)的图像关于直线x=a对称;
(2)y=f(x)的图像关于直线x=b对称;
(3)y=f(x)为周期函数,周期T=2|b-a|是其中一个周期.
经过类比、发散可知:
(1)若函数y=f(x)是偶函数且其图像关于点A(a,0)对称,则函数y=f(x)是周期函数且周期为T=4|a|.
(2)若函数y=f(x)是奇函数且其图像关于直线x=a对称,则函数y=f(x)是周期函数且周期为T=2|a|.
(3)若函数y=f(x)是奇函数且其图像关于点A(a,0)对称,则函数y=f(x)是周期函数且周期为T=2|a|.
总之,师生之间、生生之间的双边互动对话能够有效促进师生双方认知、思维水平的逐步提升,因此,教师应重视对话的设计并对学生在对话中的生成作出积极的回应,使得学生与教师之间产生有意义的交流并因此实现课堂教学活动的活力.F

