不同版本教科书中例习题难度比较研究
——以人教A版和北师大版中“平面向量”为例
☉西北师范大学教育学院 白若雪
一、引言
在高中数学课程中,几何是变化较大的内容之一,也是贯穿高中数学课程中的一条主线.几何课程的设计分为两部分,一部分是将“把握图形”的能力作为指导思想,贯穿在整个数学课程的始终.另一部分是设计了应用的几何内容.
向量是几何的一个基本内容,它既可以看成是代数的内容,也可以看成是几何的内容.向量可以用来表示空间中的点、线、面.如果以坐标系的原点为起点,向量就与空间中的点建立了一一对应关系.通过向量的运算来度量几何体现了向量是连接几何和代数的一座天然“桥梁”,它进一步体现了解析几何的思想,是体会数形结合思想的重要载体.
本文重点是两本数学教材对于平面向量例习题的难度比较,指出各教材的共性和差异,优点和不足,为中学选择教材提供帮助.
二、研究方法
(一)研究对象
人教A版教材中平面向量的知识安排在必修4第二章,分为5小节,北师大版教材平面向量知识也安排在必修4第二章,分为7小节.探究两版本教材中平面向量内容中的例习题的编排特点.
(二)研究方法
选择了鲍建生教授的“数学课程的综合难度模型”,该模型是由5个因素构成的五边形,这5个因素分别是认知、背景、运算、推理、知识含量,其中每个因素又都细化为不同的层次水平.
(三)研究内容
例习题既是向学生传授知识的纽带,又是巩固“双基”、培养能力的桥梁.研究主要针对例习题的呈现形式、题量、难易程度等方面进行相互比较.
三、研究结果分析
(一)例习题的形式与数量比较

表1 人教A版教材向量例习题数量统计表[1]

表2 北师大版教材向量例习题数量统计表[2]
由表1和表2可知北师大版的例习题总数要少于人教A版,其中人教A版涉及的探究与思考类型较多,数量也远多于北师大版,似乎更注重“探究式教学”.
从整体观察两个版本的例习题编写形式,还是有很多相似之处的,比如,都是先安排例子作为引入,然后分析,中间穿插探究或思考,这些都符合教师的教和学生的学的规律,只是人教A版的内容丰富些.
(二)综合难度比较
例习题的综合难度可衡量出教科书编写者对学习者所要达到的要求,本文采用经李淑文博士改进后的鲍建生数学题综合难度多因素模型,如表3.
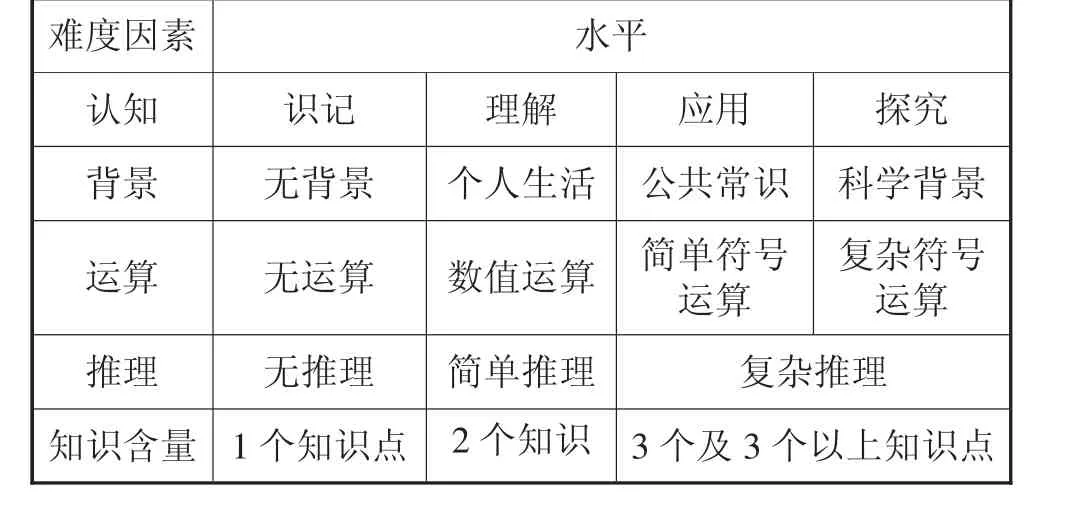
表3 维度分析表
人教A版与北师大版向量例题各难度因素的难度值统计如表4所示.
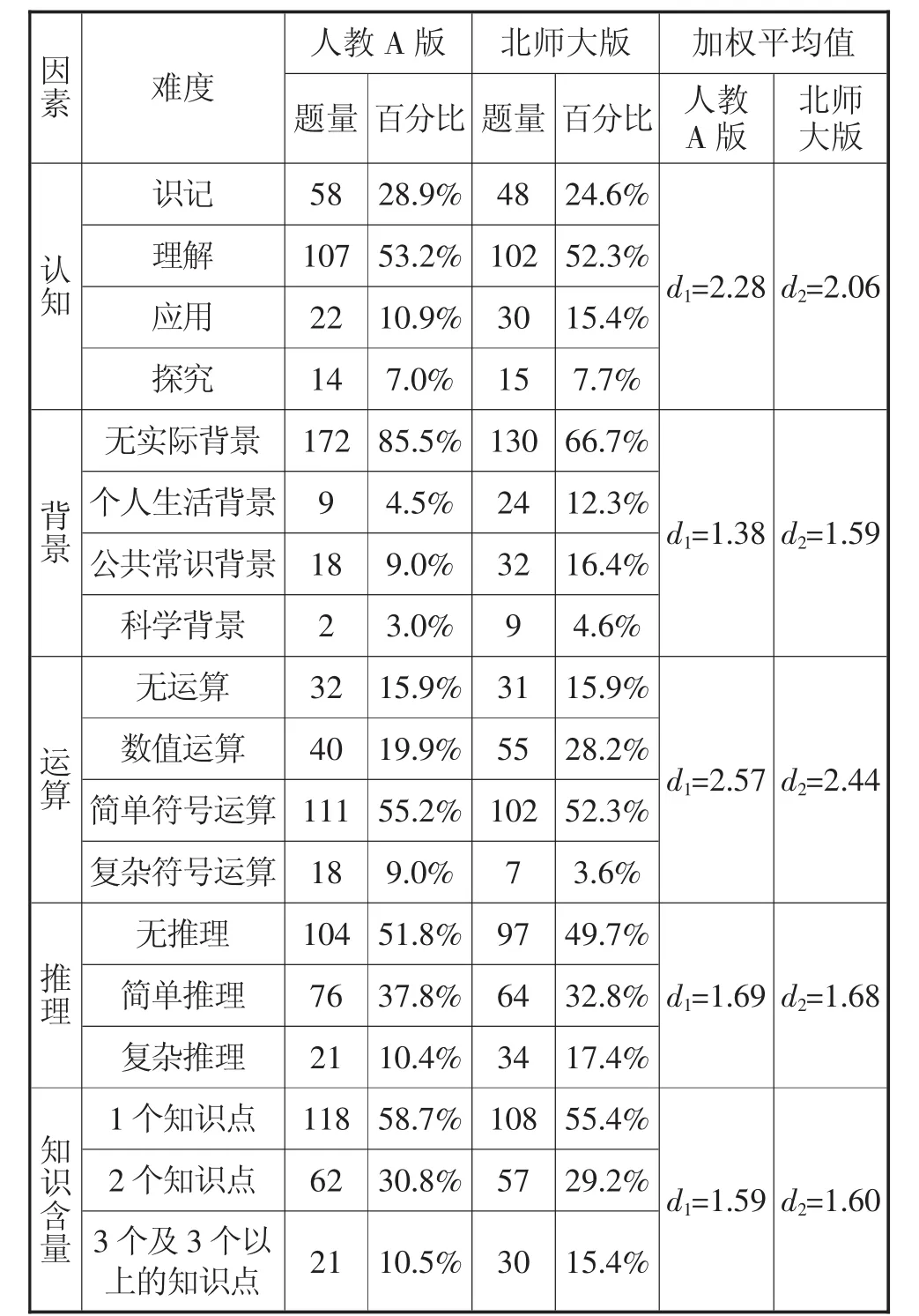
表4 两套教材例习题难度因素对照
说明:加权平均d的计算公式为i=1,2,3,4,5;j=1,2,…).[3]
其中,di依次表示“认知”“背景”“运算”“推理”“知识含量”五个难度因素的加权平均值,dij为第i个难度因素的第j个水平的权重(依水平分别取1,2,3,4,5),nij则表示这组题目中属于i第个难度因素的第j个水平的题目的个数,其总和等于该组题目的总数n.
根据两套教材各难度因素的加权平均值画出两套教材向量例习题综合难度五边形如图1所示:
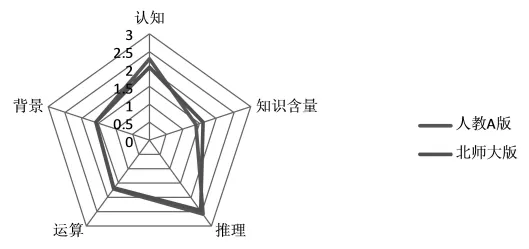
图1 两套教材例题综合难度五边形
这个五边形很直观地显示出:在背景、知识含量2个因素上,人教A版教材数学例习题难度要低于北师大版,而在运算、推理、认知3个因素上,人教A版教材数学例习题难度要高于北师大版,而在这5个因素中,背景的难度值相比其他因素要小很多,两个版本都没有保持5个因素的平衡性.
(1)认知因素的水平比较.
从表4中可以看出人教A版教材的201个例习题在认知的4个水平上的表现是:识记水平的占28.9%,理解水平的占53.2%,应用水平的占10.9%,探究水平的占7.0%.而北师大版教材195个例习题在认知的4个水平上的表现是:识记水平的占24.6%,理解水平的占52.3%,应用水平的占15.4%,探究水平的占7.7%.如图2所示.
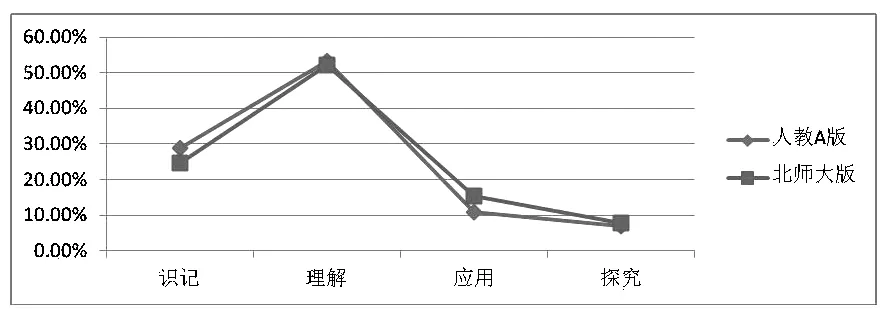
图2 两版本在认知水平上的比较
从图2可以看出,在认知的4个水平上人教A版在识记和理解两个因素的难度值都要高于北师大版,但总体都呈现的是一个变化趋势.两套教材的探究水平体现的都比较低,而重点强调学生的理解水平和应用意识,这也体现了《普通高中数学课程标准》(实验稿)对于数学课程的要求:“高中数学课程有助于学生认识数学的应用价值,增强应用意识,形成解决简单实际问题的能力.”
(2)背景因素的水平比较.
统计表明人教A版在平面向量这一章中的例习题有85.5%的无实际背景,4.5%的是个人生活背景,9.0%的是公共常识背景,3.0%的是有科学背景.在北师大版的例习题中有66.7%的无实际背景,12.3%的有个人生活背景,16.4%的有公共常识背景,而有科学背景的占4.6%.如图3所示.
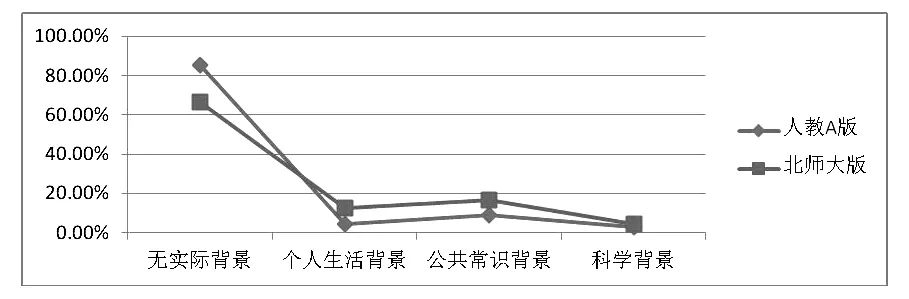
图3 两版本在背景水平上的比较
从图3可以看出两套教材都以无实际背景例题为主,这可能是由于学生的发展过程决定的,在高中阶段学生的学习方式已经由初中阶段的半抽象、半具体转变为可以依靠完全抽象思维来解决数学问题,所以不用通过很多的背景材料来激发学生的兴趣.而北师大版注重公共常识背景题和科学背景题,读过两本教材的读者不难发现北师大版中的数学例题包含实例分析和例子里面很多都会涉及物理方面的知识,我们知道向量最初被应用于物理学,很多物理量如力、速度、位移,以及电场强向量度、磁感应强度等都是向量.体现了向量在解决问题时的有效性,学生所学到的向量知识不是简单的计算及证明,而是能够应用于生活及科学的一个工具.
(3)运算因素的水平比较.
人教A版教材的201个例习题有15.9%的是没有运算的,19.9%是数值运算,55.2%的是简单符号运算,9.0%的是复杂符号运算.北师大版教材的195个例习题有15.9%的是无运算的,28.2%是属于数值运算,52.3%的是简单符号运算,3.6%的是复杂符号运算.如图4所示.
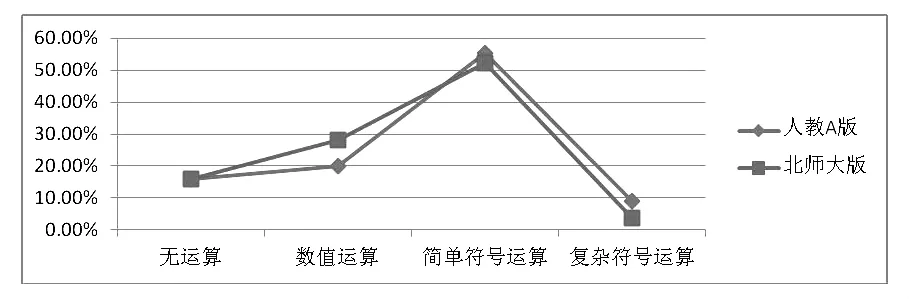
图4 运算因素的水平比较
在运算因素的水平比较图中不难看出人教A版只有在数值运算的例习题中略低于北师大版,而在其他的3个水平无运算、简单符号运算、复杂符号运算中都高于北师大版,两个版本都以简单符号运算的例习题为主,其次为数值运算,这是由向量本身的性质决定的,向量本身既有大小又有方向,所以掌握向量的线性运算是很必要的,在向量的加、减、数乘、数量积、坐标变换中虽然有时候没有涉及字母,但是它仍然属于符号运算.
(4)推理因素的水平比较.
人教A版教材的201个例习题中无推理的占51.8%,简单推理的占37.8%,复杂推理的占10.4%.而在北师大版中无推理的占49.7%,简单推理的占32.8%,复杂推理的占17.4%.如图5所示.
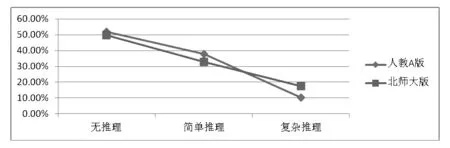
图5 推理因素的水平比较
在图5中可以明显地看出人教A版重点在无推理和简单推理的例习题上面,而北师大版重点在复杂推理上面,并且要高出人教版很多,推理能力作为智力活动的核心因素,是学生学习能力的构成基础,因此两套教材都关注到了学生推理能力的发展.
(5)知识含量因素的水平比较.
在知识含量方面,人教A版教材的201个例习题中1个知识点的占58.7%,2个知识点的占30.8%,而包含3个及3个以上知识点的占10.5%.在北师大版的195个例习题中含1个知识点的占55.4%,2个知识点的占29.2%,3个及3个以上知识点的占15.4%.如图6所示.
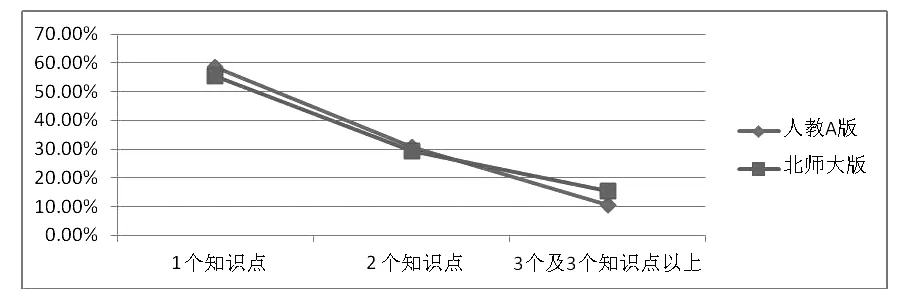
图6 知识含量因素的水平比较
从图6中可以发现两版本包含1个知识点的例习题较多,而在北师大版中3个及3个以上的知识点含量要高于人教A版,由于人教A版教材要适用于好多地区,所以考虑到学生的知识背景,涉及多个知识点的例习题较少.
四、结论与启示
(一)结论
从整体来观察两个版本的例习题编写形式,都是以例子作为引入,然后进行分析,在中间穿插了探究题、思考题,再在每个知识点后安排了相应的习题,这些都符合教师教和学生学的规律.其次每个水平难度因素相当,两版本都注重学生运算能力的培养,有助于提高他们的运算技能.
北师大版教材与向量相关的实例较多,在例习题的情境设计方面更注重向量与其他学科,向量与实际生活的联系,例习题的配图丰富,类型设置较开放自由.注重培养学生的问题意识,将向量知识的学习融入实际活动及问题解决的过程之中,教材通过对问题情境的思考、讨论和理解,引导学生在解决问题的同时掌握相应的向量知识.
人教A版教材向量知识点密度适中,数量上也较多,在“探究式教学”、“信息技术的应用”方面更注重一些,紧跟课标要求,习题的类型比较单一.但是,人教A版较为强调对学生思维的引导,比如,在学习向量的基本运算时,在例题的下面给出“想”的过程,而在学习使用向量来解决问题的时候,更给出了解决问题的基本思路,这可能是人教A版教材的一个亮点.
在两版本教材中,对于平面向量和空间向量的运算性质几乎比较统一地采用先严密后宽疏的模式.即对平面向量的运算性质一般给出较严格的证明,而对空间向量的运算性质则以“类似地可以得到”等描述一笔带过.
(二)启示
(1)例习题各水平难度应尽量平衡.
例习题的设置要确保不同水平的学生在某一学科中共同学习内容的基础性,体现对于不同学生的能力要求,表明练习的内容是真实可测的,提升学业评价.研究表明,两套教材都没有保持5个因素的平衡性,背景因素的难度值相比其他4个因素要小很多,两套教材都特别注重运算,所以例题的选择和编制应与数学内容相结合,充分考虑其特殊性,例如,在向量这一节中要特别注重背景知识,把背景嵌入到例题中,增强学生对向量作用的认识.
(2)适当运用平面向量解决几何问题.
平面向量在高中数学教学内容中有广泛的应用,从本书可以看到利用向量可以得到线段的定比分点公式、平移公式,可以证明正弦定理、余弦定理.在后续的学习中还可看到向量在不等式、函数、几何中广泛应用等.由于应用向量可以将形的推导、证明转化为数的运算,因而向量是解决数学问题的有力工具.向量处理一些几何问题很容易,但由于教材考虑到课时少,控制难度等原因,在编写平面向量时,只要求学生会用两个向量表示其他向量,而没有通过向量运算证明几何问题,任何一门学科都有其自身的知识结构体系,但是作为学校课程在充分反映知识结构的同时也必须十分重视学生的心理发展阶段,合理建立向量教材的螺旋式体系,并逐步应用它们解决几何问题和其他数学问题,将有利于学生对向量概念的正确理解和向量工具的有效掌握.
(3)贴近学生实际,优化知识的呈现方式.
数学应用的广泛性是数学学科的一个重要特征,例习题的选择和编制要注重数学与现实世界的联系,强调问题的背景,要让学生通过数学问题的解决,感觉到数学在现实中有原型,能体会到数学的作用和数学的意义.教材一般是通过提出问题,让学生进行自主探究和思考,并在解决问题的过程中学习向量的有关知识,且基本都是以例题的方式进行讲解和归纳,从而呈现相应的向量内容,例题的讲解很详细,降低了学生学习的难度,呈现的概念和问题大都比较简单和直接,缺乏一些贴近实际又能引发学生进行思考与实践的内容,难以激发学生的学习兴趣.因此,建议改进教材向量知识的呈现形式,创新习题设计.
(4)通过向量的教学,使学生体会到数学各分支之间的广泛联系,进而加深对数学本质的理解.
向量为数学联系提供了重要桥梁.教学中应该努力使学生理解这种联系,并促使他们自觉地利用这种联系去构建和改善自己的认知结构.从数的运算发展到向量运算,使学生对数学的操作对象有了新的认识,而向量运算律与数的运算律之间的高度相似性又使学生领略到了数学中不同运算对象之间在结构化观点下的和谐统一性.将几何问题、三角问题等转化为向量运算特别是坐标形式的向量运算问题,则充分揭示了数学中化归思想的深刻含义,同时也显示了其巨大的威力.因此,通过向量的教学,应使学生从以上各角度加深对数学本质的理解.
1.中华人民共和国教育部.普通高中课程标准试验教科书·数学·必修4(A)版[M].北京:人民教育出版社,2007.
2.中华人民共和国教育部.普通高中课程标准试验教科书·数学·必修4[M].北京:北京师范大学出版社,2007.
3.吕世虎,贾随军,温建红,等著.中学数学课程标准与教材研究[M].北京:高等教育出版社.
4.高文君,鲍建生.中美教材习题的数学认知水平比较[J].数学教育学报,2009(4).
5.汪晓勤.数学文化透视[M].上海:上海科学技术出版社,2013.
6.张奠宙,宋乃庆.数学教育概论(第二版)[M].北京:高等教育出版社,2009.
7.鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望,2002(9).
8.贾随军,吕世虎,李保臻.中国与美国初中数学教材习题的个案比较——以“与三角形有关的角”为例[J].数学通报,2014(9).
9.林丹,胡典顺.中美高中数学教材的习题比较及启示——以PEP教材与UCSMP教材中平面向量章节为例[J].数学教育学报,2014(3).F

