在变式拓展中提升学生的核心素养*
——以《基本不等式的应用》一课为例
☉江苏省无锡市辅仁高级中学 过大维 钱军先
一、问题提出
“掌握数学意味着什么,那就是解题.”解题是数学学习的一个重要环节,在数学学习中一直占据着主导地位,学生对所学的数学知识、数学思想与常用方法的理解和掌握,只有通过解题才能实现和达成.如何通过解题教学,培养学生的数学素养,提升学生的解题能力,是每一位数学教师必须面对和需要着力解决的课题.美国著名数学教育家波利亚说过:“一个专心的认真备课的教师能够拿出一个有意义的但又不复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域.”[1]数学解题不能等同于题海战术,不能就题论题,而要适当地进行变式训练,在变式拓展中揭开数学题目中的内涵和价值,帮助学生树立正确的学科观,培养学生数学学科的核心素养,促使学生触类旁通,举一反三,领悟数学之道,从而有效地提升分析问题和解决问题的能力.下面以《基本不等式的应用》一课中的教学片断为例,谈谈笔者的认识和体会,供大家参考.
二、教学片断
师:我们来看这样的一个问题:x,y>0,x+y=1,求
思考片刻,有两个学生各自提出一种解法:
生1:因为x,y>0,x+y=1≥的最小值为4.
生2:因为x,y所以的最小值为4.
师:两位同学从不同的角度,运用基本不等式求出了最小值,上述过程,有需要完善的地方吗?
生:都没有检查等号成立的条件.
师:很好!运用基本不等式求最值,一定要注意一正、二定、三相等,缺一不可.
经过学生验证,发现虽然生1用了两次基本不等式,但是等号同时成立,所以两个方法都可行,这里笔者特意强调等号成立的条件,为后面打下伏笔.下面笔者趁热打铁,给出变式:
师:如把“x+y=1”改为“x+y=2”(变式1),这个题目还可以解决吗?
很快,有学生用类似生1的方法解决了问题,并且严格地检验了等号成立的条件.但是,当笔者要他们看看有没有类似生2的方法时,学生面露难色了.
师:我们来回顾一下生2的解法,生2在处理的时候,是把“1”换成了题目中的x+y,那现在x+y=2,怎么办,不能代换了?
同学们恍然大悟:把的“1”理解(x+y),其他和生2做法都一样了.
师:难不倒你们吗?再来!条件、结论互换,如果是“因为x,y>=1,求x+y的最小值”呢?(变式2)
经过一段时间的课堂范围讨论,学生意识到变式2的处理依然是法1和法2都可以用.
前面,通过三个类似的问题,使学生对运用基本不等式求最值加深了认识,熟悉了方法,但是鉴于学生的理解还不够,要归纳通性通法,也为了承上启下,笔者进行了小结:
师:原题和变式,我们都用了两种方法,通过比较可以发现,法1都用到了两个基本不等式,恰巧两次基本不等式等号成立条件一致,不等式可以连续取到等号.而法2我们是把已知条件的“1”进行了代换,好处是只需要用一次基本不等式即可.如果给的已知条件不是等于1而为m的话,那在用法2时就再乘一个凑配成右边为1的形式即可.
刚才的两个变式,一个改变了数字,一个改变了条件、结论的顺序,都被同学们轻松地解决了.下面,你们可以自己编制出类似的题目吗?只提一个要求,所有已知或者要求的字母前系数为正.
一开始,学生面面相觑,毕竟以前都是教师出题,学生解题,突然改成了开放性问题,要他们自己出题,他们还是很不适应.但是为了培养学生发现问题和提出问题的能力,课堂上要给学生创造机会.一会儿,一个学生在下面跃跃欲试.
生4:按照前面两个变式的方法,我的题目是:x,y>0,x+2y=5,求的最小值.
师:非常好,我们不仅要学会解决现成的问题,还要善于发现问题和提出问题.同学们还有其他的想法吗?
一石激起千层浪,同学们的积极性被调动起来了,纷纷举手,我根据难易程度,把学生的问题,依次归纳为下面3类:
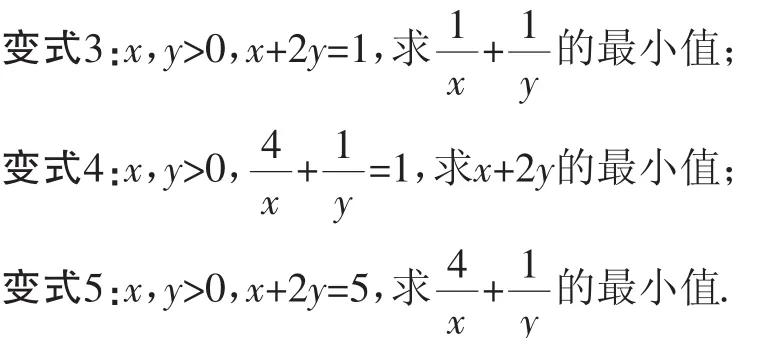
师:非常好,大家提出了很好的问题,怎么解决这些问题呢?先来看变式3吧.
生5:跟法1类似,因为x,y所以
师:大家同意吗?
学生都点头,笔者提问,有没有其他方案?
生6:跟法2类似,用前面的总结得(x+2y
师:怎么两个方法结果不同?
学生纷纷称奇,仔细观察两个方法.
生7:生5的方法用的两次基本不等式等号不是同时成立,所以答案错了!
有了前面的铺垫,这个问题的处理,学生显然得心应手了.紧接着的变式4和变式5,学生也很快发现法1走不通,而法2却没有问题.到了这里,笔者要求学生对本段内容进行小结,学生陷入了沉思.
最后通过讨论,大家对这些题目进行了分析比较,达成如下共识:
(1)运用基本不等式求最值,不能忘记检查等号成立的条件.
(2)形如mx+ny和的两个式子(字母都为正数),知道其中一个是定值的话,另一个就可以求最小值,法1有局限性,所以从通法的角度说,法2显然是常规方法.
师:非常好,最后笔者留下了两个思考题:
①x∈(0,1),求的最小值.
②如果形如mx+ny和的两个式子,其中字母m、n、p、q有负数,该如何处理,还能不能解决呢?
三、几点思考
变式训练是一种揭示数学本质的思维过程,作为一种教学常用的手段,它能够基于一个问题进行相应的拓展和扩充,培养学生的发散思维能力和发现问题、解决问题的能力,避免同一个问题反复练、天天练,将学生从题海中解脱出来,能在不断变化的背景下辨析正误、深化理解,内化知识、形成网络,提升数学思维能力、升华数学思想方法,培养学生的应变能力、创新能力,从而使解题思路从“特殊到一般”的质的飞跃.[2]在解题教学中,要善于运用变式拓展,从而有效地提高教学的效益.
1.一题多解,在探索发现中拓宽解题的思路
对于一个数学问题,因思考的角度不同,可得到多种不同的思路.解题教学时,启发学生从不同的角度进行思考,用不同的方法建立模型,让学生去比较,在思考比较的过程中,使学生感受从不同的角度解决问题,用不同的模型理解问题的优劣性.不同的解题方法对于学生来说都是一种创新思考的机会,学生的思维不会被题型所局限,有助于学生更深层次地理解题型,能够很好地培养学生运用数学知识的能力.
为了拓展和发散学生的解题思维,我们需要在平时的高中数学教学过程中,不失时机地来引导学生共同开展“一题多解”的训练,帮助学生更进一步地了解和认识相应的数学知识,深化学生对于数学知识的理解和认识,以便借此来促使学生进行全方位、多角度的思考,拓宽学生的解题思路,拓展学生的思维空间,提高学生思维的深刻性和广阔性.
2.一题多变,在变式引申中发展学生的思维
数学课堂教学中,往往一节课就学习一个知识点.要让学生能够将所学习的知识掌握好,就要求我们在教学时要吃透教材,将知识向纵深处挖掘.一题多变,就是为做到这一点而首选的一种好的操作方法.由课本上的例题或习题设计变式训练题,这样不仅能使学生学会基础知识,还能提高学生的应变能力,拓展学生的思维空间.而不需给学生布置太多的课外作业来增加学生的负担,因为作业多了只会加剧学生的厌学情绪,变式训练起到了让学生有章可循、层层推进、逐步提高的作用.
教师应将讲解的例题进行适度的推广和变通,将题目中的具体条件亦或是解题的结论作为已知条件进行再次转变,从而更全面、深人地探究问题本质的变与不变的内在联系.使学生开动脑筋根据改变的情况进行主动、积极的思考,迅速找出针对问题解决的方法,避免呆滞和僵化的现象发生.拓展学生学习领域的同时刺激学生对知识的探索与发现的求知欲望,提升学生对知识的学习欲望和发现精神.
3.多题一解,在本质揭示中深化学生的理解
学生的学习过程就是在头脑中寻找适合该题目的解题途径及方法.许多同学在不同类型的题目中无法选择合适的方法解决问题,最根本的原因在于没有归纳整理出一套有价值的规律及体系.这就要求教师在教知识的过程中,注重用一种方法解决多种题型,将表面上变换不同的条件,找出其本质相同的要素,从而更有效地解决问题,通过事物的本质揭示事物的整体规律,实现变厚为薄的教学目的,帮助学生学习规律总结的方法,以及培养学生自主学习的能力.
“多题一解”的变式教学,本质上来说就是,从看上去题目不太相同,问题要求不大相同的题目中,梳理出它们之间存在的一定的内在联系.所有的数学问题都是依据一个或多个数学知识组织成的,而数学这一学科又是所有的学科中,知识的联系性、逻辑性最强的一门学科,也就意味着数学学科的所有知识存在着千丝万缕的联系.教师就应该在数学教学中帮助学生打开思维,从“题海”中发现一般性的规律,发现一类题型的共性,从而找到这类题型的解题思路,进而提高解题的速度,最终帮助学生理解知识的内涵和本质属性,准确地把握数学学科的规律.
4.角色互换,在问题提出中发展学生的素养
爱因斯坦说过:“提出一个问题往往比解决一个问题更重要.”科学发现过程中的第一个重要环节是发现问题.因此,引导和鼓励学生提出问题、发现问题是很有意义的.即使经过检验发现这个问题是错误的,但对学生思维的训练也是有益的.如何让学生学会在从变化中找出不变的本质呢?一个最有效的方法,就是教师要充分调动学生学习的积极性,让学生主动去变式.在教学中,教师要善于抓住适当的时机,巧妙地运用角色互换的方法,主动地引导、启发学生提出问题,让学生也学会变题并去探索分析综合,进而有效地提高分析问题和解决问题的能力.
学生是学习过程中的重要主体,从他们的思维特征和生理、心理特点来看,每个学生都有探索与创造的潜能,关键是如何激发他们学习的兴趣、动机和求知欲.[3]运用变式教学不仅能使学生对所学内容与练习保持浓厚的兴趣,而且还创设了学生共同参与的环节,并使学生在亲自参与的实践中去认识问题的本质,体验灵活运用知识与技能解决问题的乐趣,从中促进智力的发展和能力的提升.
教学实践表明,大量单一的、重复性的机械性练习,达到的效果不是“生巧”,而是“生厌”,它不仅对学生知识和技能的掌握无所裨益,而且还会使学生逐步丧失学习的兴趣,这正是“题海战术”的最大弊端.而变式教学是使学生在亲自参与中展示知识发展过程,并在知识的运用过程中让学生体验到解决问题的快乐,从中进一步激发参与的积极性,并在积极主动的思考、探索中发现问题,抓住本质、把握其规律性,从而将所学知识纳入自己已有的知识系统,获得更深刻的理解,并逐步形成解决问题的能力素质,培养创造性思维能力.因此,我们要深入研究变式训练思想的含义,将变式训练运用到高中数学解题实际中,以提高学生解题时的应变能力,拓展学生的思维,提升学生的数学素养.
1.南小康.一道课本例题的改造和延伸[J].中学数学研究(华南师范大学版),2016(02).
2.李红光.变式挖掘,借题发挥——以一道课本例习变式构造为例[J].中学数学(下),2017(11).
3.苏振新.基于数学核心素养的数学教学——以数系的扩充为例[J].中学数学(下),2017(9).F

