巧计反例冲突,促进知识的深刻理解—以概率中“等可能性”教学为例

湖北省三峡职业技术学院(100029) 覃文平

小颖为学校联欢会设计了一个“配紫色”游戏:下图(图1)是两个可以自由转动的转盘,每个转盘被分成几个扇形.游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.

小亮则先把转盘A的红色区域等分成2份,分别记作“红色1”“红色2”(图2),然后制作了下表,据此求出游戏者获胜的概率也是

师:你认为谁做得对?说说你的理由.

(学生小组讨论)

生1:小亮做的对;因为在利用树状图或列表的方法求概率时,各种结果出现的可能性必须相同.

生2:小颖和小亮两人都对;因为红色区域分或不分结果都一样.

(对于生1,老师予以肯定)

师:小颖和小亮的结果会不会仅仅是巧合呢?怎样证明!

生:······

师:其实举反例可以证明这仅仅是一个巧合.

师:大家看下面这个例子.

反例:求下图(图3)配成紫色的概率.

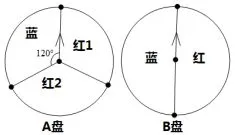
图3

师:在用树状图和列表的方法求概率时,应注意各种结果出现的可能性必须相同.

师:请同学们完成下面练习······

案例评析

在学习概率的过程中,对于“等可能性”概念的理解至关重要.整个学习活动,既需要教师的精心组织,又需要学生的自己感悟.本案例具有如下一些特点,值得考虑:

第一,整个教学过程言简意赅,且改变了重结论轻过程的传统教学模式.

第二,学生可能一下子就能接受“等可能性”这个结论,但能完全理解的极少.如果没有继续的反例演示,学生很可能就是一知半解.

第三,反例的选择恰到好处,学生很容易就能算出不同情况的概率,且很容易知道正确的概率是多少,从而达到教学效果.

[1]李铁安.《案例式解读》.教育科学出版社

[2]马复.《初二数学》.北京师范大学出版社