树状结构稳定承载力研究★
张 佳 宁
(辽宁工程技术大学土木工程学院,辽宁 阜新 123000)
1 概述
树状结构是德国建筑师Frei Otto于20世纪60年代基于仿生学概念提出的一种新型仿生结构形式,由于其良好的受力性能和美观的结构外形在广大的设计师和工程师中得到了广泛的关注[1-7]。树状结构的传力特点是将作用于结构顶部大范围荷载沿着分支传递到最低级的分支,形成力流,逐级向下传递,最后汇聚到树干,进而传递到地面上的一点。具有较高的结构效率[8],从而被广泛的应用于大型建筑中,如图1所示。由于其美观的结构外形,树状结构往往会成为地标性建筑[1,5]。

通过以树状结构作为支撑的火车站,机场等一些大跨度空间结构,支撑起来的屋顶结构的刚度要大大超过了树状结构自身的刚度。而且树状结构像自然界中的树一样向外扩展,直接的使自身所要承受的屋顶跨度和挠度减小,这样就可以忽略屋顶结构产生的变形,假定屋顶刚度远大于树状结构自身的刚度,基于这一假定,屋顶除了会向下传递荷载外,树状结构还会遭受到水平力的作用,而且树状结构自身受力比较均匀,当结构遭受的荷载或者外力到达一定值时,继续施加荷载,结构的平衡状态就会发生非常大的改变,这时所出现的现象就称之为结构失稳或者结构屈曲。
在压力的作用下,构件会出现失稳现象。所以,不论是整体结构还是单一的构件都需要考虑结构的稳定性问题,结构的稳定性是树状结构整体受力性能至关重要的因素。本文作者[9]已对树状结构的找形和优化进行了研究,但还未分析树状结构的失稳特征和稳定承载力[15]。本文针对于树状结构整体稳定性分析进行了系统的研究与阐述,其中主要分为两部分:分别对树状结构找形前和找形后进行特征值屈曲分析和非线性屈曲分析,借此来验证找形对于树状结构稳定性的影响。
2 模型建立
2.1 几何参数
树状结构的组成部分可以根据它们相对于树干位置进行分类,如图2所示。从树干上分出的支条被定义为一级分支,从一级分支构件分出被划分为二级分支。属于第i级分支的构件分出被划分为第(i+1)级分支。树状结构连接节点可以根据每级分支的数量进行分类。不同连接类型的示意图如图3所示。各级分支长度如表1所示。其中Si表示树状结构类型。


表1 不同情况下树状结构各级分支计算长度

m
如图4所示为树状结构几何参数,H0指树状结构树干高度;Hi为第i级分支的高度;参数li指的是结构轴向上第i级分支的长度;参数Ф指的是一个分支与其更高级分支在轴向之间的夹角。各级树状结构分支夹角如表2所示。树状结构截面参数见表3。

表2 不同情况下树状结构各级分支计算角度

(°)

表3 树状结构截面参数
2.2 有限元模型及边界条件
通过通用有限元软件ANSYS建立树状结构,采用双单元法[10-12]建立简化模型,这种方法假定树状结构的每一个构件由两个单元组成,即只有抗弯刚度的梁单元和没有抗弯刚度的梁单元。杆单元的横截面积远大于梁单元,梁单元的抗弯刚度远大于杆单元。在找形分析中,降低抗弯刚度以减小抗弯刚度的影响,因此梁单元可以更好的模拟丝线模型[13,14]。基于逆吊法[3-5]的基本思想在上方施加指定的载荷。如图5所示为双单元法建立的五级6-4-4-2-2树状结构简化模型。
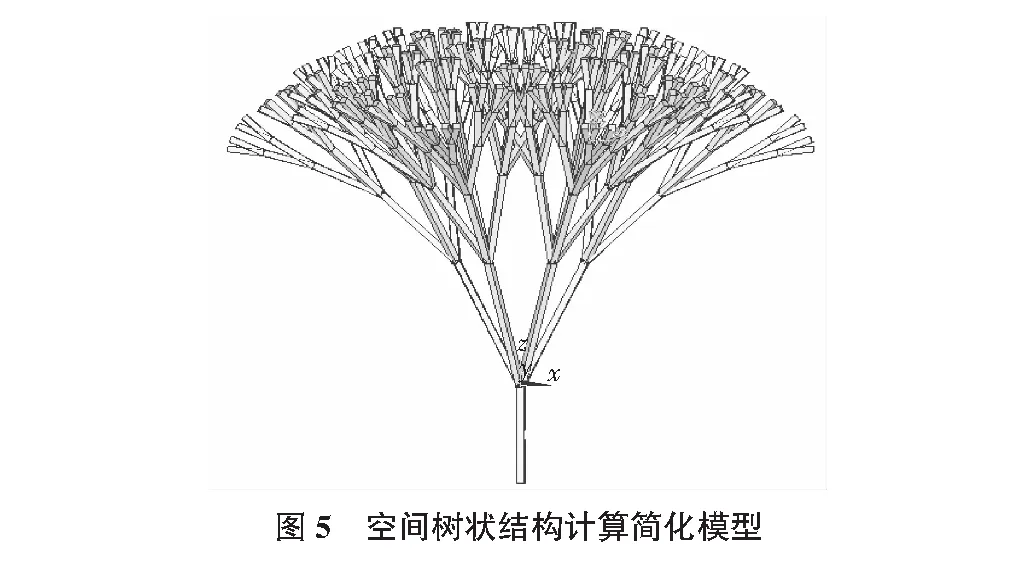
根据连接形式的不同,一般屋架结构与下部支撑结构采用刚接或者铰接,本文在考虑树状结构的基本受力状态,采用铰接的形式,树干底部采用固接形式,结构的顶层各个节点竖直方向施加5 kN的荷载,如图6所示。
2.3 找形分析
赵中伟等[7]提出并利用双单元法模拟树状结构。在本文中,上端在x和y方向上的平移度是固定的,树干部位的平移程度均固定。在找形分析中只有水平坐标发生变化。在数值分析中,根据逆吊法的基本概念,向上施加指定载荷。然后进行模拟分析,得到节点位移。提取所有节点的水平位移,将水平位移与初始节点坐标求和得出新的节点坐标,通过新的节点坐标建立树状结构的双单元数值模型,重新计算,通过树状结构找形分析的迭代程序,直到节点的最大位移小于允许误差为止。这样通过多次迭代,所有构件均只受轴力的作用,弯矩较小可以忽略不计。

3 非线性屈曲分析
为了进一步探讨树状结构的结构缺陷和结构失稳机理,对树状结构进行非线性屈曲分析。其中考虑几何非线性对于树状结构的整体稳定性能的影响。目前非线屈曲分析的应用已经很成熟了。
在固体力学的问题中,所有现象都是非线性的。然而在工程项目中遇见的很多工程问题,近似地使用线性理论来处理是简单切实可行,并且符合工程中的精度要求。
结构的非线性分析问题可以分为三大类:几何非线性问题,材料非线性问题,状态非线性问题。一般来说,结构非线性问题并不是单纯的某一类问题,可能需要同时考虑共同作用的非线性问题,其中包括三种非线性问题并存的情况,这些问题都可以用ANSYS来解决。
非线性方程一般采用Newton-Raphon方法,这是求解非线性方程的线性化方法,对于树状结构来说,应考虑的是几何非线性问题,结构的平衡方程为:
[K({u})]{u}={F}
(1)
写成NR法迭代公式为:
[KT({u}n)]{Δu}n+1={F}-{F}n
(2)
{u}n+1={u}n+{Δu}n+1
(3)
本节对树状结构进行非线性屈曲分析时,在进行非线性屈曲分析过程中,根据结构在特征值屈曲分析过程中得到的一阶失稳模态施加初始缺陷。材料的非线性考虑使用理想状态下的弹塑性模型。在进入求解状态时,采用弧长法对树状结构进行非线性整体分析。
3.1 树状结构找形前非线性分析
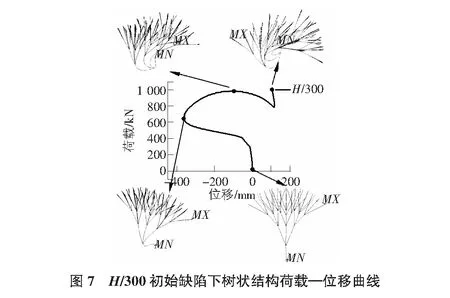
为了探究在树状结构非线性屈曲分析找形对于树状结构稳定性的影响,先对于5-6-4-4-2-2分支形式的树状结构进行非线性分析,选取施加不同程度的初始缺陷大小,研究在不同参数状态下的树状结构失稳形态和失稳过程。如图7所示为首先施加H/300的初始缺陷。
如图7所示,选取树干部位与一级分支连接处的7031节点,给出了在H/300的初始缺陷下树状结构的荷载—位移曲线,可以清晰的看出,在几何非线性条件下,树状结构的荷载—位移曲线非常圆滑,在结构失稳变形后,尤其是发生大变形时,树状结构在一定范围内还可以承担荷载,在结构达到负向的最大位移后,又趋向正向位移,此时树干受力形式从受压失稳转向受拉失稳。同时,从图中可以清晰的发现,结构失稳已经从树干失稳转向了树状结构外部高级分支的失稳。通过树状结构失稳变形图,可以发现,在考虑几何非线性条件下树状结构的失稳破坏形式和特征值屈曲分析中一阶模态失稳破坏比较相似,最大位移处也发生在最高级分支顶部边缘处。
3.2 树状结构找形后非线性分析
对树状结构进行找形,探究找形对树状结构非线性屈曲分析的影响,在找形后施加相同条件的初始缺陷,研究找形后树状结构失稳形态和失稳过程。施加H/300的初始缺陷。
如图8可以清晰的看到在H/300的初始缺陷下找形后树状结构的荷载—位移曲线,在几何非线性条件下,树状结构的荷载—位移曲线非常圆滑,在结构失稳变形后,尤其是发生大变形时,树状结构在一定范围内还可以承担荷载,在结构达到负向的最大位移后,树状结构从局部受压转向局部受拉。可以明显看出树状结构树干部位变形明显,和找形前进行对比,分支部位变形较小。
通过树状结构失稳变形图,可以得出一阶模态失稳破坏变形图,数据表明,树状结构的最大位移处发生在树根部位与最高级分支顶部边缘处。
通过对比研究,结果表明,树状结构的非线性失稳模态,一般不受初始缺陷的影响。

4 结语
本文对找形前后的树状结构进行了稳定特性分析。以双单元法建立的树状结构数值模型为基础,提出了树状结构的非线性屈曲分析。
1)结果显示找形对于树状结构的稳定性并没有太大的影响,在找形前后并没有明显改变树状结构失稳形态。在给定荷载下,大跨度树状结构的各个分支因轴力或者轴力与弯矩的共同作用,结构发生的失稳位移更加明显。
2)基于几何非线性对树状结构的整体稳定性进行了非线性分析。找形前树状结构受初始缺陷影响不大,找形后树状结构在失稳后仍能在一定范围内承担荷载。
3)通过树状结构整体稳定性分析发现,树状结构受树干,一级分支以及结构跨度对结构的稳定性起着明显的作用,设计时可以通过增加树干和一级分支刚度,减小结构跨度等方法来提高树状结构稳定性。

