咬文嚼字 明辨概率

范 斌

学习语文需要咬文嚼字，学习数学也需要咬文嚼字。概率问题，看上去好像很简单，其实并非如此，如不细细审题，咬文嚼字，稍不留神，便会出错。

例1甲、乙、丙三名同学站成一排进行毕业合影留念，求甲、乙两人相邻的概率。

【错解】用树状图分析如下：

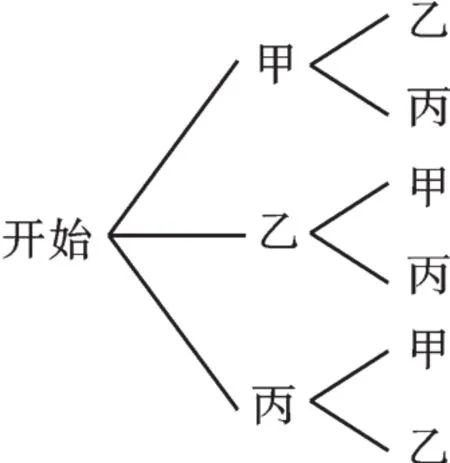
∵共有6种等可能的结果，甲、乙两人相邻有2种情况，∴P（甲、乙两人相邻）=

【分析】树状图画出了甲、乙、丙中两人站的位置，留下的一个位置给剩下的第三人。当你完整列出三人站的位置图时会发现，共有4种站法使甲、乙两人相邻。其实本题也可看成是三个层次的排序站位问题。

【正解】用树状图分析如下：

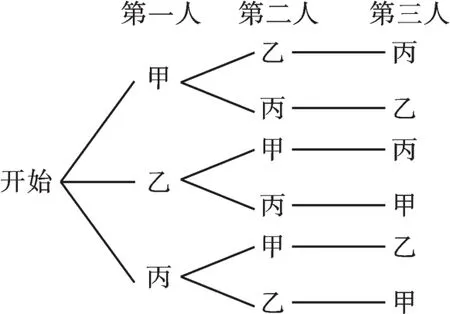
∵共有6种等可能的结果，其中甲、乙两人恰好相邻有4种情况，∴P（甲、乙两人相邻）

例2某校组织学生参观航天展览，甲、乙、丙、丁四位同学随机分成两组乘车。用列表法（或树状图法）求甲、乙分在同一组的概率。

【错解】根据题意画树状图如下：

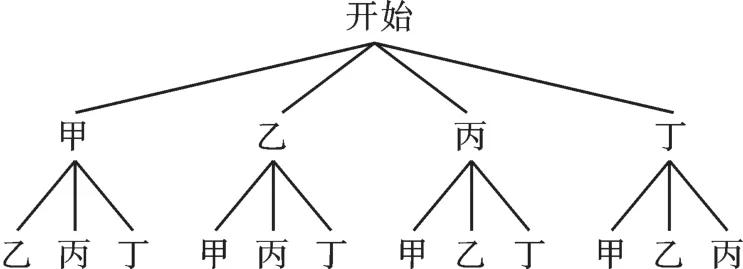
∵共有12种等可能的结果，甲、乙分在同一组的有2种情况，∴P（甲、乙分在同一组）=

【分析】当丙、丁，丁、丙在一组，也意味着甲、乙两人在另一组，错解恰恰遗漏了这种情况，导致错误。

【正解】根据题意画树状图如下：

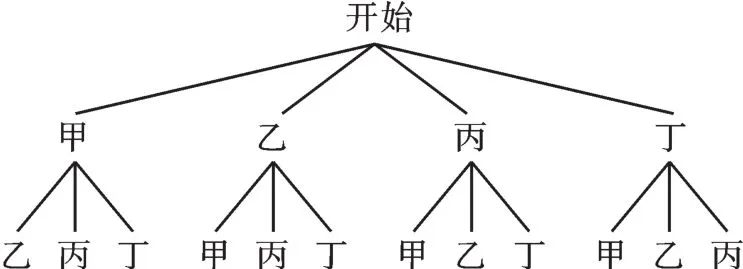
∵共有12种等可能的结果，其中甲、乙分在同一组的有4种情况，∴P（甲、乙分在同一组）

【点评】我们在用树状图法求概率时，切不可画出树状图后便急不可待地忙于求概率，一定要咬文嚼字，仔细审题，读懂题目中每一句的含义，小心谨慎地不重不漏地列出所有等可能的结果。