一类无限可能问题的解法

王华钧

【原题呈现】苏科版九（上）第129页练习1：A、B两地之间的电缆有一处断点，断点出现在电缆的各个位置的可能性相同吗？

【解析】断点会出现在A、B两地之间电缆的任何一处（有无限多个可能的结果）；出现在电缆的各个位置的可能性相同。

【原题呈现】苏科版九（上）第142页习题4.3第2题：按下列要求设计一个转盘：任意转动转盘1次，当转盘停止转动时，指针落在红色区域的概率为。

【解析】只要涂有红色的扇形面积占整个转盘面积的即可，答案不唯一。

【点评】练习中断点出现的位置有无限多个可能的结果，习题中转盘指针停止的位置也有无数多种可能的结果，而且它们都具有等可能性。无限的问题如何处理？转盘问题的解决方案告诉我们：化无限为有限。对于转盘，教材采用面积转换：一般地，设试验结果落在某个区域S中每一点的机会均等，如果把“试验结果落在S中的一个小区域M中”记为事件A，那么P（A）

【变式1】小明将如图所示的转盘分成n（n是正整数）个扇形，并使得各个扇形的面积都相等，然后他在这些扇形区域内分别标注连续偶数数字2，4，6，…，2n（每个区域内标注1个数字，且各区域内标注的数字互不相同），转动转盘1次，当转盘停止转动时，若事件“指针所落区域标注的数字大于8”的概率是，则n的取值为（ ）。

A.36 B.30 C.24 D.18

【解析】∵事件“指针所落区域标注的数字大于8”的概率是，不大于8的偶数数字只有解得n=24。答案：C。

【变式2】正方形ABCD的边长为2，以各边为直径在正方形内画半圆，得到如图所示阴影部分，若随机向正方形ABCD内投一粒米，则米粒落在阴影部分的概率为（ ）。

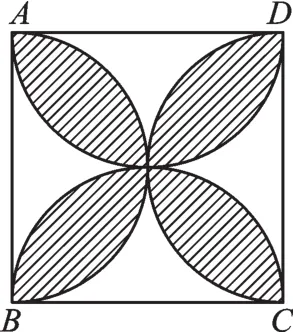
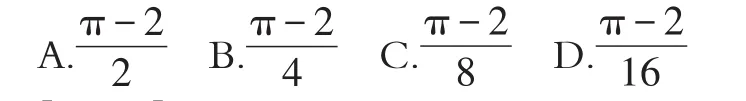
【解析】因为正方形ABCD的面积为4，阴影部分的面积为四个半圆的面积与正方形ABCD的面积之差，即-4=2π-4，根据前面P（A），有P（米粒落在阴影部分）=答案：A。