例析“模式图识别”对数学教学的启示

浙江省嘉兴市塘汇实验学校(314003) 姚建新

从每年的中考数学试题[1]中可以明显看出,中考重视对基础知识、基本技能和通性通法的考查,一方面,数学是关于数与形的科学,数与形的有机结合是数学解题的基本思想;另一方面,数学是关于模式的科学,这反映了在数学解题时,需要进行“模式识别”,需要构建标准的模型.

由于“具有某些规律性和普遍意义的常规解题模式和常用的数学思想方法”更是考查学生数学能力的知识点,所以,我们在日常教学中,关键不是让学生记住结论,而是要让他们经历探究的过程,感受数学的研究方法,促进数学能力的提高,只有在运用通性通法进行不断变式的演练中,才能提高学生对数学的理解和解题能力.通过变式教学,教师有意识、有目的地引导学生从“变”的现象中探究“不变”的本质规律,帮助学生从多角度理解知识,并掌握数学知识中蕴含的数学思想和方法,从而达到灵活运用知识的目的.

一、模式图的确立

如图1,已知点P是抛物线上的任意一点,记点P到x轴距离为d1,点P与点F(0,2)的距离为d2,求证:d1=d2.

图1

证明 因为P为抛物线上一点,所以设则P到x轴距离到点F(0,2)的距离所以d1=d2.

此题的证明并不难,为了下文的说明方便,我们把图1记为“模式图”.

二、模式图的应用

例1如图2,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,D、E在x轴上,CF交y轴于点B(0,2),且其面积为8.

(1)求此抛物线的解析式;

(2)如图3,若P点为抛物线上不同于A的一点,连接PB并延长交抛物线于点Q,过点P、Q分别作x轴的垂线,垂足分别为S、R.

①求证:PB=PS;②判断△SBR的形状;

③探索:在线段SR上是否存在点M,使以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似?

图2

图3

简解(1)因为B(0,2),所以OB=2,因为矩形CDEF面积为8,所以CF=4,所以C(-2,2).又A(0,1),根据题意可设抛物线解析式为y=ax2+c,则,得所以抛物线解析式为

(2)如图4,①参见“模式图”证明;

②根据①得PB=PS,同理可知BQ=QR,所以∠1=∠2,又因为∠1=∠3,所以∠2=∠3;同理∠SBP=∠5,所以 2∠5+2∠3=180°,即∠5+∠3=90°,所以∠SBR=90°,所以△SBR为直角三角形.

图4

图5

图6

③方法一:如图5,设PS=b,QR=c,则PQ=b+c,可计算得假设存在点M,并设MS=x,则因为∠PSM=∠QRM=90°,所以若△PSM～△MRQ,可求得所以M为SR的中点;若△PSM～△QRM,则有得(平行线分线段成比例定理),所以M点为原点O.

方法二:如图6,若以P、S、M为顶点的三角形与以Q、M、R为顶点的三角形相似,则有△PSM～△MRQ和△PSM～△QRM两种情况.当△PSM～△MRQ时,由直角三角形两锐角互余性质,知∠PMS+∠QMR=90°,所以∠PMQ=90°.取PQ中点N,连结MN,则MN=所以MN为直角梯形SRQP的中位线,得点M为SR的中点;当△PSM～△QRM时,由方法一知即M点与O点重合,得点M为原点O.综上所述,当点M为SR的中点时,△PSM～△MRQ;当点M为原点O时,△PSM～△QRM.

例2已知,在平面直角坐标系xOy中,点A的坐标为(0,2),点P(m,n)是抛物线上的一个动点.

(1)如图 7,过动点P作PB⊥x轴,垂足为B,连接PA,请通过测量或计算,比较PA与PB的大小关系:PA___PB(直接填写“＞”、“＜”或“=”,不需解题过程);

(2)请利用(1)的结论解决下列问题:

①如图8,已知C(2,5),连接PC, 探究:AP+PC是否存在最小值?

②如图9,过动点P和原点O作直线交抛物线于另一点D,若AP=2AD,求直线OP的解析式.

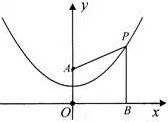
图7

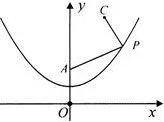
图8

图9

解析第(1)小题的证明同“模式图”.

第(2)小题,对于问题①,我们认识到PA可以“转移”到PB,所以求“AP+PC的最小值”,即求“CP+PB”的最小值,如图10,过点C作CE⊥x轴,垂足为E,交抛物线于点H,因为C(2,5),得CE=5,所以AP+PC的最小值为5,且P(2,2).

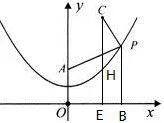
图10

图11

对于问题②,继续利用(1)的结论,如图11,将AP、AD分别“转移”到PB、DF位置,其中PB⊥x轴,DF⊥x轴,则有PB=2DF,马上联想到“相似三角形”知识.设直线OP的解析式为y=kx,得所以因为点D在抛物线上,所以解得所以故直线OP的解析式为或

思考对于问题②,如果作D关于y轴的对称点D′,则D′、A、P是否在一直线上?

变式1如图12,已知:直线l∶y=-2,抛物线y=ax2+bx+c的对称轴是y轴,且经过点(0,-1),(2,0).

(1)求该抛物线的解析式;

(2)点P是抛物线上任意一点,过点P作直线l的垂线,垂足为Q,求证:PO=PQ;

(3)请你参考(2)中结论解决下列问题:

①如图13,过原点O作任意直线AB,交抛物线y=ax2+bx+c于点A、B,分别过A、B两点作直线l的垂线,垂足分别是点M、N,连结ON、OM,求证:ON⊥OM;

②如图14,已知点D(1,1),试探究在该抛物线上是否存在点F,使得FD+FO取得最小值?

图12

图13

图14

简析(1)由抛物线y=ax2+bx+c的对称轴是y轴,就可以得出得b=0,所以y=ax2+c,由待定系数法可以求出抛物线的解析式为

(2)证明参见模式图;

(3)①参见图4的证明;

例3如图15,二次函数图象的顶点在原点O,且经过点点F(0,1)在y轴上,直线y=-1与y轴交于点H.

(1)求二次函数的解析式;

图15

(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP;

(3)当△FPM是等边三角形时,求P点的坐标.

简析对问题(1),参照图2法可得

对问题(2),参照图4法可证;

思考对于问题(3),如果△FPM是等腰三角形呢?

变式2已知抛物线y=ax2+bx+c,当x=0时,有最小值为1;且在直线y=2上截得的线段长为4.

(1)求此抛物线的解析式;

(2)如图16,点A是抛物线与y轴的交点,点P为抛物线上不同于A的一点,已知F(0,2),连接PF并延长交抛物线于点Q,过点P、Q分别作x轴的垂线,垂足分别为M、N,以PQ为直径的⊙D与y轴的交点为C、B.

图16

①求证:PM=PF;②求证:⊙D与x轴相切;

③探索:OM·ON的值是否为定值?

④若OC·OB=1,求四边形PQNM的面积和直线PQ对应的函数解析式.

解(1)因为当x=0时,有最小值为1,所以解得b=0,c=1,所以抛物线关于y轴对称,因为抛物线在直线y=2上截得的线段长为4,所以抛物线经过点(-2,2)与(2,2),得4a+1=2,解得所以此抛物线的解析式为

(2)①参见模式图可证明;

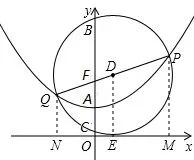
图17

图18

三、模式图识别对教学的启示

1、《数学课程标准》[2]在几何方面的学习目标是要求学生“能从较复杂的图形中分解出基本的图形,并能分析其中的基本元素及其关系,利用直观来进行思考”.本文中所指的“模式图”是从重要的例题和习题所对应的图形中提炼出来的经验型基本图,我们说,兴趣来自思维,思维来自惊奇和疑问,而能诱使学生自觉地、刻苦地从事学习劳动的一种最强有力的刺激物,就是赋予他的脑力劳动以人情味,所以重视例、习题的教学,对于优化学生的认知结构,发展学生的数学思维能力都是大有好处的.

2、从学习论的角度来看,信息加工论认为:不能仅仅考虑到刺激的特征,还要关注学习者已有的信息和认知图式;强调要把复杂问题转化为简单的基本图形的问题,把陌生问题转化为熟知的基本图形的问题.像本文所提到的许多几何内容的练习都有共性之处,如果能够把其中最有共性、最本质的基本元素提炼出来,这会给解决问题带来便捷.所以教师在日常教学中,应恰当使用信息技术,改善学生的学习方式,引导学生借助信息技术学习有关数学内容,探索、研究一些有意义、有价值的数学问题.

3、教育家布鲁姆[3]曾说:“人们获得的知识如果没有完满的结构把它们联系在一起,那是一种多半被遗忘的知识,一串不连贯的论据在记忆中仅有短促的可怜的寿命.”许多学生学习数学的短板显示他们不能“复合”数学知识点,所以一方面,我们在课堂上要指导学生在审题(读图)后还需要层层深入思考,尽可能多的想到或找到“模式图”或与“题目条件”相关联的知识;另一方面,随着现代认知心理学的发生和发展,图式理论已不断得以丰富和完善,并被广泛用于阅读、理解等心理过程的研究.

4、从一些最基础、最基本、最简单的几何基本图形教学入手,尽量直观化,是图形概念接轨学生感知的重要途径,可以促使学生在头脑中快速形成各种基础知识的表象图形,有利于培养学生的组合与创新,以及从复杂问题中去分析、解决问题的能力.因为学生总是需要根据特定学习任务对他们意味着什么而投入到相应的学习活动中去的,不同的学习目标必然导致学习的客观要求与学生的主观意愿之间的不同相互作用.

5、成功的教学不仅需要热情,更需要“智慧”,重视基本图形教学,可以有效扩大记忆容量.有位哲人说过:“经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另一只眼睛就能看到纸背面的话.”我们对数学知识的学习如果离开了对其结构的认识和理解,那么就很难深刻的领会,更无法灵活的运用知识解决问题,这种支离破碎的知识是没有生命力的,相反,如果我们把数学知识放在特定的知识结构中去考察,搞清它的前因后果,来龙去脉,这样组织过的知识不仅容易理解,也容易巩固,更为人们的记忆提供了便利.

6、当前,中考命题的指导思想是突出数学基础知识、基本技能和基本思想方法的考查,数形结合思想突出了直观思维,是对抽象思维的有力解释.课堂上,我们应尽可能给学生以数学的基本思想方法为指引,学会研究基本图形,并分析基本图形的特征,归纳基本图形的性质与判定,因为课堂是向未知方向挺进的旅程,随时都有可能发现意外的通道和美丽的图景,而不是一切都必须遵循固定线路而没有激情的行程.

[1]12999数学网,2014、2015、2016、2017年全国各地中考数学试卷[J],中考专栏.

[2]《义务教育数学课程标准(2011年版)》[S],人民教育出版社,www.pep.com.cn.

[3]杰罗姆·西摩·布鲁纳,教育过程[M],文化教育出版社,1960年.