复数概念教学新设计
贵州省毕节第一中学(551700) 李敏瑜
华南师范大学数学科学学院(510631) 何嘉颖
教材人教A版普通高中数学选修2-2第三章第一节
课时安排第1课时
教学对象高二(下)学生
教材分析
本节内容涉及到了数系扩充的过程、复数概念、复数的代数形式以及复数集与其它数集的关系,这是学生学习复数的几何意义及其四则运算的基础.教材通过类比自然数系到实数系的扩充过程,为了使方程x2+1=0有解,直接引出复数的概念.这种引入方式看似简洁,但与数学史不符,而且对学生而言太突兀,难以接受.学生也不了解复数是如何被发现的,虚数单位是如何被定义的,也不可能体会到引入复数的必要性以及复数的应用价值.
学情分析
认知基础:
学生已学习了正整数集、整数集、有理数集、实数集以及相应的数的运算法则和运算律,有了数系扩充的一些经验;学生已掌握一元一次方程、二元一次方程的求解方法以及方程的解的概念,了解乘方运算与开方运算的互逆关系、数学的逻辑用语以及推理与证明的相关知识,这些都是引入复数概念的基础.
认知障碍:
①缺乏从整体上重新审视数系发展的过程,不知道数系是如何扩充的以及它与生产生活及方程求解之间的关系;
②对方程无实数解的认知不准确;
③承认负数可以开平方.
教学目标
知识与技能
①理解复数的基本概念(虚数单位、纯虚数、虚数等);
②掌握复数的代数形式;
③了解复数集与其它数集之间的集合关系以及代数形式上的关系;
过程与方法
①经历观察发现、猜想并形成复数概念的过程,领悟复数发现的探索思路,学习数系扩充的思想;
情感态度价值观
①感受数系扩充与生产生活之间的关系、与方程求解之间的关系;
②感受引入复数的必要性;
③体会复数的产生是源于生活中数学方程求解的需要,以及感受人类理性思维的作用.
教学重点感受数系扩充、生产生活、方程求解三者之间的联系;理解复数的概念;掌握复数的代数形式.
教学难点复数概念引入的必要性与合理性.
教学关键从方程求解入手,用符合学生认知的演绎推理方法导出复数引入的必要性.
教学方法问题驱动,引导探究.
教学手段板书、PPT.
教学流程

教学过程设计
(一)问题引入
(1)新课引入:
提问:1、数以及数集的概念是如何产生和发展的?
2、除了实数,还有没有其它数;是否存在比实数集范围更大的数集?
活动1:从数学史和已学知识分别回顾数的发展过程
从数学史回顾数的发展过程:

从已学知识来回顾数的发展过程:
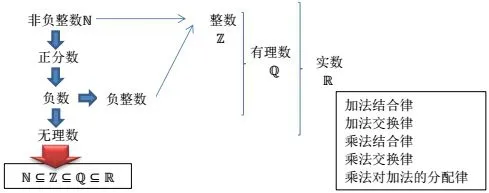
(2)得到结论:我们学习数的过程和历史上数的发展过程大同小异,数不断发展的过程称为数系的扩充.此外,从数学与生活看:数的发展与生产生活有关;从数学世界看:数的发展与方程求解有关.
(3)问题引导:已发现数的发展与方程求解相关,故引导学生继续从方程求解入手探索数的进一步发展.
设计意图通过回顾数学史以及学生所学知识中数的发展过程,使学生体会到现实生活对数学发展的推动作用以及方程与数的发展的联系,从而使学生对数系扩充形成整体的映像,同时,激发学生继续尝试从方程出发探索数的发展的动力.
(二)探究发现
(1)特殊入手:让学生用旧知求解具体方程-7x+6=0、x2-7x+6=0、x3-7x+6=0,回忆求解方程的方法.
学情预设生:上述三个方程的解分别是或x=6,x=1或x=2或x=-3.
(2)归纳方程求解的一般方法:出示上述方程的解,给出一次、二次方程的一般解法.并询问学生,他们求解方程、x3-7x+6=0的方法,从而得到求解一元三次方程的原始方法—赋值法.
学情预设生:观察到把1代入方程、x3-7x+6=0后等式成立,所以1是方程、x3-7x+6=0的解,类似的2,-3也是方程的解.
(3)进一步归纳方程求解的一般方法,给出一元三次方程的公式解法:肯定赋值法和公式解法对方程求解的通用性与一致性.通过说明用赋值法求解一元三次方程的不便,提供一元三次方程的公式解.引导学生用一元三次方程的公式解进一步求解、x3-7x+6=0.
背景介绍:早在公元前4-5世纪数学家们很早就已经发现了一次方程和二次方程的一般解法,而三次方程的公式解直到16世纪才由数学家卡丹给出.对方程x3+px+q=0,它的公式解为
学情预设生:

(4)探究发现、出现障碍:求解方程有两种方法:赋值法、公式解法;在一次和二次方程的求解中,两种方法得到的解之间保持着一致性.但是,运用两种解法求解三次方程x3-7x+6=0得出的结果却出现了不一致.故引导学生探寻造成这种结果的原因.
设计意图在学生尚未形成复数的概念时,通过求解具体方程,并抽象归纳出相应方程及求解方程的一般方法,使学生发现求解三次方程的两种方法之间的不一致,从而使学生产生认知冲突并产生探究欲望.
(三)深入思考
(1)学生探究,提出猜测:
问题2:猜测造成使用两种方法求解一元三次方程x3-7x+6=0得到的结果不一致的原因是什么?
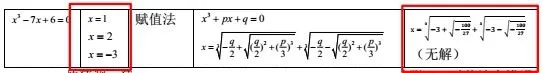
提出可能的猜测,猜测一:人为错误,如运算、公式抄写错误;猜测二:赋值法有错误;猜测三:公式解有错误.并对这些猜测进行分析、排除;经过反复检查,没有出现代入、抄写错误,排除猜测一;由于“赋值法”是求解方程的原始方法,排除猜测二;三次方程的公式解已为人们所证实,排除猜测三.
(2)深入思考,提出猜想:
问题3:用公式解求解方程x3-7x+6=0后,使得方程x3-7x+6=0从有解到无解,发生了质的转变,对此你有何感想?
引导学生从“方程x3-7x+6=0使用了公式解法后,方程x3-7x+6=0从有解到无解发生了质的转变”出发,考虑造成这种结果的原因是用公式法时,基于负数开平方在实数集中无意义,于是得到方程无解的结论.从而提出猜想:负数可以开平方,有意义.
背景介绍:给出三次方程公式解的数学家卡丹,他在求解三次方程时也遇到了类似问题.但是卡丹并没有因为这个猜测不合乎情理而置之不理,他坚持继续运算,最终算出了结果这与我们用赋值法得到的解的结果一致.
设计意图对用两种方法得到方程x3-7x+6=0的两个不一致的解的原因进行探讨,从而导出问题:负数是否可以可平方?
(3)寻求猜想的合理性:负数可以开平方,负数开平方后所得的这类数存在于实数之外!
问题4:负数可以开平方吗?负数开平方后真的有意义吗?
引导学生回顾开平方运算,从开平方运算的概念:若∀m∈R,有m2=n,则n≥ 0,记进行思考得到:在过去的学习中,负数不可以开平方是因为实数的平方都是非负数.进而尝试考察上述命题的逆否命题:若n<0,则∃m∈/R,有m2=n,于是发现猜想的合理性.提出结论:负数应该也可以开平方,只是它并不属于实数集,它存在于实数集之外!因此,得到有意义,它的意义也在实数集之外.
因此,这促使我们为了求解方程需要对实数集进行数系扩充.继而引导学生列举一些例子以使学生感受到猜想的合理性:确实存在着许多实数集之外的数.如
设计意图分析负数开方的条件,从而使学生理清思路、解决认知冲突,并理解引入新数的必要性.培养演绎推理能力和探究精神.
(四)形成概念
(1)形成虚数单位与纯虚数的概念:

称形如bi(b∈R,b/=0)的数为纯虚数,所有纯虚数的全体称为纯虚数集.
设计意图通过再列举形如的例子形成纯虚数的概念,并提出引入虚数单位i来表示以及用bi(b∈R,b/=0)来简化表示纯虚数.
(2)进一步寻找其它属于实数集之外的数:
问题5:那么除了纯虚数以外,还有其它不属于实数集,而属于实数集以外的数吗?
引导学生仍然从方程入手.此前,从方程求解入手,发现了在实数集以外存在着大量的数;那么观察他们使方程的解产生了怎样的变化?在上述的一次、二次、三次方程中,大量的方程都是有实数解的,而不涉及属于实数集以外的数.可以考虑,二次方程无实数解的情况(∆<0).
问题6:请结合新学的纯虚数的概念求解方程x2+x+1=0.
学情预设生:方程x2+x+1=0的解为
引导学生从上述的方程求解中发现,由于∆=-3<0,方程无实数解;于是并不属于实数集;但是从结构上看,也并不是纯虚数,它由实数和纯虚数用加减符号连接共同组成.由此可见,不属于实数集的数还有另外一种类型!
(3)形成非纯虚数的概念:
称形如a+bi(a,b∈R,a,b/=0)的数为非纯虚数,如,所有非纯虚数的全体称为非纯虚数集.
(4)形成虚数、复数的概念,对新学的数以及已学的数进行归类:
把纯虚数和非纯虚数统称为虚数,其形式为a+bi(a,b∈R,b/=0);所有虚数全体构成的集合为虚数集.把虚数和实数统称为复数(complex number),其形式为a+bi(a,b∈R);同时复数常用字母z表示,即有z=a+bi(a,b∈R),这种表示我们称为复数的代数表示,其中a,b分别为复数的实部和虚部;称所有复数的全体构成的集合为复数集,记为C.
于是,可以得到如下的图示:

(5)得出结论:除了实数还有其它数,这就是虚数;存在比实数集范围更大的数集,这就是复数集.
设计意图继续结合方程进行探究,进一步形成非纯虚数、复数的概念以及得到复数的代数形式、复数集与其它数集的关系,使学生更深刻的体会方程与数的联系.
(五)巩固运用
根据复数的代数形式与纯虚数等概念的关系,求解下列问题:
(1)实数m取什么值时,复数z=m+1+(m-1)i是:(i)实数;(ii)虚数;(iii)纯虚数.
(2)指出下列各数中,哪些是实数,哪些是虚数,哪些是纯虚数.为什么?
学情预设(1)(i)实数,于是m-1=0,即m=1;(ii)虚数,于是m-1/=0,即m/=1;(iii)纯虚数,于是m+1=0且m-1/=0,即m=-1.

设计意图根据桑代克的练习律与斯金纳的强化原理,使学生掌握复数的代数形式与纯虚数、实数等的联系.
(六)小结与作业
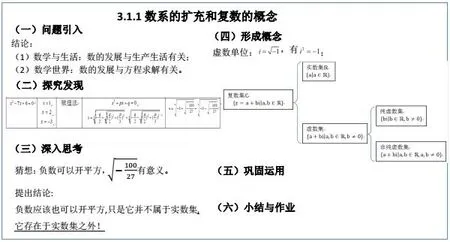
(1)课堂小结:与学生共同总结梳理本节课的复数概念形成思路:
1、从数学史和已学知识出发,回顾数的发展过程.
结论:(1)数学与生活:数的发展与生产生活有关;(2)数学世界:数的发展与方程求解有关.
于是,促使从方程求解出发思考数的进一步发展.
2、在求解方程的过程中,归纳得到方程求解的两种方法:“赋值法”和“公式解”.其中在这两种方法下,三次方程x3-7x+6=0得到的解不一致,进而发现实数集之外的数,而且这个数的平方为负数;同时,意识到实数集已经不够用了!
3、引入新的实数集之外的数的概念:虚数单位、纯虚数、非纯虚数、虚数;以及相应的数集的概念:纯虚数集、非纯虚数集、虚数集、复数集.此外,还得到了复数的代数表示以及复数集与其它数集的关系.
纯虚数:bi(b∈R,b/=0);
非纯虚数:a+bi(a,b∈R,a,b/=0);
虚数:a+bi(a,b∈R,b/=0);
复数(代数表示):z=a+bi∈C(a,b∈R).

设计意图归纳本节所学内容,回顾探索思路历程,强化数学系扩充的思想.
(2)作业:
必做:①课本练习题P104第1题、P106第2、3题;
思考:①复数是否具有几何意义?它的几何意义是什么?结合书本3.1.2.②复数集是否满足运算规律(加法结合律、加法交换律、乘法结合律、乘法交换律、乘法对加法的分配律)?
设计意图练习强化复数的概念以及相关知识.
板书设计
附:
本教学设计的创新之处
①从方程x2+1=0有解入手来引入复数概念是不符合历史事实的,而且难以让人接受.根据HPM的教学理念,遵从复数概念发展的历史原貌来设计教学.
②由灌输概念式教学转向揭示数系扩充过程的教学,体现了数学新课程所倡导的过程教学理念.
③借用数系发展的历史情境和方程求解为线索,问题驱动,环环紧扣,层层深入,让学生经历了方程求解探索的一般过程,学到的不仅仅是言语连锁水平的复数概念,而是学到了理解复数概念引入的必要性与合理性,以及数系扩充的思想,化解了复数概念理解的难点.
[1]何小亚,姚静.中学数学教学设计[M].北京:科学出版社,2012.
[2]何小亚.数学学与教的心理学[M].广州:华南理工大学出版社,2011.
[3]李忠.复数的故事[M].北京:科学出版社,2011.

