巧用“变式教学”解高中数学疑惑

蔡汶剑

（漳州市第三中学，福建 漳州 363000）

章建跃在《数学教育心理学》中提到：变式就是变更对象的非本质特征的表现形式，变更观察事物的角度或方法，以突出事物的本质特征，突出那些隐蔽的本质特征。这就要求教师在教学过程中，善于改造题目，充分利用一题多解，让学生从不同的角度出发，对题目本身进行相应地理解以及挖掘。另一方面，也要求教师在教学过程中，循序渐进地对题目进行不断地变式，由浅入深，让学生充分讨论以及探究，以便更好地答疑解惑。

一、变式教学的作用

所谓“变式教学”，是指教师从教学目标出发，设计一系列层层相扣的问题，由易到难，层层递进，不断地改变思考的角度，让学生可以充分独立思考，思维得到发散的一种教学方法。从2016年福建高考使用全国卷以来，数学文理科的难度和梯度都有所提升，很多题目必须深入理解才能真正得到答案，这就要求教师在教学过程中，加强题目的变式训练，针对一题多解和一题多变，利用变式技巧将题目简便化以及直观化。巧用变式，让学生对知识体系结构更加地清楚明了，也有助于学生自主探究能力的提升。

二、不同教学过程中的变式设计

变式教学中，教师要遵循针对性原则。所谓针对性原则是指从教学对象的实际认知发展水平出发，对于新授课、习题课、复习课列举不同的变式题型以及方法。新授课的变式主要以完成教学目标为主，变式主要从教学目标出发；习题课的变式可以适当增加数学思想和方法；复习课的变式除了习题课的元素，还要注意发散思维，让学生找出题目与题目之间的联系与区别。另外，变式更要从教学对象出发，例如在高二文理分科之后，文科教学中，变式的难度和深度要明显浅显于理科，对于文科的学生，不宜一下子难度增加过大，对于一题多解的题目，可以结合代数法和几何法从旁佐证再进行变式。

新授课是一种传授新内容、讲解新知识的授课。其在教学过程中，所占比重最大，学生主要通过新授课的教学，掌握新知识，联系旧知识。学生对于新知识的掌握程度好坏主要取决于新授课，这就要求教师指导学生如何衔接新旧知识。下面以选修4-4的《极坐标系与参数方程》为例，例举一题进行变式。

此题意在让学生掌握极坐标系、参数方程、直角坐标方程之间的互化，作为新授课，此题的题干以及求解的两个问题很好地体现了互化的问题，并且此题还跟以前所学习过的解析几何进行了衔接，让学生利用数形结合进行求解。在此基础上，教师可以将再进一步进行变式。

例2：在直角坐标系XOY中，直线L的参数方程为（t为参数）在极坐标系（与直角坐标系XOY取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为P＝4cosθ

（1）求圆C在直角坐标系中的方程；（2）若圆C与直线L相切，求实数a的值

习题课是通过对题目的讲解实现学习效果的评价,以学生作业和练习为主要目的的授课。在习题课中，通过对习题的理解和练习，巩固新知识，拓展新问题，展开剖析，让学生结合教材知识点，提取相关的信息，迁移知识，构建体系，强化方法和规律技巧。让学生学会思考、学会分析，举一反三。所以，习题课的课时虽然不多，但在课堂教学中起着举足轻重的作用。

此题是求三角函数最值的问题，教师在学生掌握三角函数化一公式的基础上进行讲解，并通过数形结合让学生直观上看出函数的最大值以及最小值。在此基础上，可再加入二倍角公式的应用，以及换元的思想，逐步加深，让学生在充分理解三角函数公式的基础上，强化数形结合的思想。

复习课是以总结知识规律，总结答题规范和方法技巧，总结学习方法，进行反思的授课。所以复习不是简单的重复，需要在原有的基础上进行总结，挖掘教材、拓展教材以加深理解。

三、不同教学对象的变式设计

下面以立体几何——2017年全国卷I第17题为例，提出教师针对不同教学对象如何设置不同的变式设计：

在高中阶段，立体几何是必修二的内容，教学对象为所有的高中生。立体几何是历年高考的重要考点，学生在初中只接触过平面几何的内容，对于立体几何的内容是完全陌生的。但到了高中阶段，学生的思维能力得到迅速发展，空间想象能力和抽象逻辑思维也得到很大的提高。在必修二的内容中，立体几何适用于所有的学生，但到了高二文理分科之后，理科在必修二的基础之上，多了空间直角坐标系的内容，于是理科生有更多的方法来解答立体几何，并且相对于文科生，理科生的空间想象能力略高于文科生，因此在本题的设置中要抓住文理科的共同点和不同点进行相应的变式。

高考中，立体几何的线线垂直、线面垂直、面面垂直的性质定理是重点也是难点。并且此内容是必修二的内容，在文理分科之前学生都应掌握理解，因此，在此题第一问的设计上，可从文理科的公共点出发设置疑问，如下：

例6：如图，在四棱锥P-ABCD中，AB//CD，且∠BAP=∠CDP=90°

证明：平面PAB⊥平面PAD

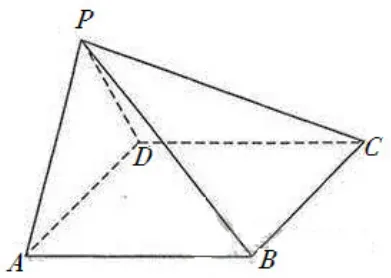
在第二问的设置上，可从学生的接受程度进行变式，文科的题目可从表面积、体积、高等问题提出疑问，理科的题目可在文科的基础上，再增加线面所成的角、二面角的夹角大小问题进行变式。因此，第二问的设置上，文科可变式为：

而对于理科，可将第二问变式为：

（2）若PA=PD=AB=DC，∠APD=90°，求二面角A-PB-C的余弦值。

此题目的设置主要是针对文理科学生学习的接受程度，知识的掌握程度不同，而将题目的问题进行变式。对于文科而言，如何利用体积转化为底面积、高、侧面积等是学生需要掌握的重点，同时也是一大难点。很多学生立体感比较强，可以借助高来求解，而对于立体感较弱的学生，则可通过等体积法得到求解。对于理科而言，在选修中多了空间坐标系，于是，更多的学生会选择建系的方法，从而把看似复杂的问题简单化。教师在教学过程中，要针对近几年全国卷的特点，分析文理差异，在此类型中多做变型和拓展，也可将锥变式为球或者柱再让学生加以练习。

在教学过程中，教师要从教学目标出发，研究教学对象，提出合适的变式教学的内容。在变式教学过程中，如何把握变式教学的数量、质量、梯度是教师今后应该加强和提高的地方。巧用变式教学，让学生主动参与教学过程中，体现其主体地位，可激发学习热情，更可以提高学生的素质能力，起到答疑解惑的作用。

［1］孟令奇,张德利.跨文化视角下的中国数学教育特点探析——到底什么是中国式的数学教学［J］.数学教育学报，2013（12）.

［2］肖凌戆.数学教育要以理性思维育人——我的数学教学主张［J］.中国数学教育，2016（5）.

［3］刘勤，何长林.去其浮华，挖掘数学教育的本质——一堂高三“等差数列复习课”的教学实录与改进［J］.数学教学通讯，2015（12）.