奇异分数阶Laplacian方程正弱解的存在性及正则性

王兴

(西安理工大学理学院,陕西 西安 710054)

1 引言

随着现代科技的发展,经典的Laplacian算子在描述物理、化学、生物甚至是金融学中的新现象和新的客观规律时具有很大的局限性.上个世纪八十年代以来,随着相变理论、反常扩散、黏弹性力学、材料力学、多孔介质力学、多重散射、量子力学、信号和系统识别[1-4]等领域的发展,研究人员发现分数阶Laplacian方程相较于整数阶微分方程能更好地描述涉及记忆、遗传效应以及路径依赖和全局相关性的物理过程.因此,近些年来,分数阶微分方程理论及应用方面的研究得到了许多学者的广泛关注并有着迅猛发展.

本文讨论一类来源于非牛顿流体、弹性电介质膜和微型机电系统中的含奇异项的分数阶Laplacian方程:

其中Ω是N维空间RN中的有界光滑区域,是非负函数,λ＞0是实参数.由于所以,称此类方程为奇异方程.

自上世纪60,70年代以来,含有奇异项的经典Laplacian方程:

得到了广泛关注.1977年,文献 [5]利用逼近方法得到,当λ=0,p(x)∈Cα(Ω)时,奇异Laplacian方程(Q)有唯一的古典解,成为该领域奠基性工作.2001年龙以明院士等[6]利用Ekeland变分原理,研究了次临界增长下奇异Laplacian方程:

证明了当λ较小时,方程有2个正弱解.2013和2014年,文献[7-8]将上述工作推广到临界情形得到了当λ较小时,上述方程正弱解和古典解的存在性.2017年,文献[9]又得到了超临界增长时,上述方程正弱解的存在性与正则性.目前,针对奇异分数阶Laplacian方程的研究更为少见.已有的主要工作是,2014年,文献[10]考虑了如下奇异分数阶问题:

其中0＜s＜1,γ＞0.利用扰动方法,作者得到了该问题正弱解的存在唯一性.文献[11]运用构造逼近解序列的方法,得到了如下具有临界增长指数的奇异分数阶Laplacian方程在特定弱意义下解的存在性和多重性,

其中

本文将在已有工作的基础上,首次运用闭锥上的临界点理论,研究非线性项具有任意增长性的奇异分数阶Laplacian方程.此方法,为研究奇异分数阶方程提供了新的有效途径.

2 预备知识[12]

定义 2.1设Ω⊂RN是光滑有界区域,p≥1,s∈(0,1),则分数阶Sobolev空间定义为

并赋予范数

特别地,当p=2时,记Hs(Ω)=Ws,2(Ω),且Hs(Ω)依内积

构成Hilbert空间.

定义 2.2设Ω⊂RN是光滑有界区域,p≥1,s∈(0,1),则分数阶Sobolev空间定义为按照范数的完备化空间.特别地,当p=2时,记

定义 2.3设s∈(0,1),定义分数阶Laplacian算子(−∆)s为:

引理 2.4(嵌入定理)设 Ω⊂RN是光滑有界区域,s∈(0,1),N＞2s,则存在常数C∗=C(N,s,Ω),使得不等式

成立,其中

定义 2.5若,使得等式

成立,则称u是问题(P)的弱解.

引理 2.6设λi是Laplacian方程

的特征值,φi是相应的特征函数,s∈(0,1),N ＞2s,则是分数阶Laplacian方程的特征值,φi是属于λsi的特征函数.

根据椭圆方程理论知,引理2.6中的特征函数列φi是L2(Ω)空间的一组完备正交基,所以可定义如下空间.

定义 2.7设函数u∈L2(Ω),若存在序列{µi}满足

使得

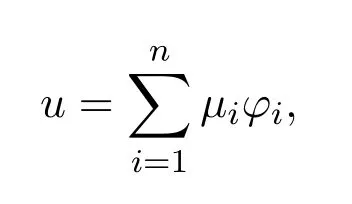
则称u属于空间H,即

并赋予范数为

由文献[13]知,空间H在范数‖·‖H下构成Banach空间,且H ⊂H−s(Ω).

3 主要结果

定理 3.1设Ω⊂RN(N≥3)是有界光滑区域,

f(t)是局部Lipschitz函数,满足下列条件f(0)=0,f(t)＞0,以及

则存在Λ＞0使得当λ∈(0,Λ)时,方程(P)至少有一个正弱解

其中λ1,φ1分别是Laplacian方程的最小特征值及其特征函数.

注 3.1由于分数阶Laplacian方程(P)具有奇异非线性项p(x)u−γ,所以方程(P)相应的能量泛函

在全空间不是Frechet可微的.因此不能直接运用临界点理论寻求方程的弱解,这给问题的研究带来本质上的困难.经过计算发现,当能量泛函限制在正则函数构成的闭锥上是Frechet可微的.所以,针对奇异分数阶Laplacian方程我们首次运用闭锥上的临界点理论证明定理3.1.

4 定理3.1的证明

令

显然E是分数阶Sobolev空间的稠密子集,且对于任意的ε＞0集合是E的闭锥.下面给出能量泛函在闭锥上的Frechet可微性.

引理 4.1能量泛函Jλ(u)在上Frechet可微,且在弱意义下Jλ(u)的Frechet导数为:

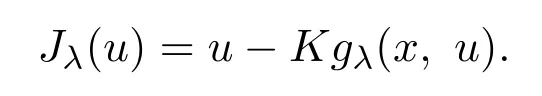
证明首先令

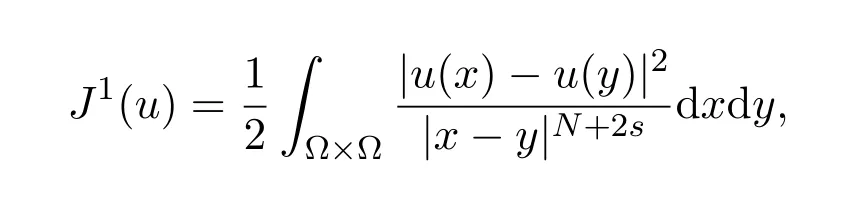
则

因此

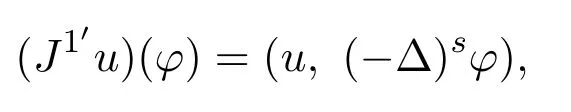
即在弱意义下有J1′u=u成立.

其次,令

下证J2(u)在闭凸集上Frechet可微.对于任意取定的以及任意ν ∈E,当t充分小时由积分中值定理得

其中θ(x)∈[0,1]是Ω上的可测函数.注意到由u≥εφ1,可得

意义的.进一步计算得

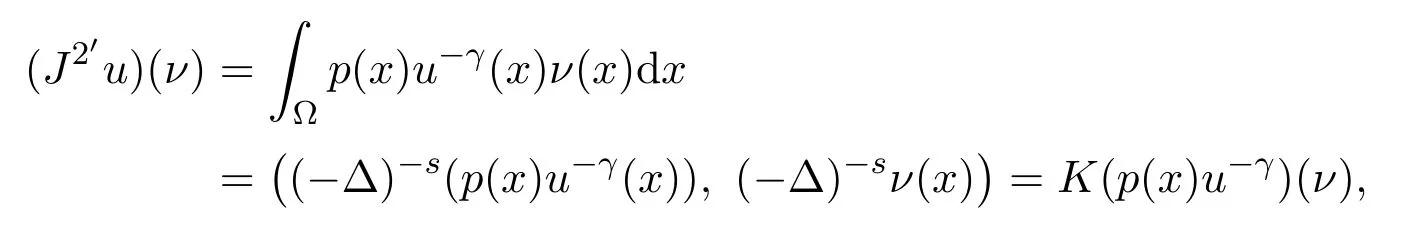
即在弱意义下有J2′(u)=K(p(x)u−γ).

最后令

利用f的局部Lipchitz连续性,令t→0,得

因此,在弱意义下有J3′u=K(f).综合上述讨论可得Jλ(u)在 Πε上Frechet可微,且引理4.1得证.

引理 4.2对于任意取定的λ＞0,若是方程 (P)的正弱解,则存在实数ε(λ)＞0 使得u ∈Πε(λ).

证明由定理3.1的 (F1)得:存在常数M1＞0,δ1＞0,使得当

时,有

再由定理3.1的(F2)得:存在常数M2＞0,δ2＞0使得,当

时有

因此,由定义 2.7,存在h(x)∈H−s(Ω),使得

即在弱意义下有

由文献 [13]中引理2.4和引理2.5得:存在紧子集ω⊂⊂Ω,有ηω=essinf|ωu＞0;且存在常数Cω＞0使得u(x)＞ Cωd(x),∀x∈Ωω,其中d(x)=d(x,∂Ω)是点x到边界∂Ω 的距离.从而,再利用φ1的整体正则性得:存在常数ε(λ)＞0,使得u(x)≥ ε(λ)φ1(x),∀x∈Ω.

进一步,得

由文献[14]中的定理1.5得:正弱解

因此,存在实数ε(λ)＞0 使得u ∈Πε(λ).

引理4.2得证.

引理 4.3存在 Λ＞0,使得当λ∈(0,Λ),条件(F1)与(F2)成立时,能量泛函Jλ(u)在闭锥 Πε(λ)上满足 PS 条件.

证明设{un}⊂Πε(λ)是Jλ(u)对应的PS序列,即|Jλ(un)|≤C,且下证{un}有子列在Πε(λ)中收敛.因为所以对任意的有

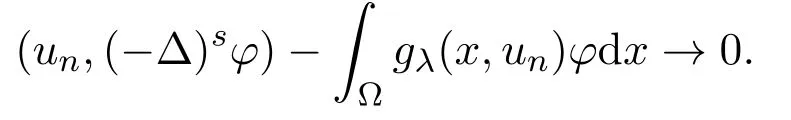
特别地,取φ=un,得

因此可得

另一方面,由(1)式和Hölder不等式知,存在C′＞0使得

由条件(F1)与(F2)得:存在常数C′＞0使得

由引理2.4的(1)式,上式(4)可进一步放缩为:

将(3),(5)式代入(2)式得

显然存在充分小的 Λ＞0,使得当λ∈(0,Λ)时,有 1−λC′C∗＞0.从而由 (6)式得有界,即{un}是中的有界集.

另一方面,由引理4.1得:

因此

其中 (7)式左边的K=(−∆)−s是紧算子.借助于{un}的有界性,得到o(1)+Kgλ(x,un)是中的列紧集.因此 (7)式右端的{un}是中的列紧集,所以有子列在中强收敛于

因此,u ≥ ε(λ)φ1,且运用引理4.2同样的证明方法,得到综上得u ∈Πε(λ),所以Jλ(u)在闭锥 Πε(λ)上满足 PS 条件.

引理4.3得证.

定理 3.1的证明由于Jλ(u)在闭锥Πε(λ)上满足PS条件,由变分学知识,我们只需证明能量泛函Jλ(u)是强制的.从而Jλ(u)在Πε(λ)上存在临界点,即为方程(P)的正弱解.

由(3)式,存在常数C1＞0使得对于任意的u∈Hs0(Ω),有

由条件(F1)得:存在常数N1＞0,ε1＞0,使得当x∈Ω1={∈Ω|0≤u(x)＜N1}时,有

由条件(F2)得:存在常数N2＞N1,ε2＞0,使得当x∈Ω2={∈Ω|u(x)＞N2}时,有

显然,当x∈Ω(Ω1∪Ω2)时有N1≤u(x)＜N2.因此,存在常数C2＞0,使得

从而

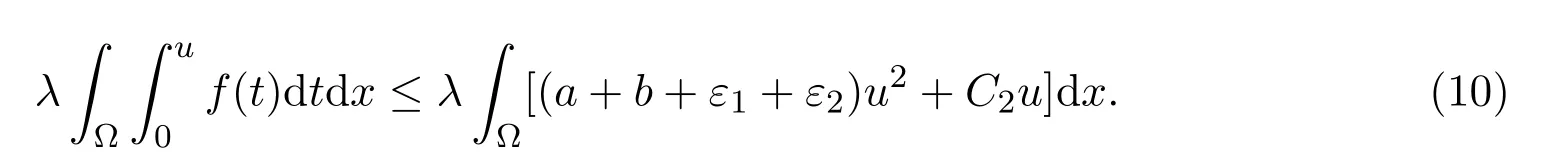
因此,由 (8),(10)以及 (1)得:对于任意的u∈Πε(λ),有

所以,Jλ(u)在闭锥Πε(λ)上是强制的下方有界的.

定理3.1得证.

[1]Caffarelli L.Further regularity for the Signorini problem[J].Comm.Partial Differential Equations,1979,4:1067-1075.

[2]Caffarelli L,Vasseur A.Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation[J].Annals of Mathematics.Second Series,2010,171:1903-1930.

[3]Craig W,Groves M.Hamiltonian long-wave approximations to the water-wave problem[J].Wave Motion,1994,19:367-389.

[4]Craig W,Schanz U,Sulem C.The modulational regime of three-dimensional water waves and the Davey-Stewartson system[J].Ann.Inst.H.Poincare,Anal.Non-Lineaire,1997,14:615-667.

[5]Crandall M G,Rabinowitz P H,Tartar L.On a Dirichlet problem with a singular nonlinearity[J].Comm.Partial Differential Equations,1997,2:193-222.

[6]Sun Y J,Wu S P,Long Y M.Combined effects of singular and superlinear nonlinearities in some singular boundary value problems[J].J.Differential Equations,2001,176:511-531.

[7]Wang X,Zhao L,Zhao P H.Combined effects of singular and critical nonlinearities in elliptic problems[J].Nonlinear Anal.,2013,87:1-10.

[8]Wang X,Zhao P H,Zhang L.The existence and multiplicity of classical positive solutions for a singular nonlinear elliptic problem with any growth[J].Nonlinear Anal.,2014,101:37-46.

[9]Wang X,Qin X Q,Hu G.Existence of weak positive solution for a singular elliptic problem with supercritical nonlinearity[J].Anal.Math.Phys.(2017).http://doi.org/10.1007/s13324-016-0162-4.

[10]Fang Y.Existence,uniqueness of positive solution to a fractional Laplacians with singular nonlinearity[J].Mathematic.Preprint(2014),http://arxiv.org/pdf/1403.3149.pdf.

[11]Mukherjee T,Sreenadh K.Critical growth fractional elliptic problem with singular Nonlinearities[J].Preprint(2017),http://arxiv.org/pdf/1602.07886.pdf.

[12]Giovanni M B,Vicentiu D R,Raffaella S.Variational Methods for Nonlocal Fractional Problems[M].Cambridge:Cambridge University Press,2016.

[13]Capella A,Davila J,Dupaigne L,et al.Regularity of radial extremal solutions for some non-local semilinear equations[J].Comm.Partial Differential Equations,2011,36(8):1384-1353.

[14]Caffarelli L,RaulStinga P.Fractional elliptic equations,Caccioppoli estimates and regularity[J].Ann.Inst.H.PoincaréAnal.Non-Linéaire,2016,33:767-807.