Euler-Voigt方程组的全局适定性

臧爱彬

(宜春学院应用数学研究中心,江西 宜春 336000)

1 引言

Euler-Voigt方程组由Euler方程组正则化过程得到如下形式:

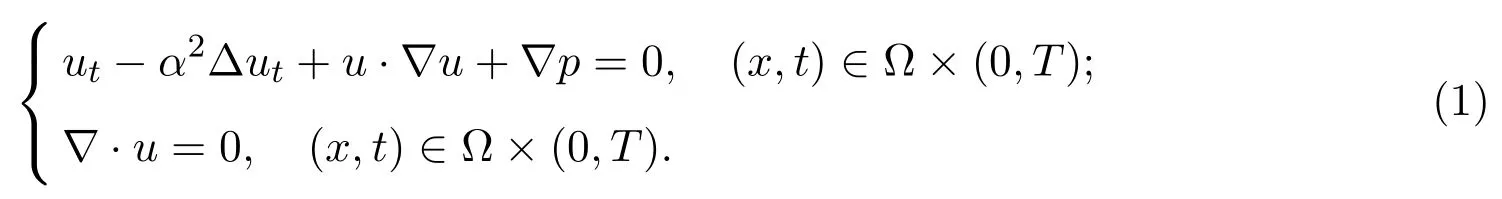
其中T＞0,Ω是Rn(n=2,3)的有界光滑区域,u代表是速度,p为压力,f是外力项以及α为修正参数.

Voigt正则化模型是一类α-修正模型,众多学者[1-8]研究该种模型推导以及应用.Voigt正则化发展型方程也是一类特殊的仿抛物型方程,也就是说具有以下形式的方程:

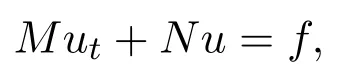
其中,M及N都是非线性甚至是非局部性算子,可参阅文献[9-10]了解更多有关仿抛物型方程的研究.由于Voigt正则的简化性,该α-模型非常适合应用于其他热力学模型,例如文献[11]验证得到二维Q-G方程,还有无粘性Burgers方程的Voigt正则化方程为:

即为著名的水波Berjamin-Bona-Mahony方程[12].文献[13-14]研究有关Voigt正则化的磁流体力学方程和Euler-Voigt方程在周期边界下的全局适定性问题.

本文主要研究方程组(1)初始条件以及具有齐次Dirichlet边界条件,即

的全局适定性问题.

2 记号及预备引理

在陈述以及证明主要结果之前,引进一些常用的记号与引理.记Hs(Ω)是通常的s阶 Lebesgue-Sobolev空间,范数记‖·‖s.特别地,当s=0时,H0(Ω)=L2(Ω),而范数和内积分别记为‖·‖和 (·,·).令

其中n=2,3,为∂Ω的外法向量.是在 Ω中具有紧支集的光滑函数类,是在 Sobolev空间H1(Ω)中的闭包,记

C是与u无关的常数,可能逐行不一样.

现引入具 Dirichlet边界条件下的 Stokes算子,即A=Pσ(−∆),其中Pσ是 Leray-Helmholtz投影算子,记D(A)=(H2(Ω))n∩V.众所周知,空间H具有一组标准正交基{ωj},且该组正交基是A的特征值{λj}对应的特征函数,Aωj=λjωj.另一方面,为克服压力带来的困难,对u,v∈V,令

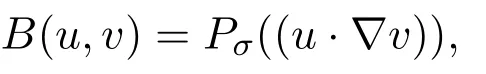
于是B:V×V→V′,进而对于u,v,w∈V易得

为了文章的完整性,引入著名的Aubin-Lions引理如下:

引理 2.1[15](Aubin-Lions引理) 设X0,X和X1都是Banach空间,且X0⊂X⊂X1以及X0紧嵌入X中和X连续嵌入X1中.对于1≤p,q≤∞,记

那么

(i)若p＜∞,则W紧嵌入Lp([0,T];X)中;

(ii)若p=∞以及q＞1,则W紧嵌入C([0,T];X)中.在证明主要结果之前，需要定义初边值问题(1),(2)和(3)的弱解和强解.

定义 2.1设u0∈V,向量函数u∈C([0,T];V)以及满足以下积分等式:

对所有的v∈V成立,则称u是初边值问题(1),(2)和(3)的弱解,进而如果u0∈D(A),则称u是初边值问题(1),(2)和(3)的强解.

3 主要结果及其证明

现陈述并给出初边值问题(1),(2)和(3)的全局弱解存在唯一性定理与证明.

定理 3.1设u0∈V,则存在唯一的向量函数u∈L∞(0,T;V)以及对于任意的T＞0都满足积分等式(5).

证明令其中cj(t)待定.为确定cj(t),则um需满足以下初值问题:

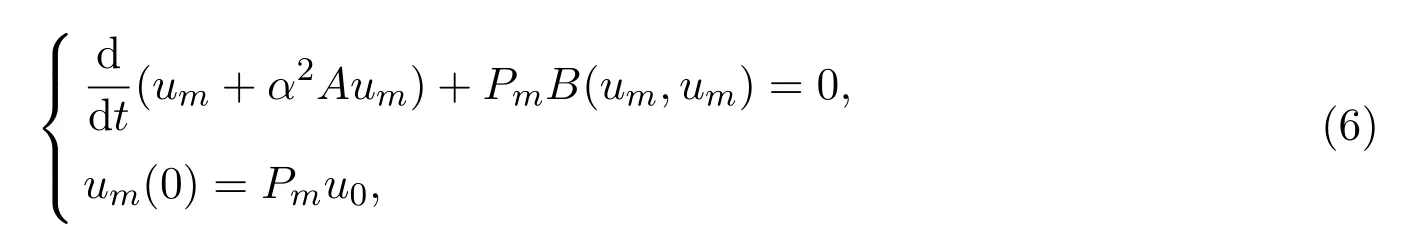
其中Pm是从H到Hm=span{ω1,···,ωm}的正交投影,以及B(um,um)定义如上.

首先,利用算子(I+α2A)−1作用于方程(6),那么方程(6)等价于形如˙y=F(y)的抽象常微分方程组,其中F:Hm→Hm的二次多项式.由常微分方程组存在唯一性定理可知,方程组(6)在区间[0,Tm]存在唯一的一组解um∈C1([0,T];Hm).令是方程组(6)的最大存在区间.

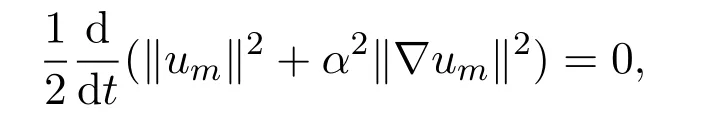
对上式两边在区间[0,t]上进行积分可得

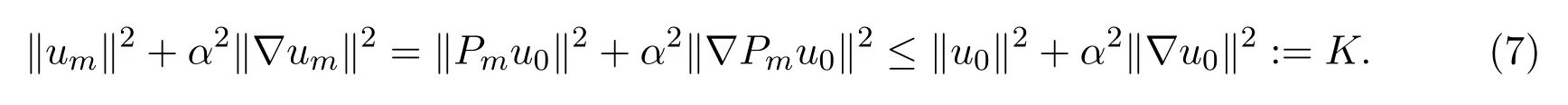
由于上式右端关于m及时间是一致的,于是可推出

另外一方面,利用方程组(6)不难知,

以及

对于任意T＞0,由Banach-Alaoglu定理以及引理2.1,在方程组(6)两边取极限可知,存在一向量函数u以及{um}的一个子列,仍记{um},当m→∞时,

固定k∈N并且m≥k,任取w∈C1([0,T];Hk)且w(T)=0.由(6)易得

首先,由(10),(11)发现当m→∞时,

现只需验证三元线性项的收敛性,即证当m→0时,

为此令

则由(4)可得

因为w∈C1([0,T];Hk)(m≥k),Pmw=w,(7)和(10)以及Hölder不等式易知,I1(m)→0及I2(m)→0,于是I(m)→0.注意到在V中um(0)=Pmu0→ u0.因此在 (14)式中让m→∞以及w∈C1([0,T];Hk)且w(T)=0,有

又因为C1([0,T];Hk)稠于C([0,T];V),从(15)可知u是初边值问题(1),(2)和(3)的弱解.由估计(10)-(13)式以及(I+α2A)−1的有界性知,u∈C([0,T];V)以及

现在证明该解也是唯一的,设u1,u2都是初边值问题(1),(2)和(3)的弱解,将u1,u2代入方程组(1)后相减,令δu=u1−u2得到

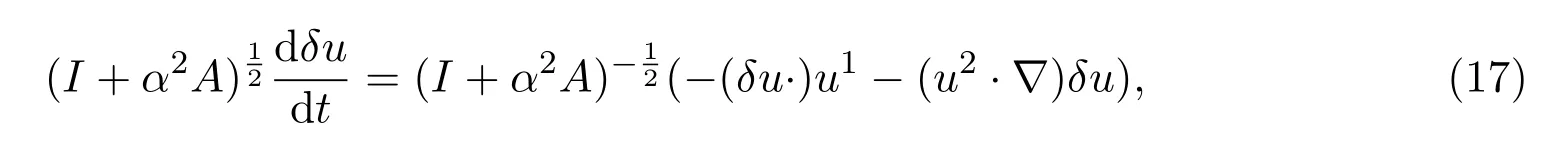
又因为

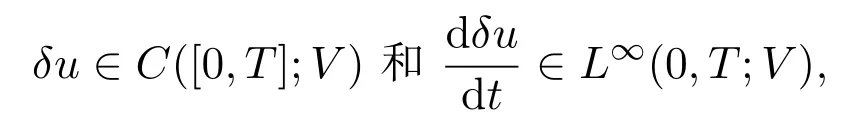
于是

由不等式(18)知唯一性.证毕.

注 3.1在上述定理的证明过程中不等式(18)也蕴含了由定理1.1得到的弱解也是对初值连续依赖的.

利用定理1.1的方法以及类似于Navier-Stokes方程的证明过程[16],可得到以下高阶正则性定理:

定理 3.2设s≥1,u0∈(Hs(Ω))n∩V(n=2,3),则初边值问题(1),(2)和(3)由定理1.1得到的解为u∈L∞([0,T];(Hs(Ω))n∩V).

证明利用算子As(s≥1)的性质以及文献[16]研究有关Navier-Stokes方程的证明过程,具体过程省略.

[1]Cao Y,Lunasin E,Titi E S.Global well-posedness of the three-dimensional viscous and inviscid simplified Bardina turbulence models[J].Commun.Math.Sci.,2006,4(4):823-848.

[2]Chen S,Foias C,Holm D D,et al.Camassa-Holm equations as a closure model for turbulent channel and pipe flow[J].Phys.Rev.Lett.,1998,81(24):5338-5341.

[3]Chen S,Foias C,Holm D D,et al.The Camassa-Holm equations and turbulence[J].Phys.D,1999,133(1-4):49-65.

[4]Chen S,Foias C,Holm D D,et al.A connection between the Camassa-Holm equations and turbulent flows in channels and pipes[J].Phys.Fluids,1999,11(8):2343-2353.

[5]Cheskidov A,Holm D D,Olson E,et al.On a Leray-α model of turbulence[J].Proc.R.Soc.Lond.Ser.A Math.Phys.Eng.Sci.,2005,461:629-649.

[6]Foias C,Holm D D,Titi E S.The three-dimensional viscous Camassa-Holm equations,and their relation to the Navier-Stokes equations and turbulence theory[J].J.Dynam.Differ.Equ.,2002,14(1):1-35.

[7]Holm D D,Titi E S.Computational models of turbulence:The LANS-α model and the role of global analysis[J].SIAM News,2005,38(7):1-5.

[8]Ilyin A A,Lunasin E M,Titi E S.A modified-Leray-α subgrid scale model of turbulence[J].Nonlinearity,2006,19(4):879-897.

[9]Böhm M.On Navier-Stokes and Kelvin-Voigt equations in three dimensions in interpolation spaces[J].Math.Nachr.,1992,155:151-165.

[10]Carroll R W,Showalter R E.Singular and Degenerate Cauchy Problems[M].New York:Harcourt Brace Jovanovich Publishers,1976.

[11]Khouider B,Titi E S.An inviscid regularization for the surface quasi-geostrophic equation[J],Comm.Pure Appl.Math.,2008,61:1331-1346.

[12]Benjamin T B,Bona J L,Mahony J J.Model equations for long waves in nonlinear dispersive systems[J],Philos.Trans.Roy.Soc.London Ser.A,1972,272:47-78.

[13]Larios A,Titi E S.On the higher-order global regularity of the inviscid Voigt-regularization of threedimensional hydrodynamic models[J].Disc.Cont.Dyn.System Ser.B,2010,14(2):603-627.

[14]Larios A,Titi E S.Higher-order global regularity of an inviscid Voigt-Regularization of the three-dimensional inviscid resistive Magnetohydrodynamic equations[J].J.Math.Fluid Mech.,2014,16(1):59-76.

[15]Boyer Franck,Fabrie,Pierre.Mathematical Tools for the Study of the Incompressible Navier-Stokes Equations and Related Models[M].New York:Springer,2013:102-106.

[16]Temam Roger.Navier–Stokes Equations:Theory and Numerical Analysis[M].New York:ACM Chelsea Publishing,1984.