复阶近于凸函数的相邻系数

牛潇萌,李书海

(赤峰学院数学与统计学院,内蒙古 赤峰 024000)

1 引言

设S表示在单位圆盘U={z:|z|＜1}内单叶解析函数

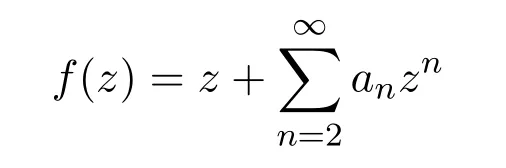
构成的函数类.S∗,C和Bα分别表示通常的星象函数类,近于凸函数类和 Bazileviˇc函数类,它们都是S的子类且S∗⊂C⊂Bα.

定义 1.1[1]设函数f(z)与g(z)在U内解析,如果存在U内Schwarz函数ω(z),满足:

使得

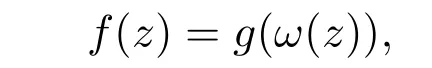
则称f(z)从属于g(z),记作f(z)≺g(z).特别地,如果g(z)在U上是单叶的,则

用P表示在U内解析并且满足条件:

的所有函数

的全体.即P为正实部函数类.

设f(z)∈S,

其级数中相邻两系数模之差||Dn+1(λ)|−|Dn(λ)||的估计是单叶函数论中的一个重要问题.对于f∈S的形式,还尚未完全解决,而且对于相邻两系数模之差的精确估计,在整个族中要办到,是一个很困难的课题.

1946年,Goluzin首先发现了单叶函数相邻系数相互制约的奇特性质,并证明了

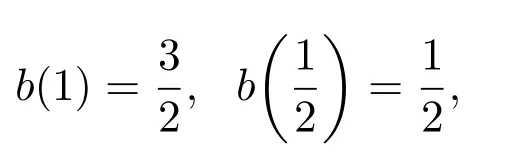
这引起了国内外许多学者的兴趣.近年来许多学者主要研究单叶函数中一些特殊函数族的相邻系数模之差的估计[2-8].

本文研究如下由Al-Amiri和Fernando给出的复阶近于凸函数类C(b)(见文献[9]).

定义 1.2设f(z)∈S,b为复数且b≠0,如果存在g(z)∈S∗,使得

则称f(z)属于复阶近于凸函数类C(b).

Al-Amiri和Fernando在文献[9]中给出了复阶近于凸函数类C(b)的系数估计和偏差定理.Caglar在文献[10]中给出了复阶近于凸函数类C(b)的对数系数,但是其相邻两系数模之差还没有研究.本文研究了复阶近于凸函数的相邻两系数模之差的估计.

2 主要结果

为方便,函数f(z)的幂级数展开式中zn的系数an表示为an={f}n.

引理 2.1[9]设f(z)∈C(b),则对|z|=r＜1和|2b−1|≤1,有

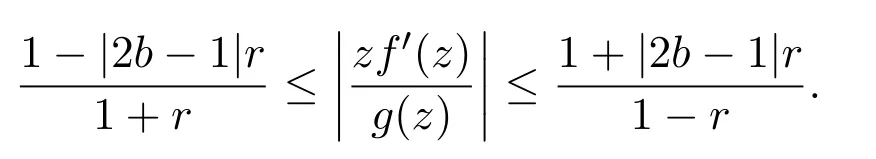
引理 2.2[4]设f(z)∈S,G1(z)=(1−z)f(z)λ−1f′(z)z1−λ,0＜ λ ＜1,则对n≥2有

(1)

(2)

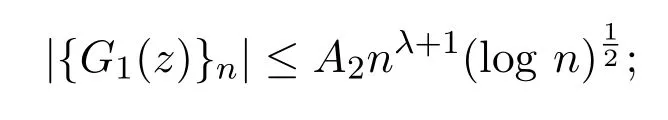
(3)

引理 2.3设f(z)∈C(b),g(z)∈S∗满足:

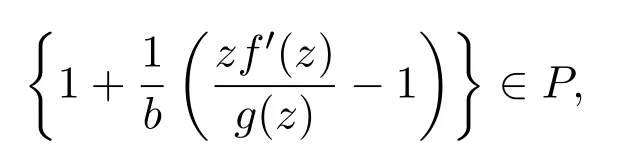
令

则对

有

证明令

则p(z)∈P,由定义 1.1可知,存在解析函数ω(z),|ω(z)|＜1,ω(0)=0,使得

所以

由 Schwarz引理,可知

因此,对z=reiθ,有

由引理2.1,可知

从而

所以

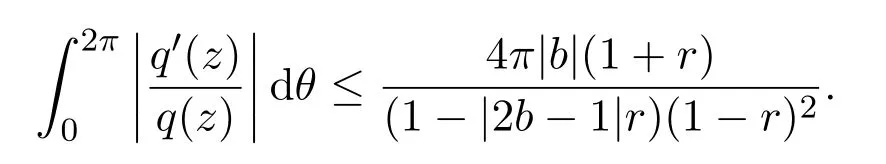
所以对z=reiθ,有

因为当n≥2时有,所以

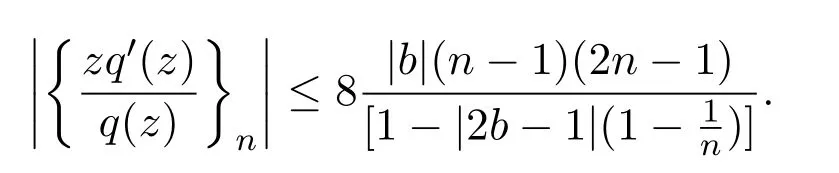
由Schwarz不等式,可知,

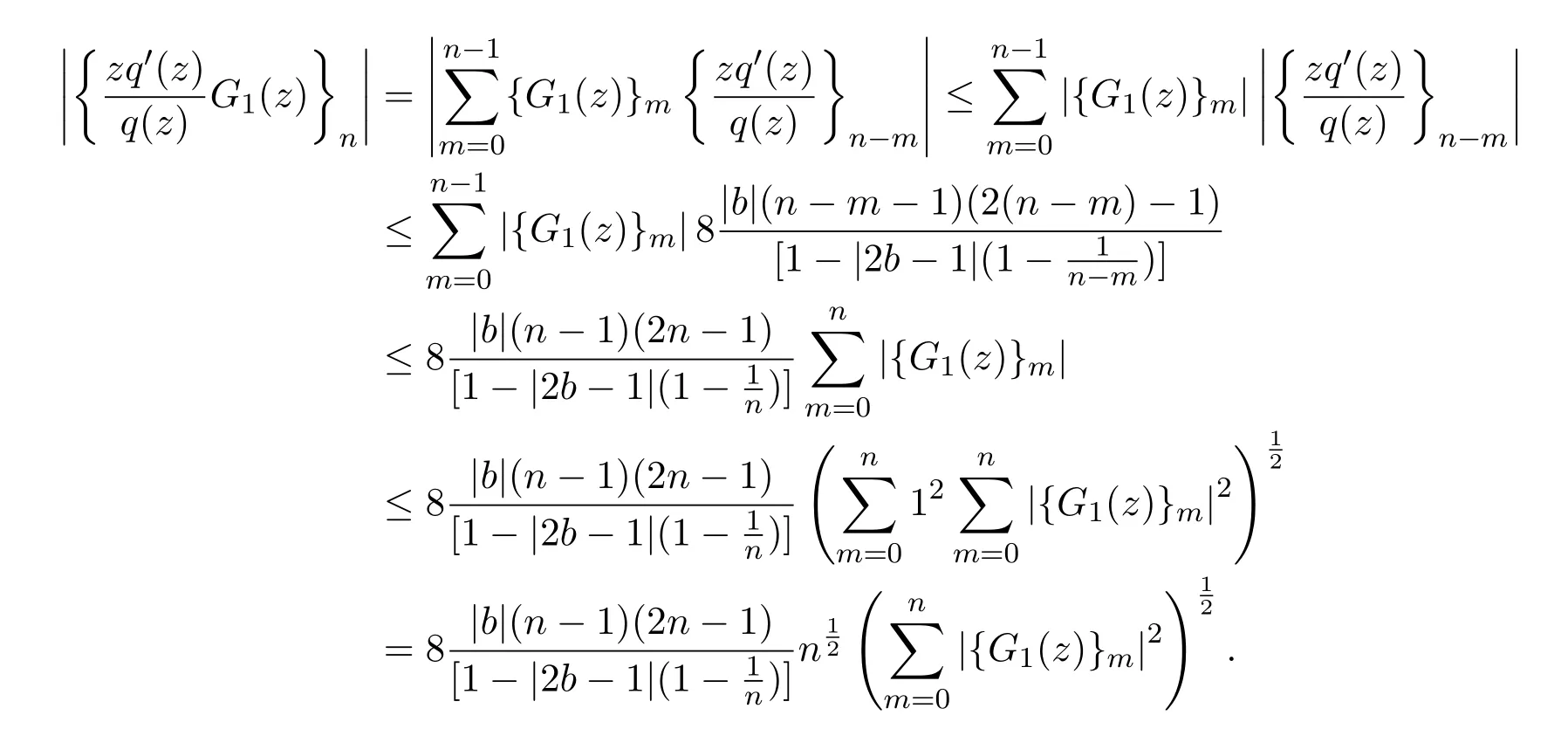
由引理2.2,可知

引理 2.4设f(z)∈ C(b),G1(z)=(1−z)f(z)λ−1f′(z)z1−λ,0＜ λ ＜1,则

证明设f(z)∈C(b),则存在g(z)∈S∗使得

令

易知

从而

所以

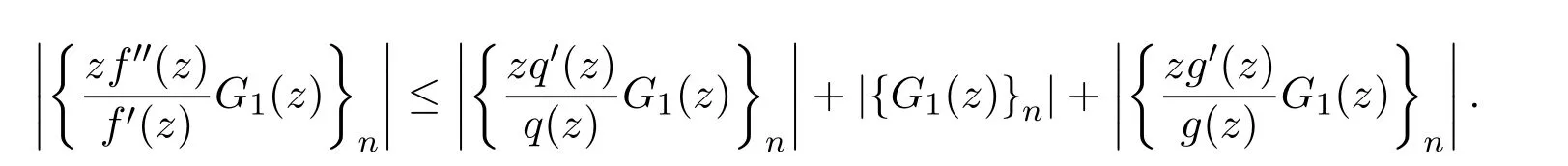
由引理2.2和引理2.3,可知

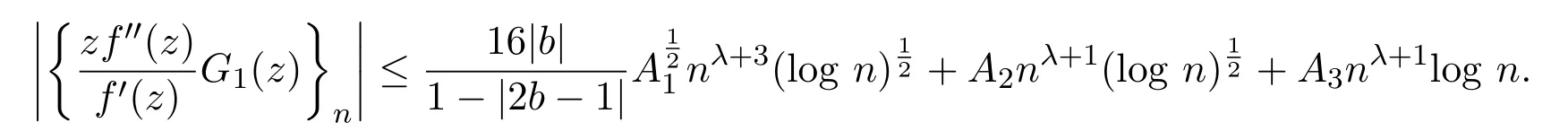
引理 2.5[4]设f(z)∈S,

则

引理 2.6[4]设f(z)∈S,ψ(z)由 (2)式定义,则

定理 2.1设f(z)∈C(b),Dn(λ)由(1)式定义,则对n≥2有

其中

是绝对常数.

证明由(1)式易知

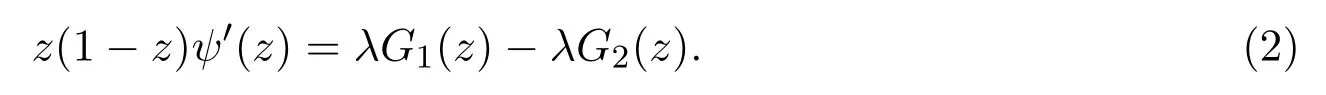
其中

因为

所以

因为

所以由Schwarz不等式可知,

由引理2.2可知

所以由(3)式,引理2.2和引理2.4,可知

即

由引理2.5,可知

由 (2)式(5)式和 (6)式可知

由(1)式,经简单计算可知,

所以

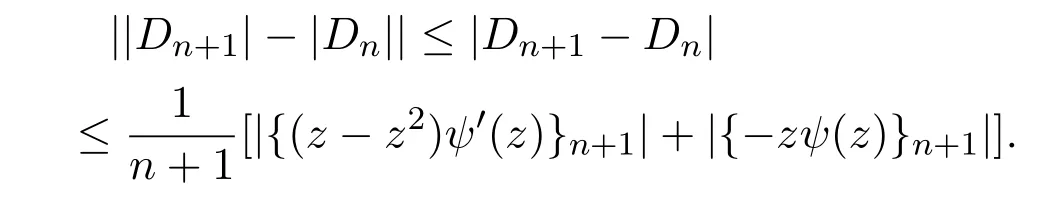
由引理2.6,可知

综上可知,

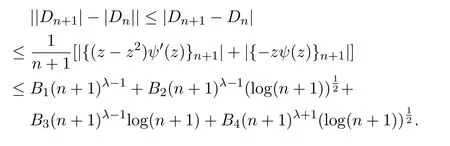
其中

是绝对常数.

[1]Duren P L.Univalent Functions[M].New York:Springer Verlag,1983.

[2]胡克.单叶函数的若干问题[M].武汉:武汉大学出版社,2001.

[3]邓琴,叶中秋.单叶函数相邻两系数模之差的估计[J].江西师范大学学报,2002,26(2):128-131.

[4]邓琴.Bazilevic函数相邻两系数模之差的估计[J].数学学报,2006,49(5):1195-1200.

[5]Leung Y.Successive coefficients of starlike functions[J].Bulletin of the London Mathematical Society,1978,10:193-196.

[6]胡克.论拟凸函数的相邻系数[J].江西师范大学学报,1986,4:1-6.

[7]Ye Zhongqiu.On the successive coefficients of close-to-convex functions[J].Journal of Mathematical Analysis and Applications,2003,283:689-695.

[8]宁菊红,叶中秋.圆对称函数的相邻系数[J].数学研究,2005,38(3):286-291.

[9]Al-Amiri H S,Fernando T S.On close-to-convex functions of complex order[J].International Journal of Mathematics and Mathematical Sciences,1990,13(2):321-330.

[10]Caglar M.The logarithmic coefficient inequality for close-to-convex functions of complex order[J].Journal of Mathematical Inequalities,2015,9(3):951-959.