具反馈控制的一方不能独立生存偏利合作系统的稳定性
杨英钟,王宽程
(闽南理工学院信息管理学院,福建 泉州 362700)
1 引言
近年来,很多学者针对合作生态系统的持久性展开了研究,并得到了相应的研究成果[1-4].而有关偏利合作种群模型的研究工作还很少,祝占法等[5]提出了如下一方不能独立生存的两种群偏利合作模型:
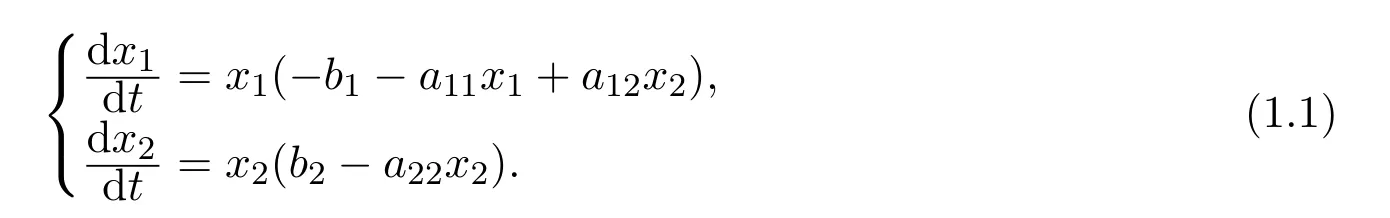
其中bi,aij,i,j=1,2均为正常数,xi,i=1,2是种群在t时刻的生长密度.作者借助向量场分析的方法得出当
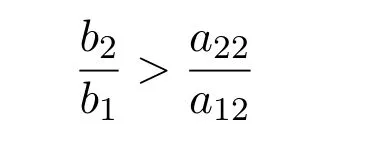
时,系统(1.1)存在唯一全局渐近稳定的正平衡点,并得出种群弱平均持续生存和绝灭的充分性条件.
另一方面,在现实生活中,考虑到生态系统会受到人类的干扰,为此,学者们引入了反馈控制变量.2016年,周晓燕等[6]提出如下具有反馈控制的单方不能独立生存合作模型:
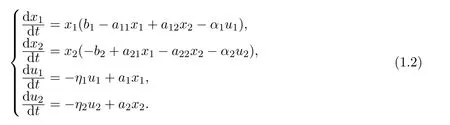
其中ui,i=1,2是反馈控制变量.在文献[6]中,作者通过构造适当的Lyapunov函数,得到研究表明,在原系统存在唯一的全局渐近稳定的正平衡点时,引入适当的反馈控制变量,系统(1.2)仍具有唯一的全局渐近稳定的正平衡点;引入不适当的反馈控制变量,则不能独立生存的第二种群终将绝灭.
注意到至今尚未有学者研究具反馈控制的一方不能独立生存的偏利合作系统:
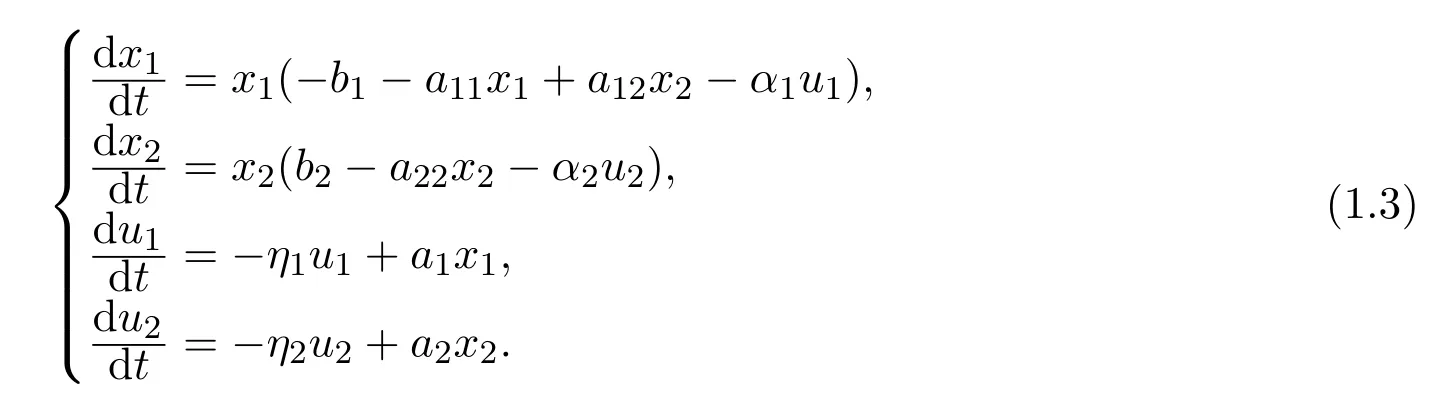
其中,系统(1.3)的所有参数ai,bi,aij,αi,ηi,i,j=1,2均为正常数,xi,i=1,2是种群在t时刻的生长密度,ui,i=1,2是反馈控制变量.其中第二种群对第一种群的生长起有利作用,而第一种群对第二种群的生长不起作用,而且第一种群不能独立生存.本文旨在研究反馈控制变量对系统(1.3)正平衡点和边界平衡点动力学行为的影响.
2 主要结果及其证明
计算易知当条件
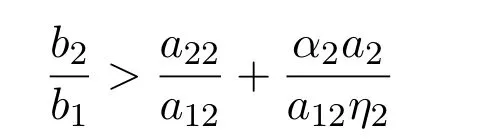
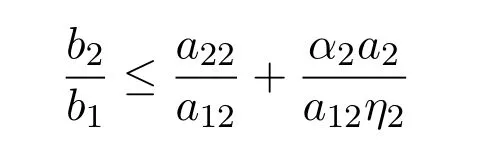
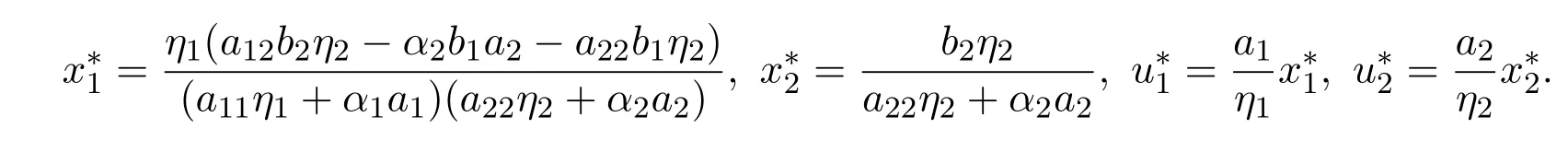
下面探讨系统(1.3)平衡点的稳定性.
定理 2.1若
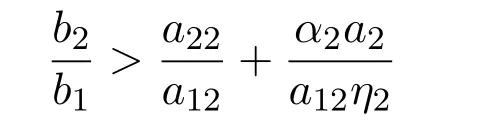
证明注意到满足:
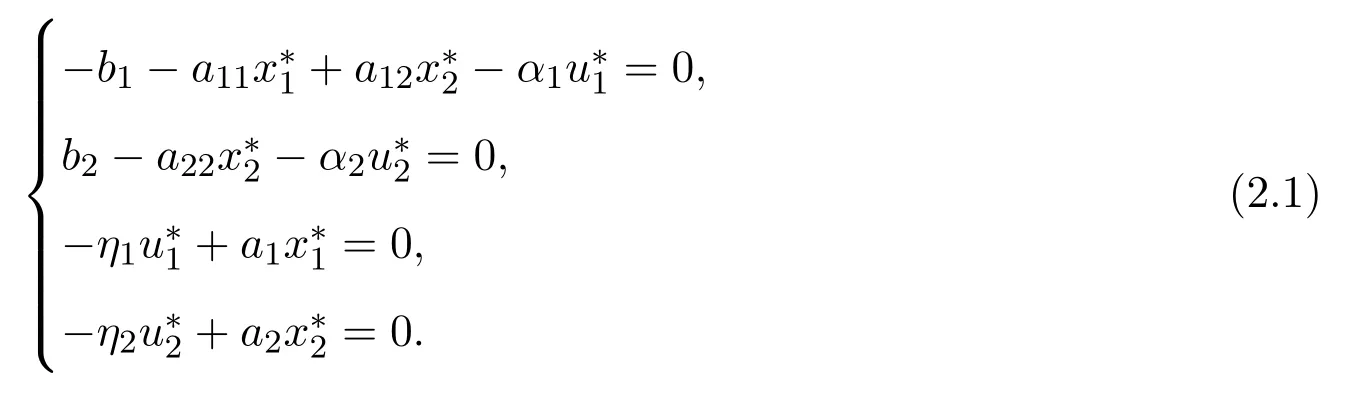
现构造Lyapunov函数:
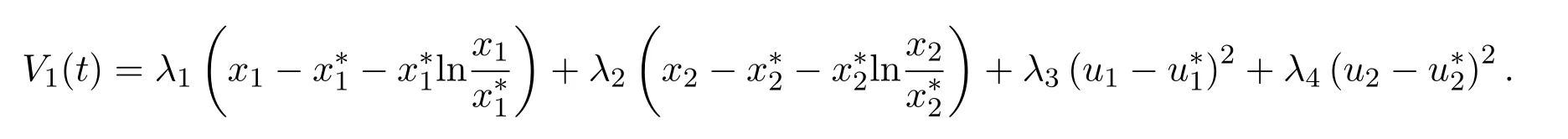
其中λi,i=1,2,3,4是待定正常数.沿着系统(1.3)的正解计算V1(t)的导数,借助(2.1)可得:
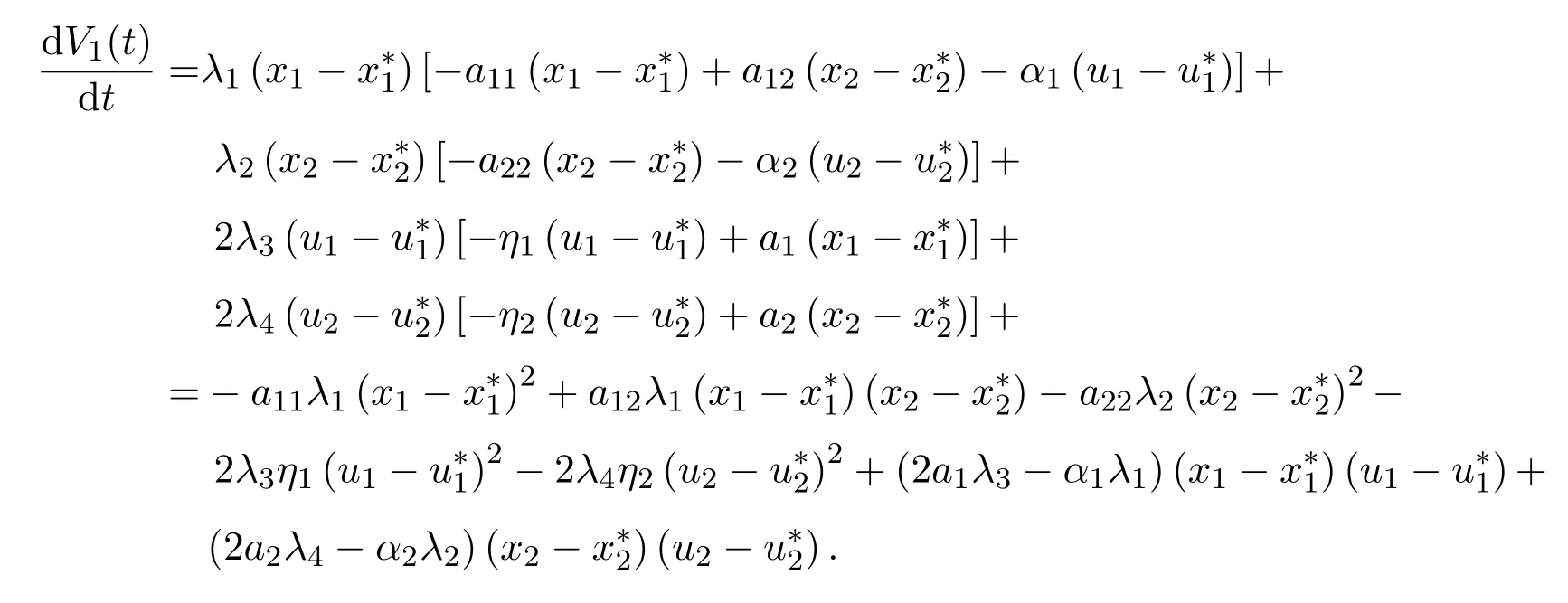
令
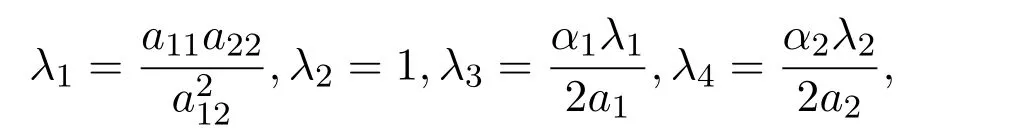
则有
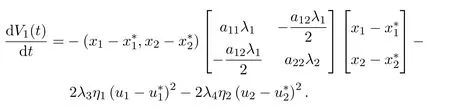
因为a11λ1>0,
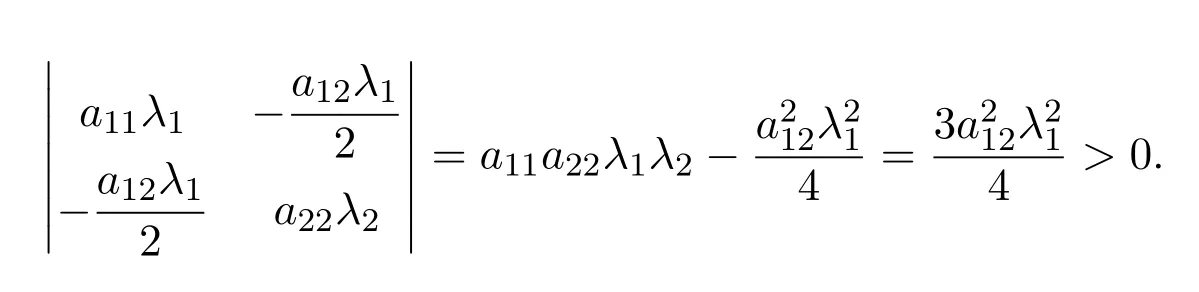
所以矩阵
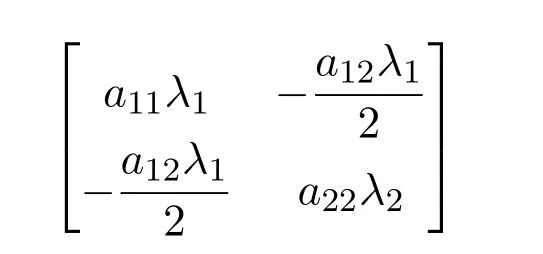
是正定矩阵.
这表明
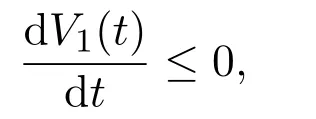
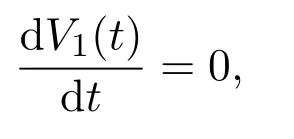
则由文献 [7]的 Lyapunov稳定性定理可知,正平衡点是全局渐近稳定的.
注 2.1定理2.1表明对于一方不能独立生存的偏利合作系统而言,在原系统(1.1)具有唯一的全局渐近稳定的正平衡点的情况下,反馈控制变量仅改变正平衡点的位置,使得种群的平衡密度发生改变,而不会改变正平衡点的稳定性.
定理 2.2若
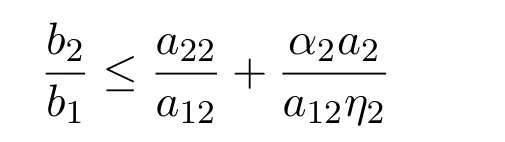
证明注意到满足:

现构造Lyapunov函数:
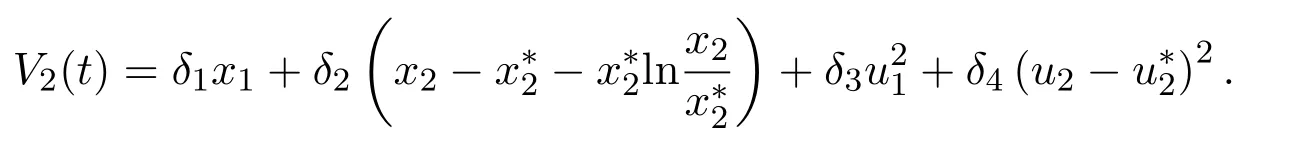
其中δi,i=1,2,3,4是待定正常数.沿着系统(1.3)的正解计算V2(t)的导数,借助(2.2)可得:
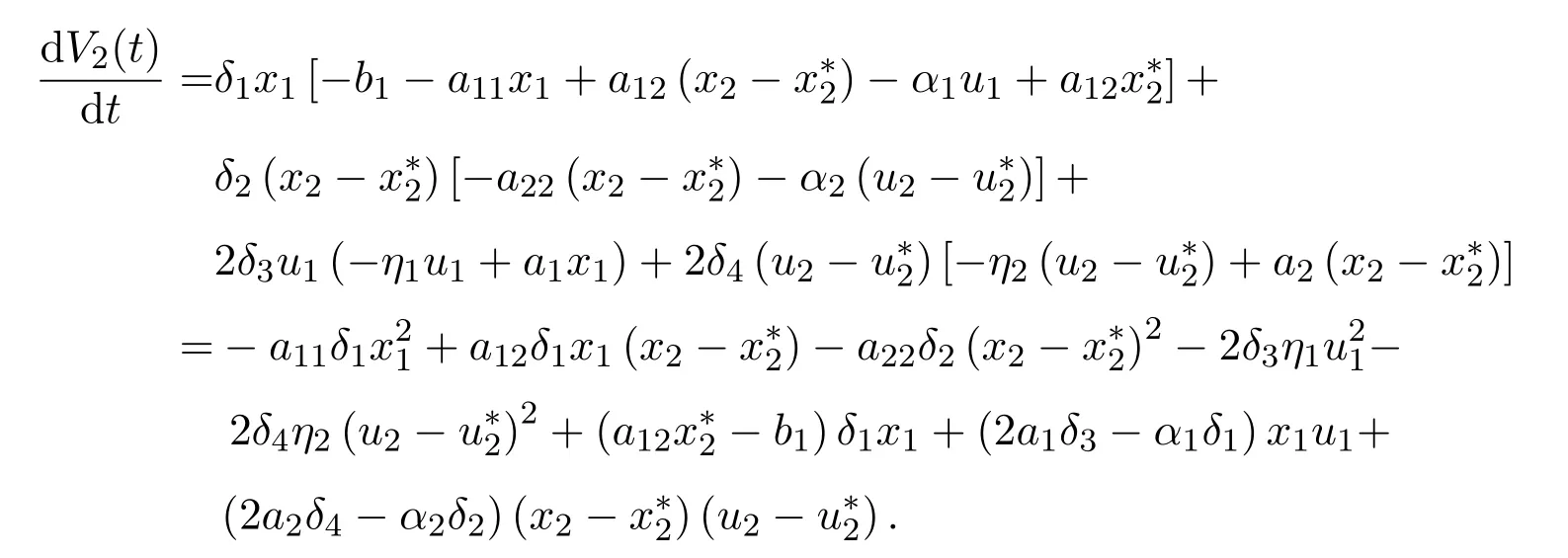
令
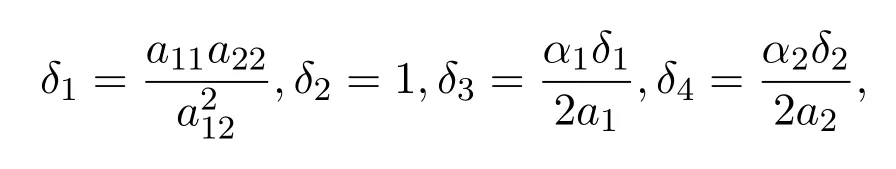
则有
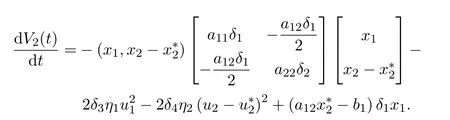
因为a11δ1>0,
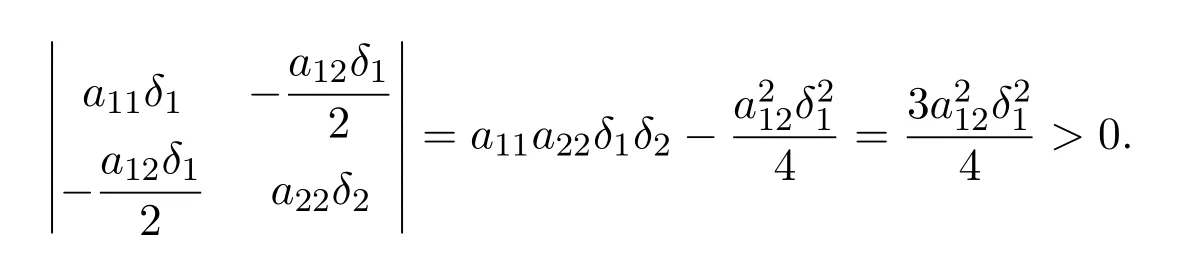
所以矩阵
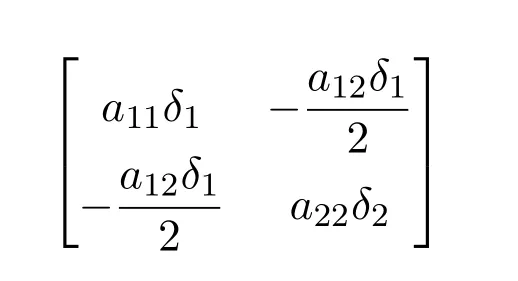
是正定矩阵.
又因为当
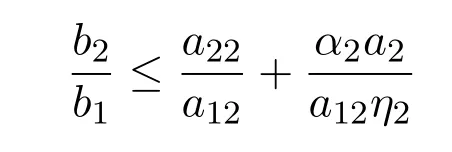
时,
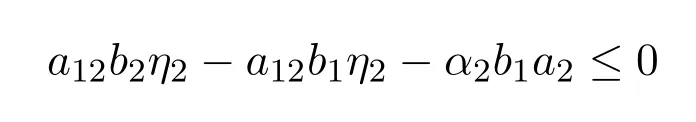
成立.所以
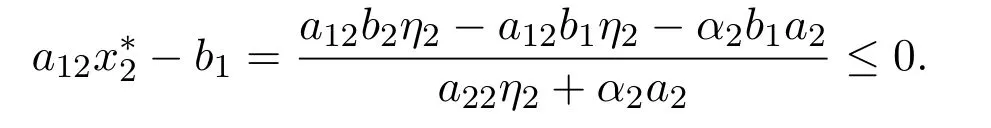
这表明
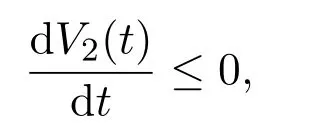
当且仅当x1=0,x2=x∗2,u1=0,u2=u∗2时,
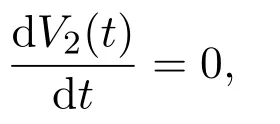
注 2.2当
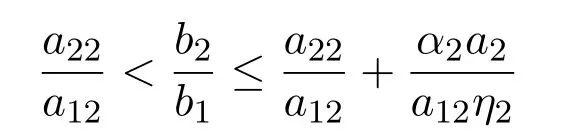
时,原系统(1.1)存在唯一的全局渐近稳定的正平衡点,但加入反馈控制变量后,系统(1.3)只存在唯一稳定的边界平衡点,这时不能独立生存的第一种群将最终走向灭绝.这表明不当的人类干扰反而不利于系统中生物种群的生长.
注 2.3值得注意的是,定理2.1和定理2.2的条件只含有跟第二个反馈控制变量u2有关的量a2和η2,而与u1无关.这说明第二个反馈控制变量u2影响系统(1.3)种群的生存,而第一个反馈控制变量u1与种群生存无关,仅影响种群的平衡密度.
3 数值模拟
以下通过具体的例子来验证定理的可行性.
例 3.1考虑如下系统:
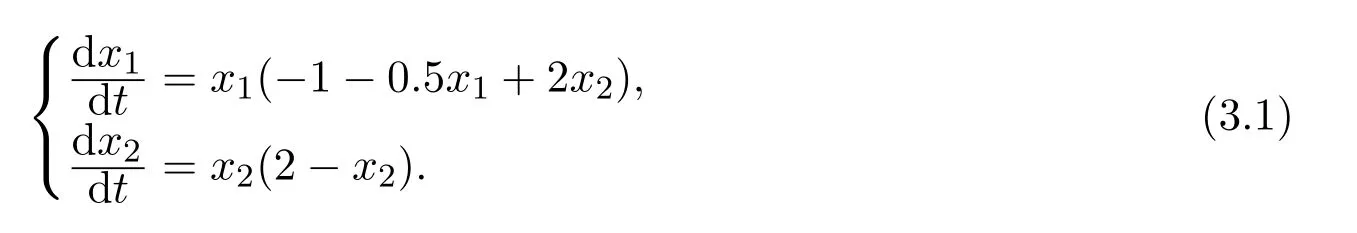
这里相对于系统(1.1),其中b1=1,b2=2,a11=0.5,a12=2,a22=1,则
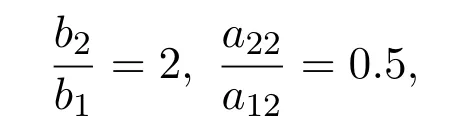
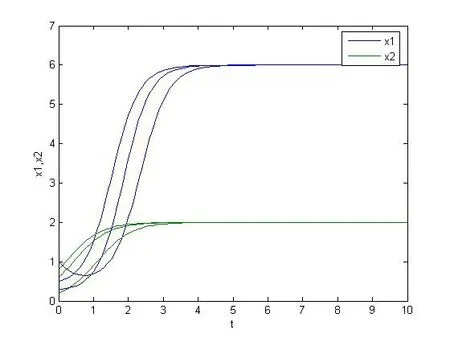
图1 系统(3.1)的数值模拟图
例 3.2考虑如下具有反馈控制变量的系统:
(1)满足定理2.1的实例
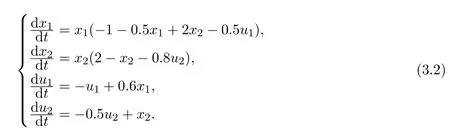
相对于例3.1,系统(3.2)增加系数
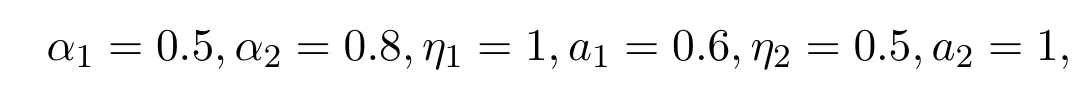
则
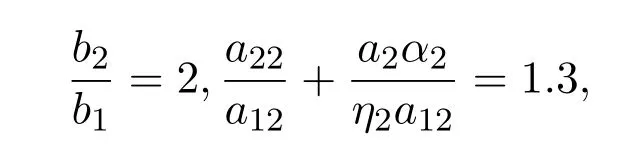
满足定理2.1的条件
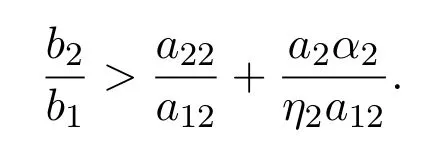
所以系统(3.2)存在唯一全局渐近稳定的正平衡点
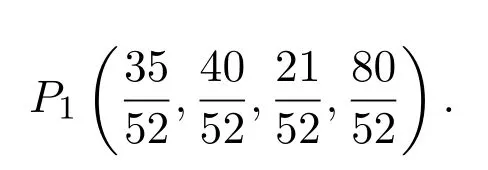
系统(3.2)具有初值
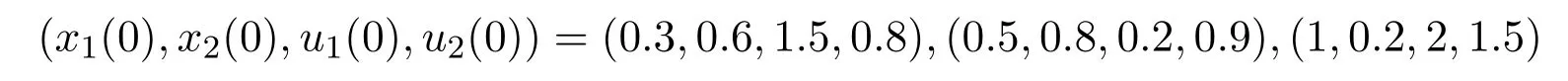
的解的数值模拟图,如图2所示:
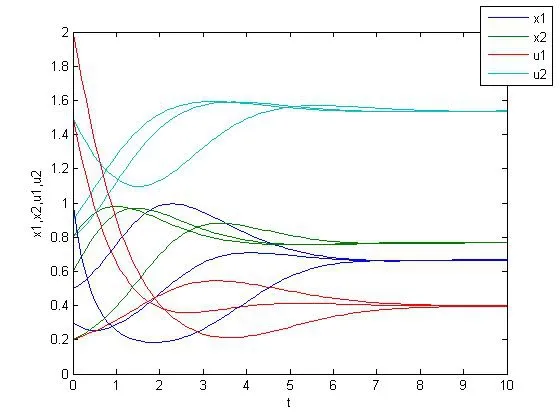
图2 系统(3.2)的数值模拟图
(2)满足定理2.2的实例
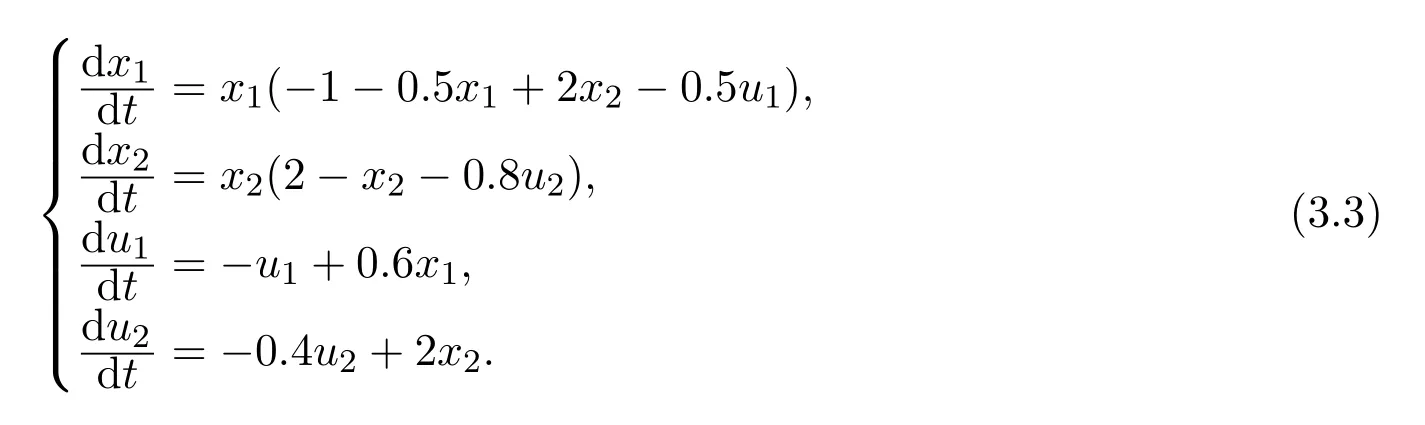
相对于系统(3.2),系统 (3.3)将η2和a2的值修改为η2=0.4,a2=2,则
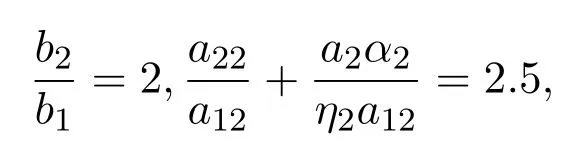
满足定理2.2的条件
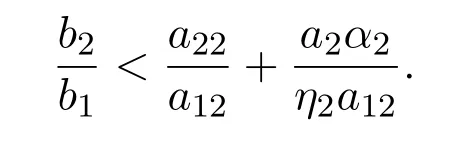
所以系统(3.2)存在全局渐近稳定的边界平衡点P2(0,0.4,0,2).系统(3.3)具有初值的解的数值模拟图,如图3所示:
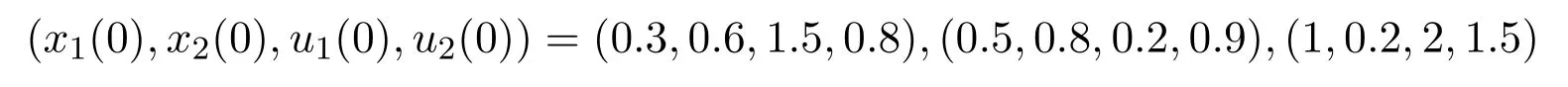
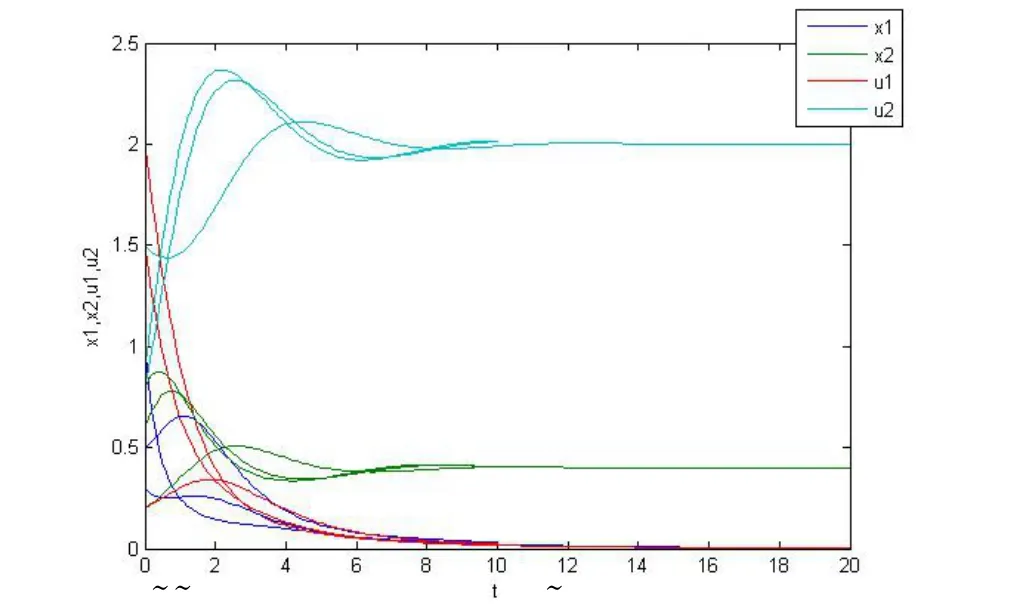
图3 系统(3.3)的数值模拟图
[1]赵亮,陈凤德.具有反馈控制的竞争系统边界平衡点的稳定性[J].北华大学学报,2013,14(5):516-519.
[2]杨坤,王海娜,陈凤德.反馈控制Lotka-Volterra合作系统稳定性研究[J].应用数学,2014,27(2):243-247.
[3]陈凤德,龚晓杰,普丽琼,等.具有反馈控制的 Lotka-Volterra捕食 -食饵系统研究[J].生物数学学报,2015,30(2):328-332.
[4]黄宏韬,林锦贤.具有反馈控制变量的偏害模型稳定性研究[J].福州大学学报,2017,45(1):69-73.
[5]祝占法,粟永安,徐芳.具有偏利关系的Lotka-Volterra模型[J].重庆工学院学报(自然科学版),2007,21(10):59-62.
[6]周晓燕,普丽琼,薛亚龙,等.具反馈控制的单方不能独立生存合作系统稳定性研究 [J].应用数学学报,2016,39(2):298-305.
[7]陈兰荪,宋新宇,陆征一.数学生态学模型与研究方法[M].成都:四川科学技术出版社,2003.

