CR(n,1)中半环上格林关系的开同余

练利锋

(重庆第二师范学院数学与信息工程学院,重庆 400065)

1 引言及预备知识

设 (S,+,·)是 (2,2)-型代数,其中 “+” 和 “·” 是二元运算.称 (S,+,·)是半环,若S满足:

(1)(S,+)和 (S,·)是半群;

(2)(S,+,·)满足等式x(y+z)≈xy+xz和(x+y)z≈xz+yz.

设ρ是半环(S,+,·)上的等价关系.如果ρ还满足:

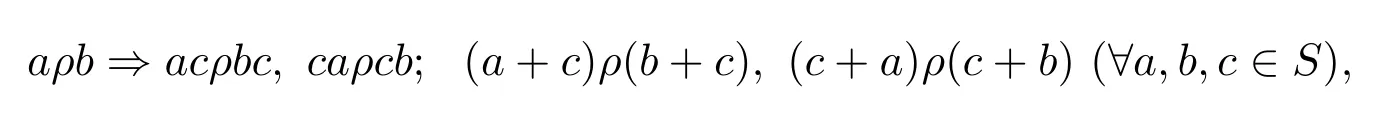
则称ρ是半环(S,+,·)上的同余关系.

半环可以看作是由分配律联系着的同一非空集合上的两个半群,因此,从半环的加法半群或乘法半群出发是研究半环的一种思路.格林关系在半群理论发展过程中扮演着非常重要的角色,而半环的乘法半群和加法半群都有各自的格林关系,将(S,+)上的格林L(R,D)关系记为上的格林L(R,D)关系记为因此对半环的乘法半群和加法半群的格林关系的研究是有意义的.许多代数学者对半群(半环)上的格林关系进行了研究.例如:文献[1]对半群上的格林关系进行了研究,文献[2]对完全正则半群上的格林关系进行了研究,文献[3]研究了幂等元半环的乘法班群上的格林D关系,文献[4]主要研究了幂等元半环上的格林L关系,文献[5-11]主要对幂等元半环上及其相关半环上的格林关系进行了刻画,得到了一些有趣的结论.然而,大多数情况下,格林关系并不是同余关系,但我们发现用格林关系的开同余代替同余关系本身更加方便.

设S是半环,若S满足恒等式:

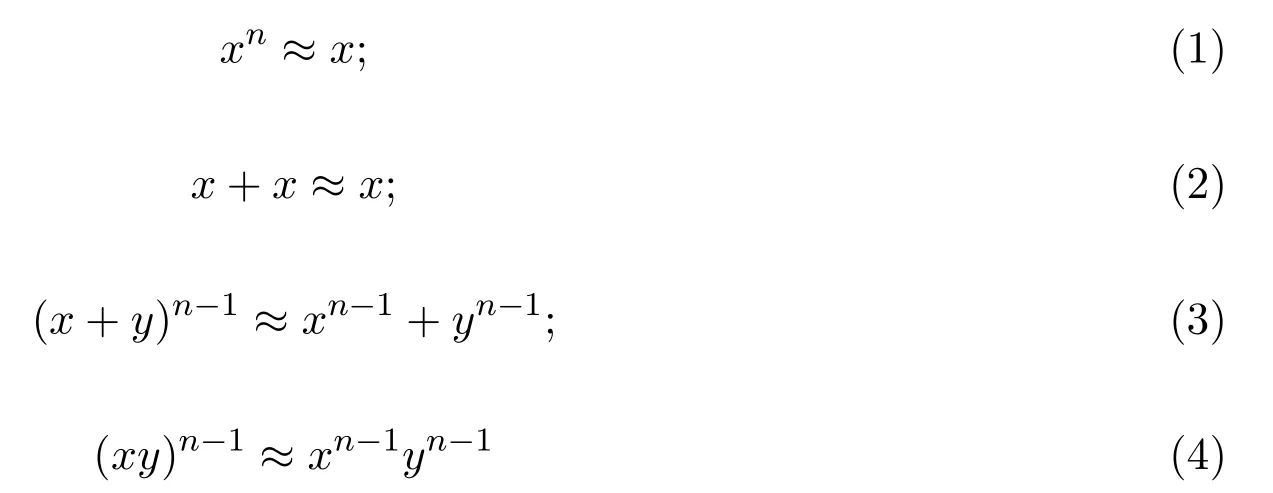
则对任意的a∈S,由aan−2a=a且aan−2=an−1=an−1a可知 (S,·)是完全正则半群.因此将满足(1),(2),(3)这三个附加恒等式的所有半环作成的簇记为CR(n,1).

设S是半环,ρ为S上的等价关系.用ρ⊕表示包还在ρ中的(S,+)上最大的同余关系,称其为由ρ确定的(S,+)上的开同余.类似的,由ρ确定的(S,·)上的开同余记为ρ⊙.由文献 [6]可知,

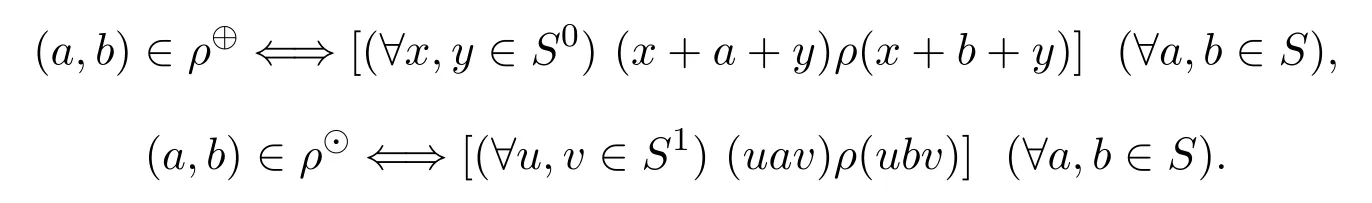
尽管ρ⊕和ρ⊙是半群 (S,+)与 (S,·)上的同余关系,但它们并不是半环(S,+,·)上的同余关系.称ρ⊕为加法开同余,ρ⊙为乘法开同余.并称(S,+,·)上的包含在ρ中的最大的同余关系为S上的开同余,记为ρ◦.

设S∈CR(n,1).则由文献[1]易得(S,+)和(S,·)上的和可分别表示为:

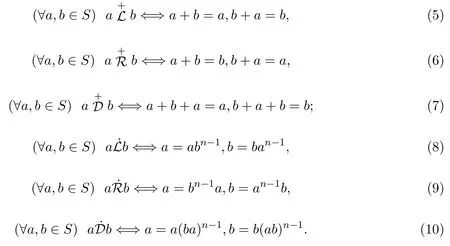
本文主要研究半环类CR(n,1)上格林关系的同余,并得到了一些有趣的结论.

2 CR(n,1)中半环上格林关系的开同余

引理 2.1[9]设ρ为半环S上的等价关系,则ρ的开同余ρ◦为ρ◦=(ρ⊕)⊙,或等价的有

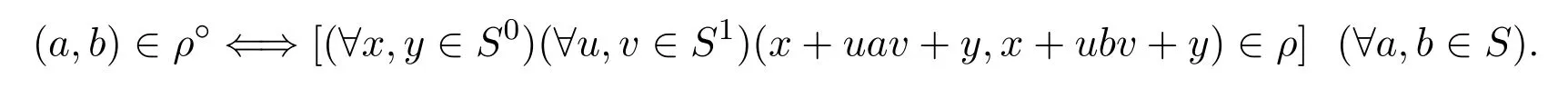
下面主要考虑半环类CR(n,1)中半环上的一些特殊的开同余,也就是半环上格林关系的开同余.

由文献[1]可知,对于任意半环(S,+,·),是(S,+)上的右同余,是(S,+)上的左同余,且与都是(S,·)上的同余关系.同样,文献[8]证明了是半环S上的同余关系.因此,它们的开同余可表示成下面的简单形式.

引理 2.2设(S,+,·)∈CR(n,1),则与可简单的表示为:

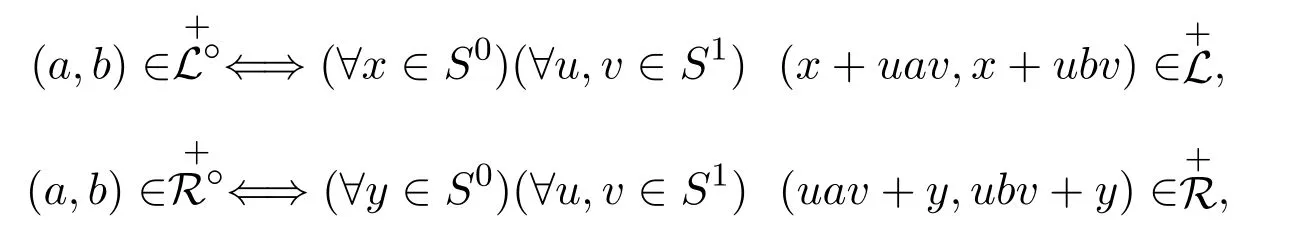
∀a,b∈ S.

引理 2.3设 (S,+,·)∈CR(n,1),则∀a,b∈S,有

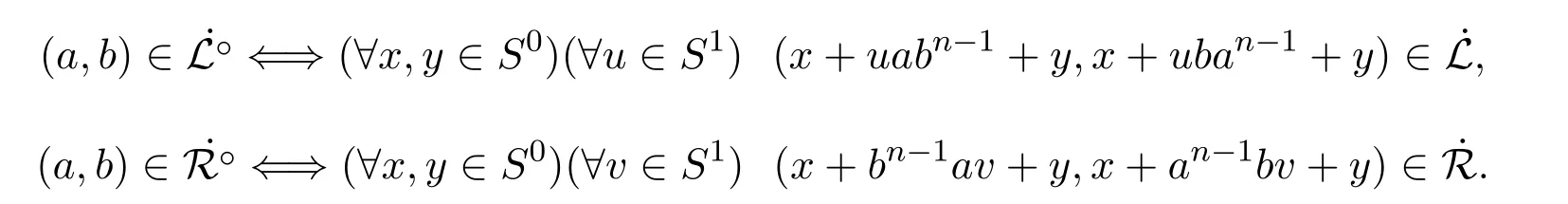
定理 2.1设S,T为任意半环,φ:S→T为满同态,则且a,b∈S.若在S中 (a,b)∈S,则在T中 (aφ,bφ)∈T.

证明我们只证明类似可证.为了方便设0φ=0,1φ=1.

设在S中,则

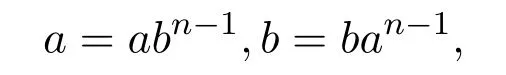
于是

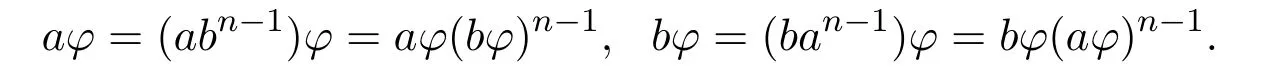
从而可知在T中有 (aφ,bφ)∈χ.

设(a,b)∈˙L◦,对于任意的p,q∈T0,r1,r2∈T1.存在x,y∈S0,u,v∈S1,使得

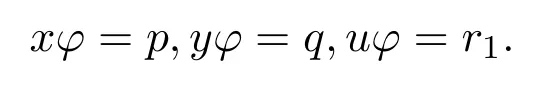
已知在S中,

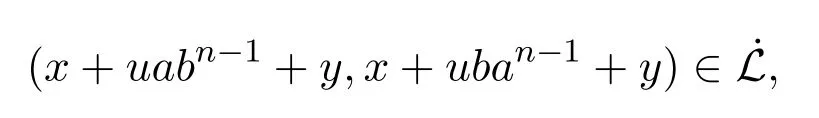
而由φ是同态映射可知,在T中,

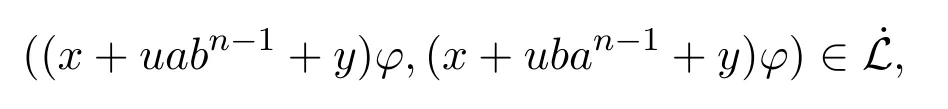
即

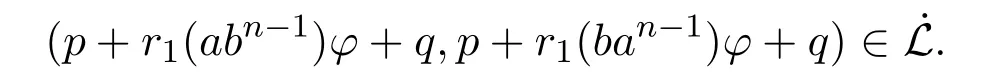
因此在T中,

文献[8]利用半环S的加法半群(S,+)上的格林关系的开同余给出了半环左、右约简的概念,类似的,我们也可以借助半环的乘法半群(S,·)上的格林关系的开同余定义半环的左、右约简.

定义 2.1如果是半环S上的恒等关系,则称S为左约简的,对偶的,如果是半环S上的恒等关系,则称S为右约简的.

定理 2.2设(S,+,·)∈CR(n,1),则分别是左、右约简的.

证明设且φ:S→T为自然同态映射,令0φ=0,1φ=1.

设∀a,b∈S,使得在T中满足由于为半环T上的同余关系,因此对于任意的x,y∈S0,u∈S1且

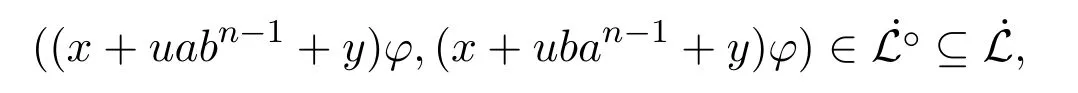
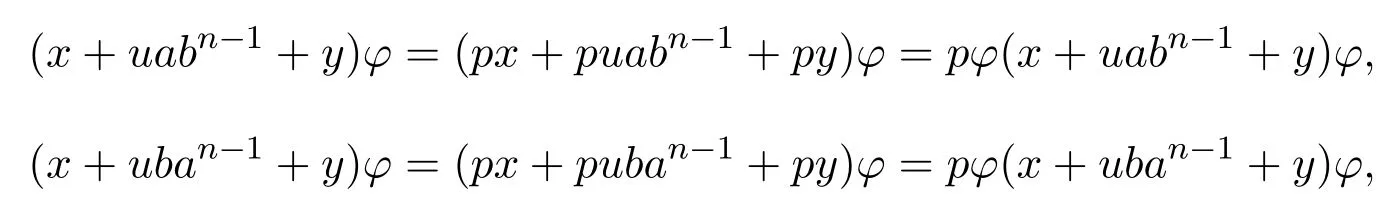
于是可得

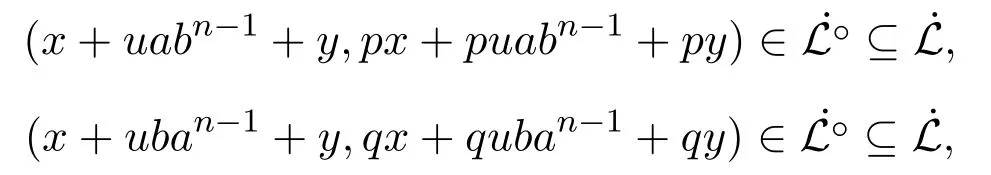
因此存在r1,r2∈S1,使得

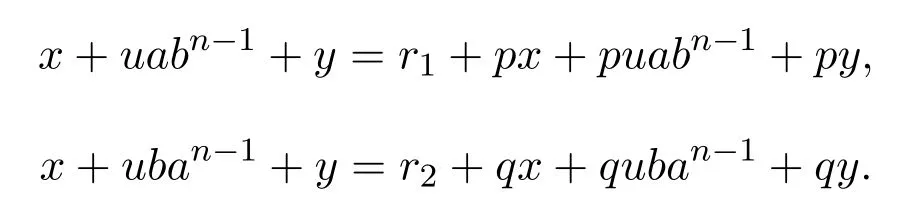
从而可知

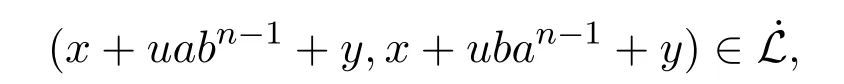
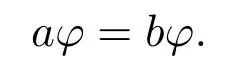
[1]Petrich M,Reilly N R.Completely Regular Semigroup[M].New York:Wiley,1999.

[2]Howie J M.Fundamentals of Semigroup Theory[M].Oxford:Oxford Science Publication,1995.

[3]Burris S,Sankppanaver H P.A Course in Universal Algebra[M].New York:Springer Verlag,1981.

[4]Pastijn F,Zhao X Z.Green′sD-relation for the multiplicative reduct of an idempotent semiring[J].Arch.Math.(Brno),2000,36:77-93.

[5]Zhao X Z,Shum K P,Guo Y Q.L-subvarieties of the variety of idempotent semirings[J].Algebra Universalis,2001,46:75-96.

[6]Zhao X Z,Guo Y Q,Shum K P.D-subvarieties of the variety of idempotent semirings[J].Algebra Colloquium,2002,9:15-28.

[7]Zhao X Z.Idempotent semirings with a commutative additive reduct[J].Semigroup Forum.,2002,64:289-296.

[8]Pastijn F,Zhao X Z.Varieties of idempotent semirings with commutative addition[J].Algebra Universalis,2005,54:301-321.

[9]Damljanović N,Ćirićv M,Bogdanović S.Congruence openings of additive Green′s relations on a semiring[J].Semigroup Forum.,2011,82(3):437-454.

[10]练利锋,任苗苗,陈益智.关于一类半环上的格林关系的若干研究[J].纯粹数学与应用数学,2014,30(5):420-427.

[11]秦官伟,任苗苗,邵勇.关于半环上格林关系的开同余[J].纯粹数学与应用数学,2012,28(5):668-675.